P5666 树的重心题解

P5666 树的重心：

M 分析暴力：

很容易打出一个 \(O(n)\)枚举边 再 \(O(n)\) 求重心 的\(O(n^2)\)的算法

期望得分：40 points

D 直接正解：

（其实分析链和完美二叉树可以与暴力一共拿到75分）

正解：整体复杂度\(O(n log n)\)

给出结论：

结论：一棵以 x 为根的树的重心，一定在 x 的重儿子所构成的集合中，而所有重儿子就构成了一条重链，

所以整个结论就是：一棵以 x 为根的树的重心，一定在 x 向下的重链上

因为整棵树是长这样的：（重链用绿色标出）

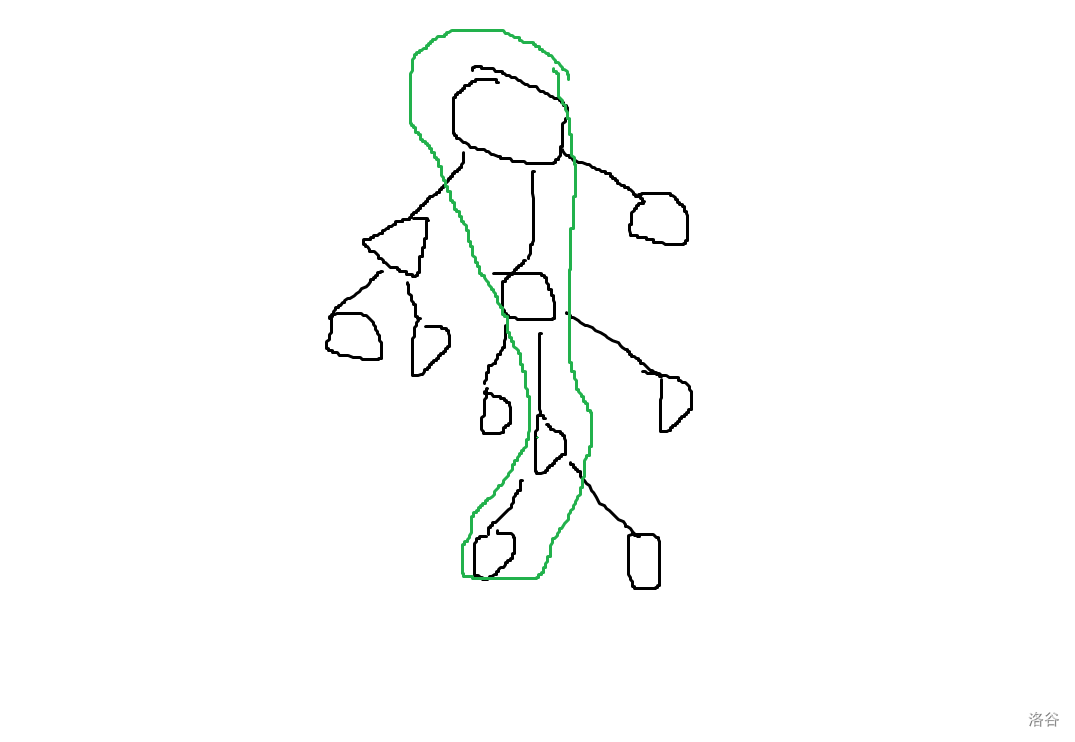
首先对于这条重链上的结点，它的子树珂以分为两类，

一个是它本身的儿子，一个是往父亲走的儿子，

第一类的子树size本身珂以处理出来

第二类的子树size 珂以用 size[root]-size[x]算出，

因为关注重心只用关注最大的子树，因为一类size是从 叶子->root 递增的，二类 size是从 叶子->root递减的

所以考虑倍增处理

设一个状态 \(f[x][t]\) 为 重链上的结点 x 向下走 \(2^t\) 步 珂以到达的结点

从大到小枚举 t 向下跳就好了，

考虑拥有两个重心的情况，首先这两个重心一定是相邻的(受到链和完美二叉树数据的启发得出的结论），所以只需要跑到最下面的重心判断他的fa就好了

然后对于每个结点的每一条出边跑一次\(O(logn)\)的倍增答案判定就好了

因为在代码中我们规定了一个根节点 1 ，那么我们在从上到下扫描出边的时候，每一条出边的终点其实就是它在这个有根树下的儿子，这个儿子如果删掉了它的父亲，它的重链是不会改变的所以可以直接倍增统计，

而对于它的父结点：

会分两种情况：

第一种断开了重链会改变，显然断开的是它的重儿子，那么断开后的重链显然是它的次重链。

第二种不变就可以直接统计了。

Code:

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=3e5+10,LOGN=20;
int n,siz[N],f[N][LOGN],son[N],fa[N];
ll ans;
int T,head[N],to[N<<1],Next[N<<1],tot;
inline int read(){
  int x=0,f=1;char ch=getchar();
  while(!isdigit(ch)){if(ch=='-'){f=-1;}ch=getchar();}
  while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch-'0');ch=getchar();}
  return x*f;
}
inline void add(int u,int v){
  to[++tot]=v,Next[tot]=head[u];
  head[u]=tot;
}
inline void get_son(int x) {for(int i=1;i<LOGN;++i) f[x][i]=f[f[x][i-1]][i-1];}
inline void calculate(int x){
  int u=x;for(int i=LOGN-1;i>=0;--i){if(f[u][i]&&siz[f[u][i]]*2>=siz[x]) u=f[u][i];}
  if(siz[u]*2==siz[x]) ans+=fa[u];//统计两个重心的情况
  ans+=u;
  return;
}
inline void dfs(int x,int ff) {
  fa[x]=ff;siz[x]=1;
  for(int i=head[x];i;i=Next[i]){
    int y=to[i];
    if(y!=ff){
      dfs(y,x),siz[x]+=siz[y];
      if(siz[y]>siz[son[x]]) son[x]=y;
    }
  }
  f[x][0]=son[x];get_son(x);
}
inline void getans(int x,int ff) {
  int x1=0,x2=0; siz[0]=0;
  for(int i=head[x];i;i=Next[i]){
    int v=to[i];
    if(siz[v]>=siz[x1]) x2=x1,x1=v;
    else if(siz[v]>=siz[x2]) x2=v;//找出重儿子和次重儿子
  }
  for(int i=head[x];i;i=Next[i]){
    int v=to[i];
    if(v!=ff){
      calculate(v);//直接统计出点
      f[x][0]=v==x1?x2:x1,get_son(x);
      //如果说断开的是重儿子，那么次重儿子一定就是新树的新重儿子
      //再重新更新重链结点
      siz[x]-=siz[v],siz[v]+=siz[x];//更新新树的size
      calculate(x);//统计 x 的答案
      fa[x]=v,getans(v,x);
      siz[v]-=siz[x],siz[x]+=siz[v];//还原答案
    }
  }
  f[x][0]=son[x];
  get_son(x),fa[x]=ff;
}
inline void myclear(){
	memset(siz,0,sizeof(siz));memset(son,0,sizeof(son));
	memset(f,0,sizeof(f));memset(fa,0,sizeof(fa));
	memset(head,0,sizeof(head));memset(to,0,sizeof(to));
	memset(Next,0,sizeof(Next));
}
int main() {
  T=read();
  while(T--){
    tot=0;
  	myclear();
    ans=0;n=read();
    for(int i=1,u,v;i<n;++i) {
      u=read(),v=read();
      add(u,v);
      add(v,u);
    }
    dfs(1,0),getans(1,0);
    printf("%lld\n",ans);
  }
  return 0;
}