针不辍的树链剖分(树剖入门)
针不辍的树链剖分
重链剖分
树链剖分 分为:重链剖分、长链剖分、实链剖分,一般说树链剖分指的是重链剖分。
(我也只会重链剖分和长链剖分)
这篇总结只讲解重链剖分 :(下面的图都是从教练哪里嫖的)
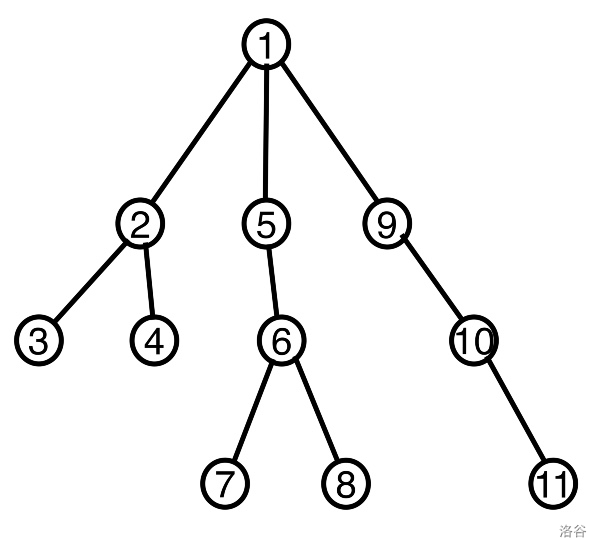
根据树的概念,树上存在着许多的链,
如本图中,就含有很多的链,
例如\(3-2-1-9-10-11\)就是其中一条链。
对于一棵树,如果我们已经找出了一条链,
除了维护整条链的操作是线性的此外,这条链周围点,也可以通过这条链实现快速的维护。
例如,还是上图中的\(3-2-1-9-10-11\)这一条链,当我们找出它时,便可以快速的维护\(4\)这个点(\(4\) 这个点向上一步就可以进入链中,复杂度也几乎属于常数)
所以总的来说,树链剖分 珂以减少树型结构的复杂度
将树形结构的玄学复杂度转化为了链的线性复杂度,这就是树链剖分的优秀之处
如何实现呢?
我们给出一些定义,并按以下规则划分割一颗树:
重子结点:一个结点的子节点中子数最大的结点
轻子节点:子节点中除了重子结点的都是轻子节点
从这个结点到重子节点的边为 重边 。
到其他轻子节点的边为 轻边 。
若干条首尾衔接的重边构成 重链 。
把落单的结点也当作重链,那么整棵树就被剖分成若干条重链
为了实现上面的步骤:
我们珂以使用两遍\(dfs\)来解决
第一遍 \(dfs\) 处理出每个结点的深度,父亲,子树大小
这是很简单的
当然你首先得确定一个根,这个根大部分时候都是随随便便就确定了,比如大部分时候我就取的\(1\)
接下来的操作就很简单了:
Code:
inline void dfs(int x,int f){
fa[x]=f;
dep[x]=dep[f]+1;
size[x]=1;
for(int i=head[x];i;i=Next[i]){
int y=to[i];
if(y!=f){
dfs(y,x);
size[x]+=size[y];
if(size[y]>size[son[x]]){
son[x]=y;
}
}
}
}
\(son[x]\)表示重子结点编号
\(size[x]\)表示\(x\)的子数大小
\(dep[x]\)表示\(x\)的深度
\(fa[x]\)表示\(x\)的父亲
第二次\(dfs\):
记录下每一条链的\(top\)或者说头结点 (\(top[x]\))?
以及访问所有结点的\(dfs\)序,使用数组\(dfn[x]\)记录
以及每一个\(dfs\)序所对应的结点\(rev[x]\)
inline void dfs2(int x){
if(son[fa[x]]!=x){
top[x]=x;
//它父亲的重儿子不是它,说明它在剖分后没有爹,单独成链
}
else{
top[x]=top[fa[x]];
//它是重儿子,top直接赋值就可以了,类似并查集的路径压缩
}
dfn[x]=++dnt;//dfs序的记录
rev[dnt]=x;//逆映射
if(son[x]){
//为了保证整条链的dfs序编号连续,优先访问重儿子
dfs2(son[x]);
}
for(int i=head[x];i;i=Next[i]){
int y=to[i];
if(y!=fa[x]&&y!=son[x]){
dfs2(y);
}
}
return;
}
使用针不辍的树链剖分优化LCA
对于很多的树上问题,都需要用到LCA,因为任意两个点有且仅有一条路径且一定经过它俩的LCA。所以,我们的树链剖分一定珂以优化LCA呀
对于这么一棵树
我们对它进行了两次\(dfs\)后
整课树会变成:
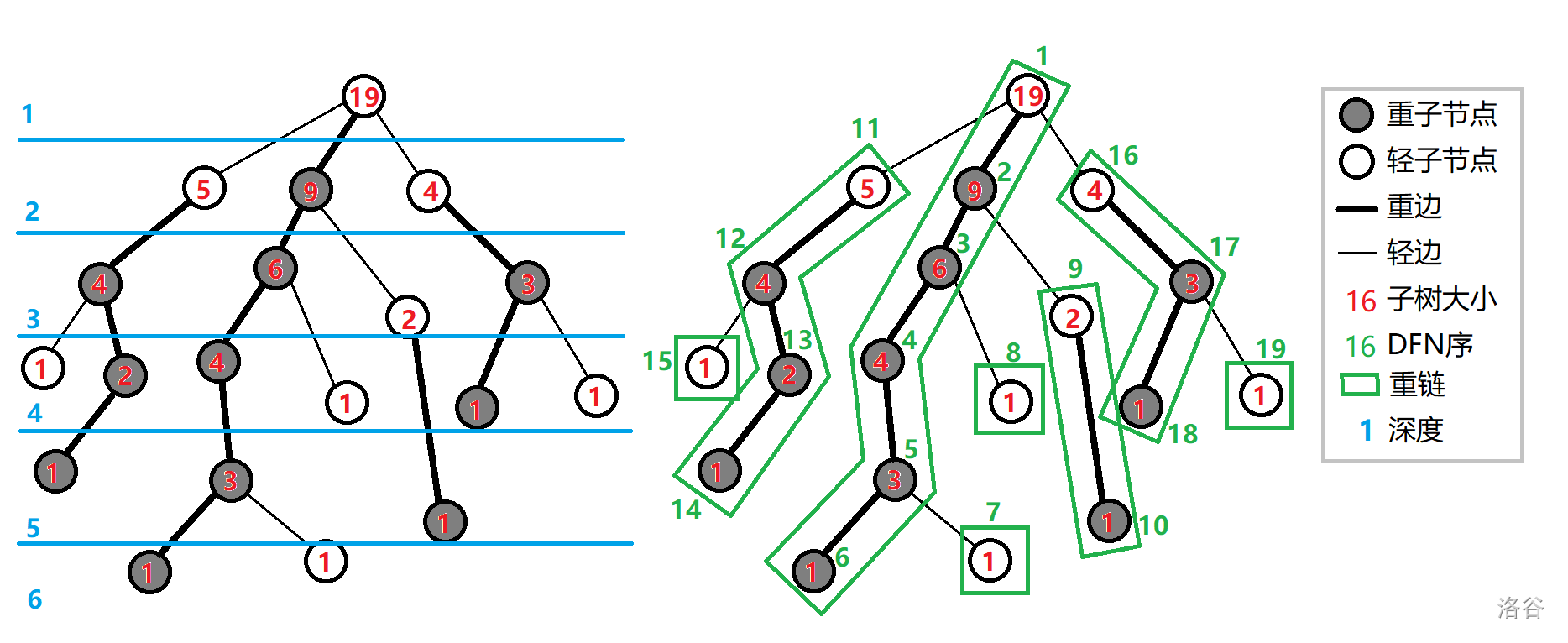
例如:(DFN序是绿色的)
我们要查找\(DFN\)序为 \(6\) 和 \(9\) 的LCA(假装\(6\)的真实编号为\(u\),\(9\) 的真实编号为\(v\) )
先查找 6 9 在不在同一条链中,在的话返回深度较小的结点
如何处理不在的情况呢?
仔细观察:
我们将 9 号结点调至整条链的top结点的父亲结点处(9本身就是它所在链的顶端)
这一次操作 9 -> 2
此时查找 6 2 是否在同一条结点
那么有人就要问了:
为什么不是选择跳 6 而是选择跳 9
6 的深度不是更低么?
首先这个图就是一个反例
6 这个链的顶端结点是根节点,而我们每次跳是会跳到每个链的\(top\)结点的父节点
找错答案暂且不论,甚至会出现\(u\) = 0 的情况
所以我们整个过程应该是这样的:(见注释)
inline int LCA(int u,int v){
while(top[u]!=top[v]){//不在同一条链中
if(dep[top[u]]>dep[top[v]]){//如果u所在链的顶端结点的深度小于v所在的,选择跳u
u=fa[top[u]];
}
else{
v=fa[top[v]];//否则选择跳v
}
}
return dep[u] > dep[v] ? v : u; //返回深度更小的结点,更上面的
}
尽量理解后自己打一遍后过一遍板子检查或者直接看下面例题AC代码中的树链剖分部分:
针不辍的树链剖分的板子题
大致介绍原理:
因为树链剖分后每一条链上的编号是连续的,所以节点保存的信息可以通过树状数组(前提是你会区间修改,)或者线段树维护。
(当然有一些可以树上差分的题用树状数组明显方便许多)
直接上板子题:
板子题一
题目给定了一棵树和所有的点权,要求求给定两个点的路径点权和 & 给定一个点的子树点权和。中途带修改
先考虑不带修改只有查询的情况:
对于任意两个点,它们两个的路径有且只有一条且一定经过它的\(LCA\),
我们先来看看求\(LCA\)的原代码:
inline int LCA(int u,int v){
while(top[u]!=top[v]){
if(dep[top[u]]>dep[top[v]]) u=fa[top[u]];
else v=fa[top[v]];
}
return dep[u]>dep[v] ? v : u;
}
整个\(LCA\)相当于我们在模拟求两个点\(LCA\)时点的跳动过程,
if(dep[top[u]]>dep[top[v]]) u=fa[top[u]];
else v=fa[top[v]];
这两行代码相当于我们用了一个\(O(1)\)的\(top[x]\)直接完成了点的跳动:
如果用暴力的话是一个\(O(n)\)的模拟跳动的每一层,
那么:在暴力的中途,我们可以将沿途的点的点权都加上,这样就可以解决了。
暴力的思路出来了,自然就可以想到优化了:
线段树+树链剖分
之前说过,一条链上的\(dfn\)序编号是连续的,那么我们完全可以建立一个线段树维护所有点的点权和。
此时,我们的\(dfn\)数组和\(rev\)逆映射数组又派上了用场:
在建树时,我们需要获取的是在这个\(dfn\)序上的点的点权:这个时候就要用到\(rev\)数组了。
建树代码:
struct seg_tree{
int l,r;
ll sum,lazy;
#define l(x) c[x].l
#define r(x) c[x].r
#define sum(x) c[x].sum
#define lazy(X) c[x].lazy
}c[800005];
inline void update(int x){sum(x)=(sum(lc)+sum(rc))%mod;}
inline void build(int x,int L,int R){
l(x)=L,r(x)=R;
if(L==R){
sum(x)=val[rev[L]]%mod;
return;
}
int mid=(L+R)>>1;
build(lc,L,mid);
build(rc,mid+1,R);
update(x);
}
而根据\(dfs2\)的代码来说,假设一个节点的\(dfn\)编号为\(x\),那么一个点的子树编号是在\([x,x+size[x]-1]\)之间的,所以说我们的\(4\)操作只需要\(query\)一次就行了
复杂度\(O(logn)\)
对于所有的 \(2\) 操作:
我们可以在\(LCA\)操作中添加几行\(query\)就行了
Code:
inline ll query_LCA(int u,int v){
ll ans=0;
while(top[u]!=top[v]){
if(dep[top[u]]>dep[top[v]]){
ans=(ans+query(1,dfn[top[u]],dfn[u]))%mod;
u=fa[top[u]];
}
else{
ans=(ans+query(1,dfn[top[v]],dfn[v]))%mod;
v=fa[top[v]];
}
}
if(dep[u]<dep[v]) swap(u,v);
ans=(ans+query(1,dfn[v],dfn[u]))%mod;
return ans;
}
考虑\(1\) , \(3\) 操作:
这不是呼之欲出了么?
\(1\) 操作 在求\(LCA\)位置的同时加一个修改操作不就好了么。。
3操作 修改子树跟查询一个道理呀。
这道题的坑点就在于对于\(long\) \(long\) 的取模了吧。。
Code
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define lc x<<1
#define rc x<<1|1
const int N=2e5+5;
inline int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-'){f=-1;}ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+(ch-'0');ch=getchar();}
return x*f;
}
inline ll read_LL(){
ll x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-'){f=-1;}ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+(ch-'0');ch=getchar();}
return x*f;
}
int head[N],tot,Next[N],to[N];
inline void add(int u,int v){
Next[++tot]=head[u];
head[u]=tot;
to[tot]=v;
}
int fa[N],dep[N],size[N],son[N],dfn[N],rev[N],dnt,top[N];
ll val[N];
ll mod;
inline void dfs1(int x,int f){
fa[x]=f,dep[x]=dep[f]+1;
size[x]=1;
for(int i=head[x];i;i=Next[i]){
int y=to[i];
if(y!=f){
dfs1(y,x);
size[x]+=size[y];
if(size[y]>size[son[x]]){
son[x]=y;
}
}
}
return;
}
inline void dfs2(int x){
if(son[fa[x]]!=x){top[x]=x;}
else{top[x]=top[fa[x]];}
dfn[x]=++dnt;
rev[dnt]=x;
if(son[x]){dfs2(son[x]);}
for(int i=head[x];i;i=Next[i]){
int y=to[i];
if(y!=fa[x]&&y!=son[x]){dfs2(y);}
}
}
struct seg_tree{
int l,r;
ll sum,lazy;
#define l(x) c[x].l
#define r(x) c[x].r
#define sum(x) c[x].sum
#define lazy(X) c[x].lazy
}c[800005];
inline void update(int x){sum(x)=(sum(lc)+sum(rc))%mod;}
inline void build(int x,int L,int R){
l(x)=L,r(x)=R;
if(L==R){
sum(x)=val[rev[L]]%mod;
return;
}
int mid=(L+R)>>1;
build(lc,L,mid);
build(rc,mid+1,R);
update(x);
}
inline void change(int x,ll d){
sum(x)=(sum(x)+(r(x)-l(x)+1)*d)%mod;
lazy(x)=(lazy(x)+d)%mod;
return;
}
inline void push_down(int x){
if(lazy(x)){
change(lc,lazy(x));
change(rc,lazy(x));
lazy(x)=0;
}
return;
}
inline void modify(int x,int L,int R,ll d){
if(l(x)>=L&&r(x)<=R){
change(x,d);
return;
}
push_down(x);
int mid=(l(x)+r(x))>>1;
if(mid>=L){modify(lc,L,R,d);}
if(mid<R){modify(rc,L,R,d);}
update(x);
return;
}
inline ll query(int x,int L,int R){
if(l(x)>=L&&r(x)<=R){return sum(x);}
push_down(x);
int mid=(l(x)+r(x))>>1;
ll ans=0;
if(mid>=L){ans=(ans+query(lc,L,R))%mod;}
if(mid<R){ans=(ans+query(rc,L,R))%mod;}
return ans;
}
inline void modify_LCA(int u,int v,ll d){
while(top[u]!=top[v]){
if(dep[top[u]]>dep[top[v]]){
modify(1,dfn[top[u]],dfn[u],d);
u=fa[top[u]];
}
else{
modify(1,dfn[top[v]],dfn[v],d);
v=fa[top[v]];
}
}
if(dep[u]<dep[v]) swap(u,v);
modify(1,dfn[v],dfn[u],d);
return;
}
inline ll query_LCA(int u,int v){
ll ans=0;
while(top[u]!=top[v]){
if(dep[top[u]]>dep[top[v]]){
ans=(ans+query(1,dfn[top[u]],dfn[u]))%mod;
u=fa[top[u]];
}
else{
ans=(ans+query(1,dfn[top[v]],dfn[v]))%mod;
v=fa[top[v]];
}
}
if(dep[u]<dep[v]) swap(u,v);
ans=(ans+query(1,dfn[v],dfn[u]))%mod;
return ans;
}
int n,m,root;
int main(){
n=read(),m=read(),root=read();
mod=read_LL();
for(int i=1;i<=n;++i){val[i]=read_LL();}
int u,v;
for(int i=1;i<n;++i){
u=read(),v=read();
add(u,v);
add(v,u);
}
dfs1(root,0);
dfs2(root);
build(1,1,n);
int op,x,y;
ll z;
while(m--){
op=read();
if(op==1){
x=read(),y=read();
z=read_LL();
modify_LCA(x,y,z);
}
else if(op==2){
x=read(),y=read();
printf("%lld\n",query_LCA(x,y));
}
else if(op==3){
x=read();
z=read_LL();
modify(1,dfn[x],dfn[x]+size[x]-1,z);
}
else{
x=read();
printf("%lld\n",query(1,dfn[x],dfn[x]+size[x]-1));
}
}
return 0;
}
板子题二:
emm
这道题的代码过程其实还要比上面一道题简单一些。。。因为没有线段树的区间修改过程
这道题的本质上是要求一条路径上的最小边权的最大值
稍微动动脑筋就会想到应该先去掉一些无用的边,比如 \(1\) 这个点连接了 \(3\) 这个点,而 1 到 3 有两条边,一条边权为 4 一条边权为 5
肯定会选择边权为 5 的边,那么如何去掉那些边权小的边呢?
其实,转化一下也就等于 如何保留那些边权大的边
这句话是不是听起来很像最小生成树中的一个引理:
边权最小的边一定在最小生成树中
所以答案也就是先对整个图跑一遍最大生成树
这个时候整个图就是一棵树了,再用线段树维护区间最小值就行了
这道题只给了边权,不过问题不大,简单的边权转化为点权就行了
不过也有坑点:
并查集用了 fa 数组,而树链剖分中也会用到 fa 数组,记得区分就好了
Code:
#include<bits/stdc++.h>
using namespace std;
#define lc x<<1
#define rc x<<1|1
int n,m;
int q;
int fa_bingchaji[100005],fa[100005],size[100005],dep[100005];
bool vis[100005];
int a[10005],son[10005];
int val[10005];
inline int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-'){f=-1;}ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
return x*f;
}
inline int get(int x){return x==fa_bingchaji[x] ? x : fa_bingchaji[x]=get(fa_bingchaji[x]);}
inline void merge(int x,int y){fa_bingchaji[get(x)]=get(y);}
struct node{int x,y,w;}e[100005];
inline bool cmp(node o,node p){return o.w>p.w;}
int head[10005],Next[100005],to[100005],edge[100005],tot,cnt,dfn[100005];
int top[10005];
inline void add(int u,int v,int w){
edge[++tot]=w;
to[tot]=v;
Next[tot]=head[u];
head[u]=tot;
}
inline void dfs1(int x,int f){
dep[x]=dep[f]+1,fa[x]=f,size[x]=1;
for(int i=head[x];i;i=Next[i]){
int y=to[i];
if(y==f) continue;
a[y]=edge[i];
dfs1(y,x);
size[x]+=size[y];
if(size[y]>size[son[x]]){son[x]=y;}
}
}
inline void dfs2(int x){
if(son[fa[x]]!=x) top[x]=x;
else{top[x]=top[fa[x]];}
val[++cnt]=a[x];
dfn[x]=cnt;
if(son[x]){dfs2(son[x]);}
for(int i=head[x];i;i=Next[i]){
int y=to[i];
if(y==fa[x]||y==son[x]) continue;
dfs2(y);
}
}
struct seg_tree{
int l,r;
int minn;
seg_tree(){minn=0x3f3f3f3f;}
#define l(x) c[x].l
#define r(x) c[x].r
#define minn(x) c[x].minn
}c[40005];
inline void update(int x){minn(x)=min(minn(lc),minn(rc));}
inline void build(int x,int l,int r){
l(x)=l;r(x)=r;
if(l==r){
minn(x)=val[l];
return;
}
int mid=(l+r)>>1;
build(lc,l,mid);
build(rc,mid+1,r);
update(x);
return ;
}
inline void modify(int x,int go,int v){
if(l(x)==r(x)){
minn(x)=v;
return;
}
int mid=(l(x)+r(x))>>1;
if(mid>=go){modify(lc,go,v);}
else{modify(rc,go,v);}
update(x);
return;
}
inline int query(int x,int L,int R){
if(l(x)>=L&&r(x)<=R){return minn(x);}
int mid=(l(x)+r(x))>>1;
int ans=0x3f3f3f3f;
if(mid>=L){ans=min(ans,query(lc,L,R));}
if(mid<R){ans=min(ans,query(rc,L,R));}
return ans;
}
inline int LCA(int u,int v){
int ans=0x3f3f3f3f;
while(top[u]!=top[v]){
if(dep[top[u]]>dep[top[v]]){ans=min(ans,query(1,dfn[top[u]],dfn[u]));u=fa[top[u]];}
else{ans=min(query(1,dfn[top[v]],dfn[v]),ans);v=fa[top[v]];}
}
if (dep[u]<dep[v])swap(u,v);
ans=min(ans,query(1,dfn[v]+1,dfn[u]));
return ans;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;++i){scanf("%d%d%d",&e[i].x,&e[i].y,&e[i].w);}
sort(e+1,e+m+1,cmp);
for(int i=1;i<=n;++i){fa_bingchaji[i]=i;}
for(int i=1;i<=m;++i){
if(get(e[i].x)==get(e[i].y)){continue;}
add(e[i].x,e[i].y,e[i].w);
add(e[i].y,e[i].x,e[i].w);
merge(e[i].x,e[i].y);
}
dfs1(1,0);
dfs2(1);
build(1,1,n);
modify(1,1,0x3f3f3f3f);//因为root上没有点权,避免影响之后的查询最大值
scanf("%d",&q);
int x,y;
while(q--){
scanf("%d%d",&x,&y);
if(get(x)!=get(y)){puts("-1");continue;}
printf("%d\n",LCA(x,y));
}
return 0;
}
板子题三
这题题意有些绕,大致意思就是:
install:查找这个点到根的路径上有多少个 0,输出,再将所有 0 修改为 1
uninstall:查找这个点的子树有多少个 1 输出,再将所有 1 都修改为 0
根据这个题意珂以想到一个性质:就是一个区间如果包括在目标区间中,他的sum只能变为0或区间长度。
这不就是树链剖分版题了么。。。
懒标记分为两种一种为 install 操作,一种为 uninstall 操作
install 操作是从结点到根的,只需要对 LCA 代码做一些小小的修改就可以了:(seg就是dfn序)
inline int to_root_install(int u){
int ans=0;
while(top[u]!=1){
ans+=query(1,seg[top[u]],seg[u]);
modify(1,seg[top[u]],seg[u],1);
u=fa[top[u]];
}
ans+=query(1,1,seg[u]);
modify(1,1,seg[u],1);
return ans;//注意这个时候返回的是 1 的个数,我们需要用dep-ans才能得到答案
}
uninstall操作:这就一子树操作呀。。直接query \([seg[u],seg[u]+size[u]-1]\)就好了呀。。
然后再 \(modify[seg[u],seg[u]+size[u]-1]\)就行了
整个代码:
#include<bits/stdc++.h>
using namespace std;
#define lc x<<1
#define rc x<<1|1
const int N=1e5+5;
int head[N],Next[2*N],to[2*N],tot,n,q;
inline int read(){
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){
if(ch=='-'){f=-1;}ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
return x*f;
}
inline void add(int u,int v){
to[++tot]=v;
Next[tot]=head[u];
head[u]=tot;
}
int dep[N],fa[N],size[N],son[N];
inline void dfs1(int x,int f){
dep[x]=dep[f]+1;
size[x]=1;
fa[x]=f;
for(int i=head[x];i;i=Next[i]){
int y=to[i];
if(y!=f){
dfs1(y,x);
size[x]+=size[y];
if(size[y]>size[son[x]]){son[x]=y;}
}
}
}
int top[N],seg[N],rev[N],dnt;
inline void dfs2(int x){
if(son[fa[x]]!=x) top[x]=x;
else top[x]=top[fa[x]];
seg[x]=++dnt;
rev[dnt]=x;
if(son[x]){dfs2(son[x]);}
for(int i=head[x];i;i=Next[i]){
int y=to[i];
if(y!=fa[x]&&y!=son[x]){dfs2(y);}
}
}
//----------------------------------------树链剖分预处理
struct seg_tree{
int l,r;
int sum,lazy;
#define l(x) c[x].l
#define r(x) c[x].r
#define sum(x) c[x].sum
#define lazy(x) c[x].lazy
}c[4*N];
inline void update(int x){sum(x)=sum(lc)+sum(rc);}
inline void build(int x,int l,int r){
l(x)=l,r(x)=r;
if(l==r){
sum(x)=0;
lazy(x)=0;
return;
}
int mid=(l+r)>>1;
build(lc,l,mid);
build(rc,mid+1,r);
update(x);
}
//--------------------------------------所有的软件开始为未安装的
inline void change(int x,int d){
if(d==1){sum(x)=r(x)-l(x)+1;lazy(x)=1;}
else{sum(x)=0;lazy(x)=2;}
return;
}
//---------------------------------------1 表示安装 2 表示卸载
inline void push_down(int x){
if(lazy(x)){
change(lc,lazy(x));
change(rc,lazy(x));
lazy(x)=0;
}
}
inline void modify(int x,int L,int R,int d){
if(l(x)>=L&&r(x)<=R){
change(x,d);
return;
}
push_down(x);
int mid=(l(x)+r(x))>>1;
if(mid>=L){modify(lc,L,R,d);}
if(mid<R){modify(rc,L,R,d);}
update(x);
return;
}
inline int query(int x,int L,int R){
if(l(x)>=L&&r(x)<=R){return sum(x);}
push_down(x);
int mid=(l(x)+r(x))>>1;
int res=0;
if(mid>=L){res+=query(lc,L,R);}
if(mid<R){res+=query(rc,L,R);}
return res;
}
inline int to_root_install(int u){
int ans=0;
while(top[u]!=1){//root原本是0,但我将所有的编号都加了1
ans+=query(1,seg[top[u]],seg[u]);
modify(1,seg[top[u]],seg[u],1);
u=fa[top[u]];
}
ans+=query(1,1,seg[u]);
modify(1,1,seg[u],1);
return ans;
}
int main(){
n=read();
int tep;
for(int i=2;i<=n;++i){
tep=read();
add(tep+1,i);
add(i,tep+1);//编号都得加一,所以输入也从2开始
}
dfs1(1,0);
dfs2(1);
build(1,1,n);
q=read();
string op;
int u;
while(q--){
cin>>op;
u=read();
u+=1;
if(op=="install"){printf("%d\n",dep[u]-to_root_install(u));}
else{//普通操作
printf("%d\n",query(1,seg[u],seg[u]+size[u]-1));
modify(1,seg[u],seg[u]+size[u]-1,2);
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号