模拟赛 2
11.16
T2
先考虑前两个限制，发现都是与奇偶性相关的，考虑建二分图，在不考虑第三个限制下是一个最大独立集计数。
发现由于连边方式是每一位向相邻两位连边，那么最大独立集数一定是 \(\frac{n}{2}\)，并且一定形如先选一段奇数再选一段偶数的形式。
再考虑一下第三个限制，考虑对每个配对的 \((l,r)\) 加上一条 \(l\to r\) 的边，发现只有最外层括号的限制是有用的，因为内层括号的限制一定被外层括号的限制包含，那我们考虑枚举奇数和偶数的分界点，发现每个限制实际上就是形如区间 \([l,r)\) 不能选，我们考虑把左括号设为 \(1\) 右括号设为 \(-1\) 那么能选的 \(r\) 实际上就是前缀和为 \(0\) 的地方，上线段树维护即可。
T3
考虑没有包含关系是好做的，在离散化后你暴力修改覆盖区间是均摊 \(O(1)\) 的，考虑有了区间包含后一定优先选择被包含的区间，那我们考虑维护一个待选区间的集合，每次取出最小的区间后将包含他的且不被别的区间包含的区间加入即可。
比较简单的实现方法是拿线段树优化建图建出一个 DAG。
P11281
小猜一手结论有最后的合法状态肯定是形如 \(p_{p_i}=i\) 的，先把给定的限制加上，然后若干不确定的位，数量记为 \(m\)，再钦定若干位为 \(p_i=i\)，然后剩下的位置两两配对算方案数就行。
P11282
考虑按 \(pos\) 的奇偶性分类讨论。
对于 \(pos=1\lor pos=n\) 的数，不难发现在 \(n>3\) 时均有解。
对于偶数位，考虑先对 \([1,pos-1]\) 和 \([pos+1,n]\) 进行操作，那么最后肯定会剩下三个数，因为我们只在意首位两个数与 \(p_{pos}\) 的大小关系，所以我们只用关心极值就行，规定大于为 \(1\) 小于为 \(0\)，假如最后能有 \(11\) 或 \(00\) 的情况就是有解，否则无解。
对于奇数位，考虑同样按上面做，那么最后会剩下来五个数，我们还是只考虑和 \(p_{pos}\) 的大小关系，那么最后只有 \(0110,1001,0011,1100,0000,1111\) 六种状态是合法的，因为左右是对称的所以我们只考虑前两个数，对于这些合法的状态我们贪心的让他们尽量被取到，对于第二个数也就是紧贴 \(pos\) 的数，我们选择距离 \(pos\) 最近的 \(0/1\)，因为我们要让他保留下来所以对于 \([1,pos-1]\) 的前缀要分给他一个奇数长度的后缀，我们让这个后缀尽量小的前提下，对于剩下的那个前缀去选择他的极值留下来，这样的情况下选择的极值一定是最优的，然后将极值与 \(p_{pos}\) 比大小判定即可。
11.17
P5362
因为昨天晚上的 ABC D 题突然想起来这题还没做，过来补一下。
首先题中给的序列生成方式很神秘啊，显然不能直接做，需要转化一下，我这里直接给转化后的生成方式：
初始序列 \(\{T_0\}\) 为 \(0\)，每次将 \(0\to 01,1\to 10\) 迭代若干次得到 \(\{T_n\}\)。
这个划分方式就是对于相邻的两个元素分为一组，如果有相同的相邻两个元素就是非法，这样一共有两种划分方式，对应不同的起始位置（另外假如一个二元组只知道其中一个元素，不难发现另外一个元素也是唯一的）。
好处是可逆的，这就使得我们将给定的 \(S\) 倒着推到足够短后手玩就行。
加上 \(k\) 之后就带着 \(k\) 一起递归就行，注意每次假如结尾处只有一个元素被分为一组，需要占用 \(k\) 的一个位置。
AGC002E
首先按照 \(a_i\) 从大到小排个序，发现实际上就是每次选择消除一行或一列最后没得消的人输，进一步转化其实就是给你一个阶梯形状的网格图，每次向上或者向右走一格不能走的人输。
结论是每个点的状态和对角线上的状态一样，证明如下：
- 对于先手必败的点 \((x,y)\)，那么 \((x+1,y),(x,y+1)\) 一定必胜，那么对于 \((x+1,y+1)\) 必胜的情况，\((x+2,y),(x,y+2)\) 是先手必败，对应的 \((x+2,y+1),(x+1,y+2)\) 一定有一个是必败的，这显然与 \((x+2,y),(x,y+2)\) 是先手必败是相悖的。
- 对于先手必胜的点 \((x,y)\)，那么 \((x+1,y),(x,y+1)\) 至少有一个必败，对应的 \((x+1,y+1)\) 就是必胜的。
那么找出与 \((0,0)\) 在同一对角线上的最远点，然后依据到边界距离的奇偶性判断即可。
P5008
先考虑 DAG 的情况，容易发现除了没有入度的点其他的点都能选。
对于没有单独的自环的强连通分量来说，肯定是可以以每个点作为起点然后走反向边消到只剩一个点的，如果有自环那就以自环的点为起点就行。
那么考虑对原图缩点，对于新图上入度为 \(0\) 且无自环点的强连通来说，贪心的不选最小值，其他的强连通都是可选的。
P11291
学生奋战一晚上终于战胜。
先考虑 \(O(k|T|)\) 的暴力做法，对于每个 \(i\) 把他当成 \(l\) 每次往右跳一步并统计贡献。
把当前造成贡献的区间看成一个节点，然后跳一步看成连一条边容易发现这是一棵内向树，那么刚才的过程相当于树上倍增，然后对树链加一个等差数列。
对于这种等差数列的问题，考虑给他拆成和深度有关的一次函数的形式，那么第一问是简单的。
对于第二问，考虑贡献有祖先对自己的和自己对自己的贡献，祖先对自己的贡献，可以通过树上前缀和算出来，自己对自己的贡献，考虑再对序列上的每个位置的答案维护一个和下标有关的一次函数，差分即可。
细节很多。
11.20
T1
好像我的做法麻烦了不少。
其实就是贪心的模拟，我这里使用 set。
考虑统计一下每个 \(i\) 对应属于哪两个堆，对于每个堆维护两个指针，一个维护从上方取到哪了，一个维护从下方取到哪了，对应的对于每个 \(i\) 记录一下能否被从上面取到或者从下面取到，每次更新 \(O(1)\) 个 \(i\)，复杂度是 \(O(n\log n)\) 的，实现较为复杂。
T2
签到题。
对于非环边，枚举断或者不断，然后对于环上的点进行一个双指针的扫。
T3
dp of dp
考虑枚举最终 s 的状态，设 \(f_{i,j}\) 表示 s 考虑到第 \(i\) 位，s2 考虑到第 \(j\) 的情况，有：
发现 s2 的长度十分小考虑把 \(f_i\) 状压起来 DP，设 \(g_{i,S}\) 表示 s 考虑到第 \(i\) 位，匹配状态为 \(S\) 的方案数。
T4
哎不是这咋就有凸性了。
我们令 \(f_i\) 为选了 \(i\) 条线段全覆盖的最小花费，根据人类智慧这玩意是凸的，所以考虑 WQS 二分。
我们考虑二分一个加权 \(mid\) 让所有区间的权值减去他，然后显然代价非负的区间是全选的，但是会有一些没有覆盖。
我们对于每个 \(i\) 记录一下右端点为 \(i\) 的最远左端点 \(pos_i\)，然后考虑设 \(dp_i\) 表示 \([1,i]\) 全被覆盖的最大代价，那么对于 \(i\in [pos_i,i-1]\) 肯定是直接取 \(\max\)，对于 \([1,pos_i-1]\) 实际要多选的就是一个前缀 \(\min\)，这两部分都能拿树状数组实现。
11.21
T1
考虑维护一个未匹配栈，每次和栈顶匹配，发现相同栈顶对应栈内状态是一样的，考虑对每个栈顶维护一个集合存有哪些位置消到了栈顶。
那么答案只会在相同集合产生贡献，而且贡献的形式形如一个后缀和差分的形式，可以轻松维护。
需要开 \(10^7\) 个 vector 卡常也卡空间。
T2
原神。
最终答案的贡献是形如 \((sum_i-sum_j)\times 10^{-(n-i)}\equiv 0\pmod d\)，其中 \(sum_i=\sum_{j=1}^i s_i\times 10^{n-i}\)。
考虑把 \(d\) 拆成 \(2^x5^ym\) 的形式，那么在 \(j\le i-20\) 时一定有 \(sum_i\equiv 0\pmod{2^x5^y}\)，所以只用考虑和 \(10\) 互质的 \(m\) 即可直接开桶记录就行。
对于 \(j>i-20\) 的部分直接暴力即可。
T3
考虑钦定本质不同的情况只有在第一次出现时才被计数，并且发现方案数重复只会发生在一个颜色连续段内，所以考虑维护一个 \(f_{i,j}\) 表示相对于连续段上一个位置 \(j-1\) 的新增本质不同方案数，以及一个 \(d_{i,j}\) 表示相对于连续段上一个位置有多少多少方案数不能取到。
考虑转移这个东西，考虑填表。
对于连续段上的一个位置 \(j\) 那么包含它的本质不同方案数为 \(g_j=\sum_{k=l}^j f_{i,k}-d_{i,k}\)。
考虑每个位置对连续段 \([l,r]\) 的左端点 \(l\) 的贡献，那么一定是形如下图：
对于非开头的段的贡献是平凡的就是一个简单区间和，对于开头段假设其分界点为 \(l'\) 那么其贡献为 \(g_{l'}+\sum_{k=l'+1}^R f_{i-1,k}\)。
对于非左端点的位置，我们考虑它新加了那些本质不同的方案数，不难发现是 \(f_{i-1,r'_{j}}\)，对于减少了多少方案数那么是 \(d_{i-1,l'_{j}}\)。
但是发现漏情况了，减少的方案数算的不对，因为如果 \(l'_{j-1}\) 与 \(l'_j\) 不属于相同颜色段，那么还要减去一个 \(g_{l'_{j-1}}\)。
T4
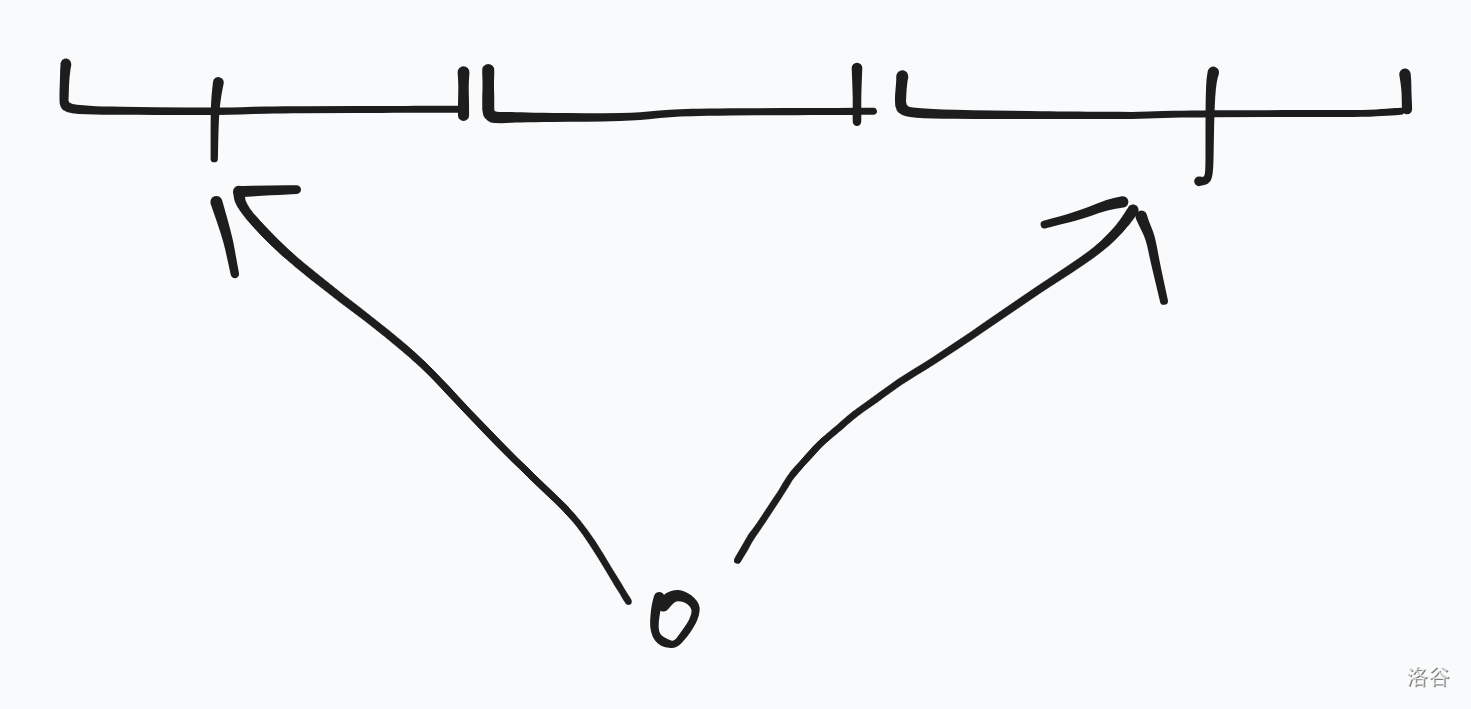
首先对于询问我们可以发现最后的答案一定是形如下图：
并且最大的边一定在左右两侧中的一侧。
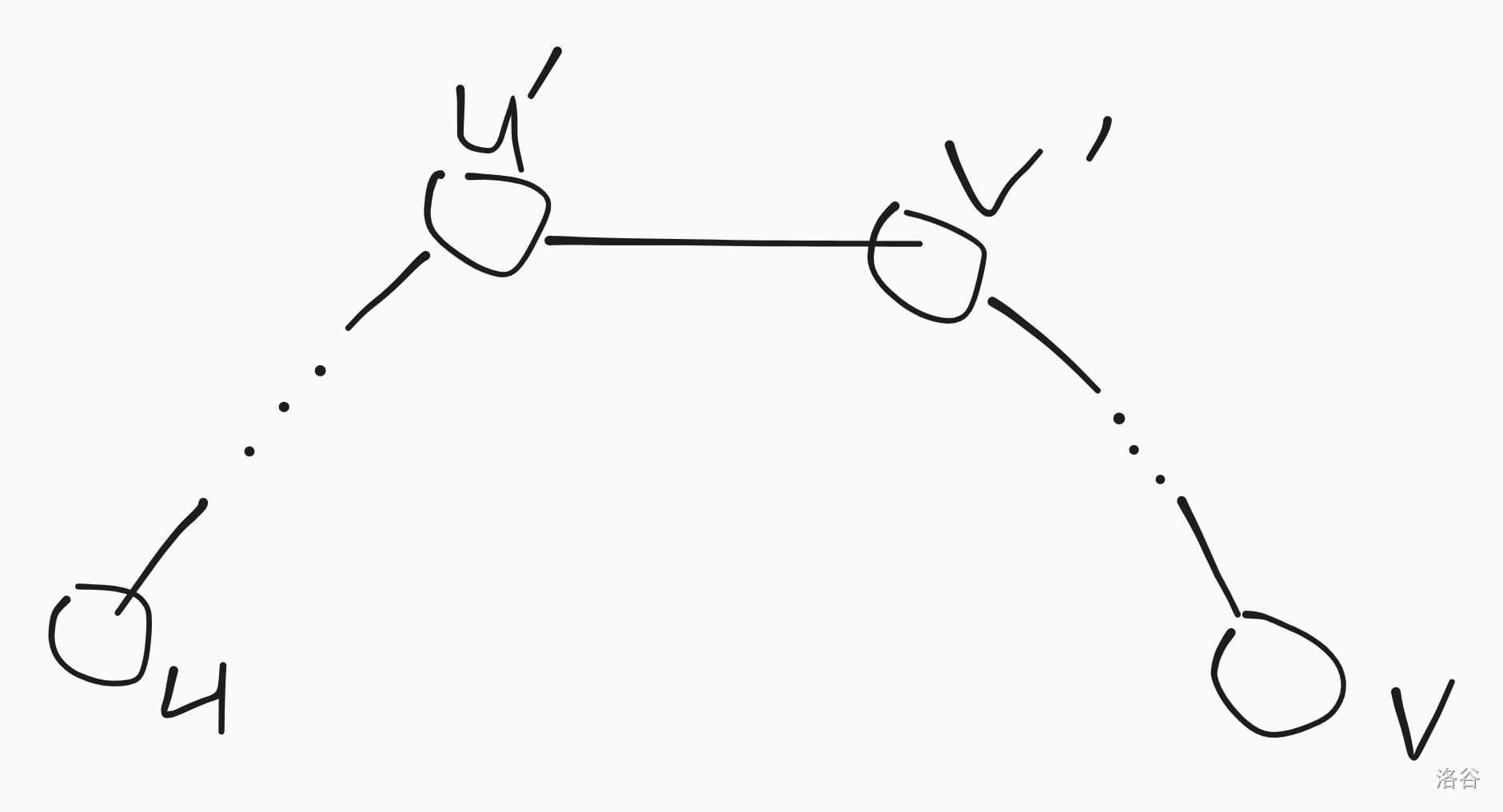
那我们考虑 kruskal 从小到大加边，每次去合并连通块，因为我们是从小到大加的，所以最后答案一定会变成下图：
那么我们考虑合并的时候将出边和询问都合并到一个点上，使用启发式合并可以做到 \(O(n\log^2 n)\)。
11.22
T1
建议改名：【模板】根号分治
T2
你考虑直接上可撤销背包力大砖飞即可，可能需要取个模，但是我选择 __int128。
T3
先离线。
你考虑维护一个长得像历史和的 DS，你维护一个指针 \(r\) 扫一遍整个序列，线段树上每个叶子 \(l\) 代表 \([l,r]\)，这段子区间的前缀中有多少个含有奇数个不同的数。
对于不同的数我们有经典 trick 你记一个 \(pre_i\) 表示与 \(a_{pre_i}=a_i\) 且离 \(i\) 最近的数，那你每次要更改的就是 \([pre_r+1,r]\) 这段区间的奇偶性。
然后你对 \([1,r]\) 这段前缀所有为奇数的点进行一个整体加一，你考虑这个玩意咋维护。
一个比较 navie 的想法是上矩阵，常熟太大，我们有全♂新♂做♂法♂。
考虑维护两棵线段树，然后每次反转奇偶性就是交换对应区间，然后整体加一只对一棵线段树做就行了。
T4
这啥神秘结论题。
先把序列化成 \(0101010101010\dots\) 的形式。
手腕发现结论就是假设序列长 \(m\)，那么答案是去掉首尾排序后前 \(\lfloor\frac{m-1}{2}\rfloor\) 的数的和。
找不到原题也不会证明。
11.27
阿米诺斯，是不是好久没写总结了。
P5350
模拟赛 T4。
之前好像没有做过可持久化平衡树节点太多就暴力重构的题的说。
CF2026F
是没见过的 trick（好吧其实就是 deque 底层逻辑
考虑先把版本树建出来，然后拿两个指针在上面扫，两条指针构成了一条链那么我们实际维护的就是这条链上的背包。
发现如果只有 2 操作是好做的，维护一个栈每个位置存一个 DP 值就行，这样每次 push 一个数是 \(O(m)\) 的，但是加上 3 操作以后，发现不太好修改。
那我们考虑维护两个栈，一个栈存尾指针到分界点的 DP 值，一个栈存分界点到头指针的 DP 值，这个分界点是不定的。
那么 3 操作也能像 2 操作一样实现，但是有个问题就是你某个栈空了该咋整，这里我们考虑把另一个栈的一半栈底倒过去就行。
这个复杂度是均摊 \(O(1)\) 的，这也是 deque 的底层实现。
CF802N
我勒个模拟费用流。
先考虑咋建模，你考虑建出一个 \(s\to u\to t\) 的图，其中中间点集中的点向前一个连无费用边，\(s\to u\) 的费用为 \(b_u\)，\(u\to t\) 的费用为 \(a_u\)。
不难发现这是对的，考虑接下来如何模拟。
有两种做法，先说 WQS 二分加反悔贪心。
反悔贪心是显然的，因为我们使用了 WQS 二分的缘由，我们实际只需关注其代价最小就行。
那么决策有两种：
- 选择之前一个未匹配的 \(a_j\)，若 \(b_i+a_j\le 0\)，就选上并计数器加一；
- 选择之前一个匹配的 \(b_j\)，设其匹配的是 \(a_k\)，若 \(b_i-b_j\le 0\)，就选上。
考虑第二种实际就是把 \(-b_i\) 塞堆里，所以统一维护即可，另外注意能让计数器加一尽量加一。
然后是一个老哥的模拟费用流，懒得实现了，口胡一下。
不难发现我们的一次操作相当于是给 \([j,i]\) 这之间的边流向取反，然后决策是一段前缀匹配一段后缀，或者一段后缀匹配一段前缀的形式，这可以轻易的上线段树维护，就可以做到一个老哥了。
UOJ455
443 downvotes 名不虚传。
首先只对于每个外卖员去考虑餐厅的话不可避免的会带上绝对值非常难以处理，所以我们也让餐厅去考虑外卖员。
这样的话我们让每个点都向左匹配，一个朴素的方法是建四个堆，但是我们考虑合理设置权值使其变为反悔自动机，以下设外卖员的决策时权值为 \(a_i\)，餐厅的决策时权值为 \(b_i\)。
先考虑不反悔的情况，外卖员匹配餐厅代价是 \(a_i-b_j=x_i-(y_j-w_j)\)，餐厅匹配外卖员代价是 \(b_j-a_i=y_j+w_j-x_i\)。
考虑对外卖员反悔，代价为 \(-2a_i+b_j\)，对餐厅反悔代价为 \(-2b_j+a_i\)。
然后把上述代价扔进两个堆然后反悔贪心就行了，注意要对相同权值的合并起来做。
