使用Halcon完成最小二乘法拟合直线

使用Halcon完成最小二乘法拟合直线

本篇博客主要为了展示通过Halcon内的一系列点（不在同一条直线）的集合拟合成一条直线，这里使用的方法为经常用到的最小二乘法，本篇不再对最小二乘的原理进行阐述，而是直接利用其公式\(A^TAX=A^Tb\)，其中A为两列N行的矩阵，其行数等于点的个数，其每行第一个元素为点的X坐标，对应Halcon中的列坐标，而每行的第二个坐标为1，X为一个列向量，第一个元素即为\(y=ax+c\)中的a，而第二个元素为c，b为一列N行的列向量，其每行的元素对应点的Y坐标，即Halcon中的行坐标。

最小二乘法

*****************************最小二乘法拟合直线*****************************

*点数据
Rows := []
Cols := []

*模拟直线数据
a := 1
b := 10
for Index := 0 to 9 by 1
    *y = ax + b
    TempCol := Index * 20
    TempRow := a * TempCol + b
    Rows := [Rows,TempRow]
    Cols := [Cols,TempCol]
endfor

a := 1
b := 20
for Index := 0 to 9 by 1
    *y = ax + b
    TempCol := Index * 20
    TempRow := a * TempCol + b
    Rows := [Rows,TempRow]
    Cols := [Cols,TempCol]
endfor

gen_cross_contour_xld (Cross, Rows, Cols, 6, 0.785398)

*根据最小二乘法公式ATAX = ATb ===> X = (ATA)逆*(ATb)

*创建矩阵A
A := [Cols[0],1,\
      Cols[1],1,\
      Cols[2],1,\
      Cols[3],1,\
      Cols[4],1,\
      Cols[5],1,\
      Cols[6],1,\
      Cols[7],1,\
      Cols[8],1,\
      Cols[9],1,\
      Cols[10],1,\
      Cols[11],1,\
      Cols[12],1,\
      Cols[13],1,\
      Cols[14],1,\
      Cols[15],1,\
      Cols[16],1,\
      Cols[17],1,\
      Cols[18],1,\
      Cols[19],1]
b := [Rows[0],\
      Rows[1],\
      Rows[2],\
      Rows[3],\
      Rows[4],\
      Rows[5],\
      Rows[6],\
      Rows[7],\
      Rows[8],\
      Rows[9],\
      Rows[10],\
      Rows[11],\
      Rows[12],\
      Rows[13],\
      Rows[14],\
      Rows[15],\
      Rows[16],\
      Rows[17],\
      Rows[18],\
      Rows[19]]
      
create_matrix (20, 2,A, MatrixAID)
create_matrix (20, 1,b, MatrixbID)
*计算ATA(其实Halcon里对于AX = b，有直接求解的算子，solve_matrix)
mult_matrix (MatrixAID, MatrixAID, 'ATB', MatrixATAID)
*计算(ATA)逆
invert_matrix (MatrixATAID, 'general', 0, MatrixInvID)
*计算(ATA)逆*AT
mult_matrix (MatrixInvID, MatrixAID, 'ABT', MultMatrixID)
*最终结果
mult_matrix (MultMatrixID, MatrixbID, 'AB', MatrixRes)

get_full_matrix (MatrixRes, Values)
*得到a和b
a := Values[0]
b := Values[1]
*绘制拟合直线
Col1 := 0
Row1 := a * Col1 + b

Col2 := 300
Row2 := a * Col2 + b
gen_contour_polygon_xld (Contour, [Row1,Row2], [Col1,Col2])

---

总共拟合了二十个点，其中十个点来自一条直线，另外十个点来自另外一条直线，则对应于\(A^TX=A^Tb\)中的\(A\)为

\[\left[ \begin{matrix} Col1 & 1 \\ Col2 & 1 \\ Col3 & 1 \\ ... & ... \\ Col20 & 1 \end{matrix} \right] \ \]

而\(b\)则对应

\[\left[ \begin{matrix} Row1\\ Row2\\ Row3\\ ... \\ Row20 \end{matrix} \right] \ \]

---

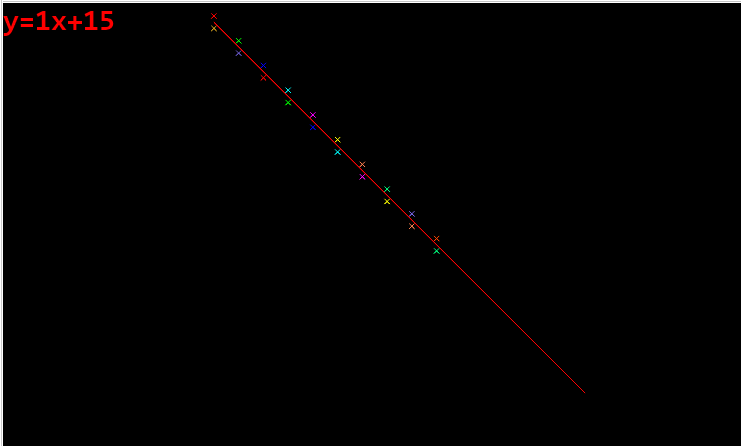
拟合的结果：