BUUCTF [NPUCTF2020]认清形势，建立信心

from Crypto.Util.number import *
from gmpy2 import *
from secret import flag

p = getPrime(25)
e = '# Hidden'
q = getPrime(25)
n = p * q
m = bytes_to_long(flag.strip(b"npuctf{").strip(b"}"))

c = pow(m, e, n)
print(c)
print(pow(2, e, n)) # c1
print(pow(4, e, n)) # c2
print(pow(8, e, n)) # c3

'''
169169912654178

128509160179202
518818742414340
358553002064450
'''

题目告诉了我们三个同余式 我们要想办法求解n和e
这里求n的方法特别经典:构造两个含n的乘积式 通过gcd来求解
推导：

c1^2 = c2 + k2 x n
c1^3 = c3 + k3 x n
=>
k2 x n = c1^2 - c2
k3 x n = c1^3 - c3

这样我们求解gcd然后factor.db分解一下就可以得到n 了
这里gcd=1054494004042394 分解结果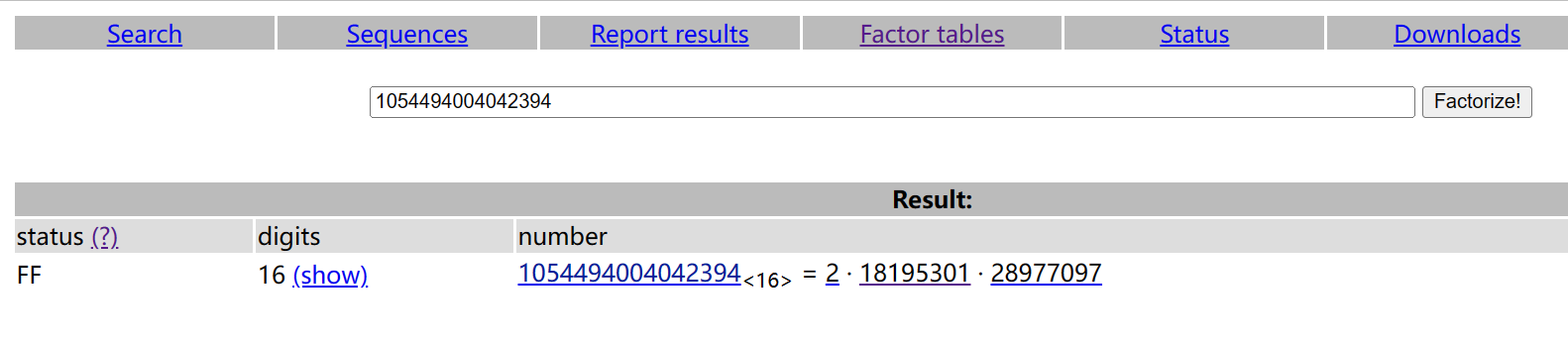
所以去掉2 即为p,q
然后求解e的话直接用sympy自带的discrete_log函数解决即可
exp:

from Crypto.Util.number import *
from gmpy2 import *
from primefac import *
from sympy import *

c1 = 128509160179202
c2 = 518818742414340
c3 = 358553002064450

print(gcd(c1*c1-c2,c1*c1*c1-c3))

p = 18195301
q = 28977097
n = p*q
e = discrete_log(n,c1,2)
print(e)
c = 169169912654178
phi = (p-1)*(q-1)
d = modinv(e,phi)
m = pow(c,d,n)
print(long_to_bytes(m))