P4438
[HNOI/AHOI2018]道路
题目描述
W 国的交通呈一棵树的形状。W 国一共有 \(n-1\) 个城市和 \(n\) 个乡村,其中城市从 \(1\) 到 \(n-1\) 编号,乡村从 \(1\) 到 \(n\) 编号,且 \(1\) 号城市是首都。道路都是单向的,本题中我们只考虑从乡村通往首都的道路网络。
对于每一个城市,恰有一条公路和一条铁路通向这座城市。对于城市 \(i\), 通向该城市的道路(公路或铁路)的起点,要么是一个乡村,要么是一个编号比 \(i\) 大的城市。没有道路通向任何乡村。除了首都以外,从任何城市或乡村出发只有一条道路;首都没有往外的道路。从任何乡村出发,沿着唯一往外的道路走,总可以到达首都。
W 国的国王小 W 获得了一笔资金,他决定用这笔资金来改善交通。由于资金有限,小 W 只能翻修 \(n-1\) 条道路。小 W 决定对每个城市翻修恰好一条通向它的道路,即从公路和铁路中选择一条并进行翻修。小 W 希望从乡村通向城市可以尽可能地便利,于是根据人口调查的数据,小 W 对每个乡村制定了三个参数,编号为 \(i\) 的乡村的三个参数是 \(a_i\),\(b_i\) 和 \(c_i\)。假设从编号为 \(i\) 的乡村走到首都一共需要经过 \(x\) 条未翻修的公路与 \(y\) 条未翻修的铁路,那么该乡村的不便利值为:
在给定的翻修方案下,每个乡村的不便利值相加的和为该翻修方案的不便利值。 翻修 \(n-1\) 条道路有很多方案,其中不便利值最小的方案称为最优翻修方案,小 W 自然希望找到最优翻修方案,请你帮助他求出这个最优翻修方案的不便利值。
输入格式
第一行为正整数 \(n\)。
接下来 \(n - 1\) 行,每行描述一个城市。其中第 \(i\) 行包含两个数 \(s_i,t_i\)。\(s_i\) 表示通向第 \(i\) 座城市的公路的起点,\(t_i\) 表示通向第 \(i\) 座城市的铁路的起点。如果\(s_i>0\),那么存在一条从第 \(s_i\) 座城市通往第\(i\)座城市的公路,否则存在一条从第 \(-s_i\) 个乡村通往第 \(i\) 座城市的公路;\(t_i\) 类似地,如果 \(t_i > 0\),那么存在一条从第 \(t_i\) 座城市通往第 \(i\) 座城市的铁路,否则存在一条从第 \(-t_i\) 个乡村通往第 \(i\) 座城市的铁路。
接下来 \(n\) 行,每行描述一个乡村。其中第 \(i\) 行包含三个数 \(a_i,b_i,c_i\),其意义如题面所示。
输出格式
输出一行一个整数,表示最优翻修方案的不便利值。
样例 #1
样例输入 #1
6
2 3
4 5
-1 -2
-3 -4
-5 -6
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
样例输出 #1
54
样例 #2
样例输入 #2
9
2 -2
3 -3
4 -4
5 -5
6 -6
7 -7
8 -8
-1 -9
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1
样例输出 #2
548
样例 #3
样例输入 #3
12
2 4
5 3
-7 10
11 9
-1 6
8 7
-6 -10
-9 -4
-12 -5
-2 -3
-8 -11
53 26 491
24 58 190
17 37 356
15 51 997
30 19 398
3 45 27
52 55 838
16 18 931
58 24 212
43 25 198
54 15 172
34 5 524
样例输出 #3
5744902
提示
【样例解释 1】
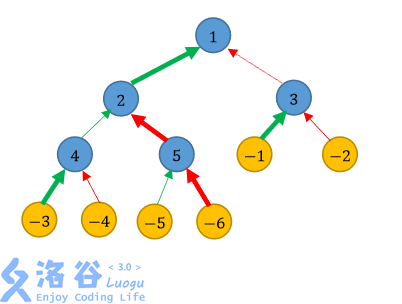
如图所示,我们分别用蓝色、黄色节点表示城市、乡村;用绿色、红色箭头分别表示 公路、铁路;用加粗箭头表示翻修的道路。
一种不便利值等于54的方法是:翻修通往城市2和城市5的铁路,以及通往其他城市的 公路。用→和⇒表示公路和铁路,用∗→和∗⇒表示翻修的公路和铁路,那么:
编号为1的乡村到达首都的路线为:-1 ∗→ 3 ⇒ 1,经过0条未翻修公路和1条未翻修铁 路,代价为3 × (1 + 0) × (2 + 1) = 9;
编号为2的乡村到达首都的路线为:-2 ⇒ 3 ⇒ 1,经过0条未翻修公路和2条未翻修铁 路,代价为2 × (1 + 0) × (3 + 2) = 10;
编号为3的乡村到达首都的路线为:-3 ∗→ 4 → 2 ∗→ 1,经过1条未翻修公路和0条未 翻修铁路,代价为3 × (2 + 1) × (1 + 0) = 9;
编号为4的乡村到达首都的路线为:-4 ⇒ 4 → 2 ∗→ 1,经过1条未翻修公路和1条未翻 修铁路,代价为1 × (2 + 1) × (3 + 1) = 12;
编号为5的乡村到达首都的路线为:-5 → 5 ∗⇒ 2 ∗→ 1,经过1条未翻修公路和0条未 翻修铁路,代价为2 × (3 + 1) × (1 + 0) = 8;
编号为6的乡村到达首都的路线为:-6 ∗⇒ 5 ∗⇒ 2 ∗→ 1,经过0条未翻修公路和0条未翻修铁路,代价为1 × (3 + 0) × (2 + 0) = 6;
总的不便利值为9 + 10 + 9 + 12 + 8 + 6 = 54。可以证明这是本数据的最优解。
【样例解释 2】
在这个样例中,显然应该翻修所有公路。
【数据范围】
一共20组数据,编号为1 ∼ 20。
对于编号\(\le 4\)的数据,\(n \le 20\);
对于编号为5 ∼ 8的数据,\(a_i,b_i,c_i \le 5\),\(n \le 50\);
对于编号为9 ∼ 12的数据,\(n \le 2000\);
对于所有的数据,\(n \le 20000\),\(1 \le a_i,b_i \le 60\),\(1 \le c_i \le 10^9\),\(s_i,t_i\)是\([-n,-1] \cup (i,n - 1]\)内的整数,任意乡村可以通过不超过40条道路到达首都。
自上而下的树形DP
关键在 对于x 和 y 的处理
而且本题只关心叶结点 所以是自上而下的
注意记忆化搜索写的时候边界处理要细致全面!(否则RE || MLE)
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define KASAKI_NOZOMI 伞木希美
const int N=2e4+5;
int inf;
int n,a[N],b[N],c[N],f[N][45][45],ls[N],rs[N];
int dp(int u,int x,int y) { //u--->root : x,y
if(u>=n)//leaf nodes need to be check before dp-ed
return c[u-n+1]*(a[u-n+1]+x)*(b[u-n+1]+y);
if(f[u][x][y]!=inf)return f[u][x][y];//dp-ed
int tmp=inf;
tmp=min(dp(ls[u],x,y)+dp(rs[u],x,y+1),dp(ls[u],x+1,y)+dp(rs[u],x,y));
return f[u][x][y]=tmp;
}
#ifdef KASAKI_NOZOMI
signed main() {
ios::sync_with_stdio(false);
memset(f,0x3f,sizeof(f));
inf=f[0][0][0];
cin>>n;
for(int i=1; i<n; i++) {
int s,t;
cin>>s>>t;
if(s<0)s=-s+n-1;
if(t<0)t=-t+n-1;
ls[i]=s,rs[i]=t;
}
for(int i=1; i<=n; i++)cin>>a[i]>>b[i]>>c[i];
dp(1,0,0);
cout<<f[1][0][0]<<"\n";
return 0;
}
#endif


