P3384 树链剖分实现LCA

[JLOI2009]二叉树问题

题目描述

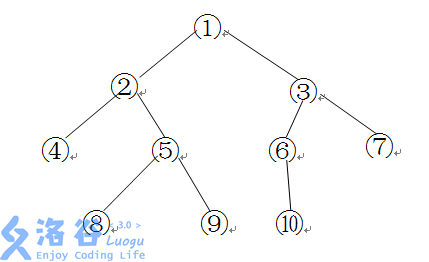
如下图所示的一棵二叉树的深度、宽度及结点间距离分别为：

• 深度：\(4\)
• 宽度：\(4\)
• 结点 8 和 6 之间的距离：\(8\)
• 结点 7 和 6 之间的距离：\(3\)

其中宽度表示二叉树上同一层最多的结点个数，节点 \(u, v\) 之间的距离表示从 \(u\) 到 \(v\) 的最短有向路径上向根节点的边数的两倍加上向叶节点的边数。

给定一颗以 1 号结点为根的二叉树，请求出其深度、宽度和两个指定节点 \(x, y\) 之间的距离。

输入格式

第一行是一个整数，表示树的结点个数 \(n\)。
接下来 \(n - 1\) 行，每行两个整数 \(u, v\)，表示树上存在一条连接 \(u, v\) 的边。
最后一行有两个整数 \(x, y\)，表示求 \(x, y\) 之间的距离。

输出格式

输入三行，每行一个整数，依次表示二叉树的深度、宽度和 \(x, y\) 之间的距离。

样例 #1

样例输入 #1

10                                
1 2                            
1 3                            
2 4
2 5
3 6
3 7
5 8
5 9
6 10
8 6

样例输出 #1

4
4
8

提示

对于全部的测试点，保证 \(1 \leq u, v, x, y \leq n \leq 100\)，且给出的是一棵树。

常规树链剖分操作即可

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e4+5;
int n;
struct Graph{
	int nxt,to;
}edge[N<<1];
int head[N],cnt;
inline void add(int u,int v)
{
	cnt++;
	edge[cnt].to=v;
	edge[cnt].nxt=head[u];
	head[u]=cnt;
}
int dep[N],siz[N],son[N],fa[N],wid[N],maxwid,maxdep;
void dfs1(int u,int fat)
{
	dep[u]=dep[fat]+1,fa[u]=fat,siz[u]=1;wid[dep[u]]++;
	maxwid=max(maxwid,wid[dep[u]]);
	maxdep=max(maxdep,dep[u]);
	int maxson=-1;
	for(int i=head[u];i;i=edge[i].nxt)
	{
		int v=edge[i].to;
		if(v==fat)continue;
		dfs1(v,u);
		siz[u]+=siz[v];
		if(siz[v]>maxson)maxson=siz[v],son[u]=v;
	}
}
int id[N],times=0,top[N];
void dfs2(int u,int topf)
{
	id[u]=++times;
	top[u]=topf;
	if(!son[u])return ;
	dfs2(son[u],topf);
	for(int i=head[u];i;i=edge[i].nxt)
	{
		int v=edge[i].to;
		if(id[v])continue;
		dfs2(v,v);
	}
}
int LCA(int x,int y)
{
	while(top[x]!=top[y])
	{
		if(dep[top[x]]<dep[top[y]])swap(x,y);
		x=fa[top[x]];		
	}
	if(dep[x]>dep[y])swap(x,y);
	return x;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin>>n;
	for(int i=1;i<n;i++)
	{
		int u,v;
		cin>>u>>v;
		add(u,v);
		add(v,u);
	}
	dfs1(1,1);
	dfs2(1,1);
	int x,y;
	cin>>x>>y;cout<<maxdep<<"\n"<<maxwid<<"\n";
	int u=LCA(x,y);
	cout<<2*(dep[x]-dep[u])+(dep[y]-dep[u])<<"\n";
	return 0;
}