P7771 欧拉路径(欧拉回路)

【模板】欧拉路径

题目描述

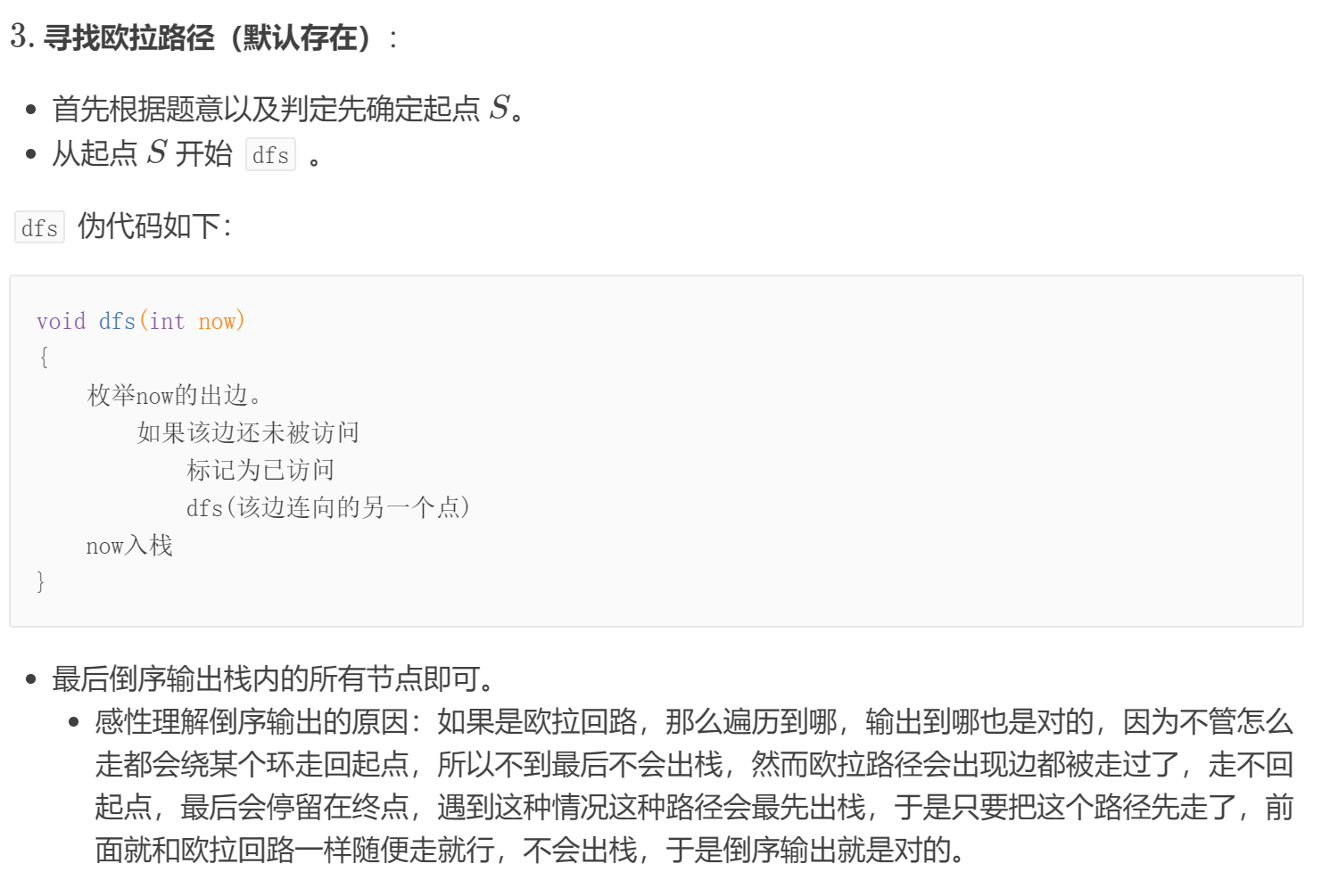
求有向图字典序最小的欧拉路径。

输入格式

第一行两个整数 \(n,m\) 表示有向图的点数和边数。

接下来 \(m\) 行每行两个整数 \(u,v\) 表示存在一条 \(u\to v\) 的有向边。

输出格式

如果不存在欧拉路径，输出一行 No。

否则输出一行 \(m+1\) 个数字，表示字典序最小的欧拉路径。

样例 #1

样例输入 #1

4 6
1 3
2 1
4 2
3 3
1 2
3 4

样例输出 #1

1 2 1 3 3 4 2

样例 #2

样例输入 #2

5 5
1 2
3 5
4 3
3 4
2 3

样例输出 #2

1 2 3 4 3 5

样例 #3

样例输入 #3

4 3
1 2
1 3
1 4

样例输出 #3

No

提示

对于 \(50\%\) 的数据，\(n,m\leq 10^3\)。

对于 \(100\%\) 的数据，\(1\leq u,v\leq n\leq 10^5\)，\(m\leq 2\times 10^5\)。

保证将有向边视为无向边后图连通。

#include<bits/stdc++.h>
// 欧拉路径
// 回路:
// 所有点 in[i]==out[i]
//普通路径:
// 恰有一个点 out[i]==in[i]+1 : START
// 恰有一个点 in[i]==out[i]+1 : END
//字典序最小？
//连边的点要排序 ---> vector --->入栈后 倒序输出
using namespace std;
const int N=2e5+5;
int n,m;
vector<int>G[N];
int stack_[N],pt,in[N],out[N],cnt1,cnt2;
int cur[N];
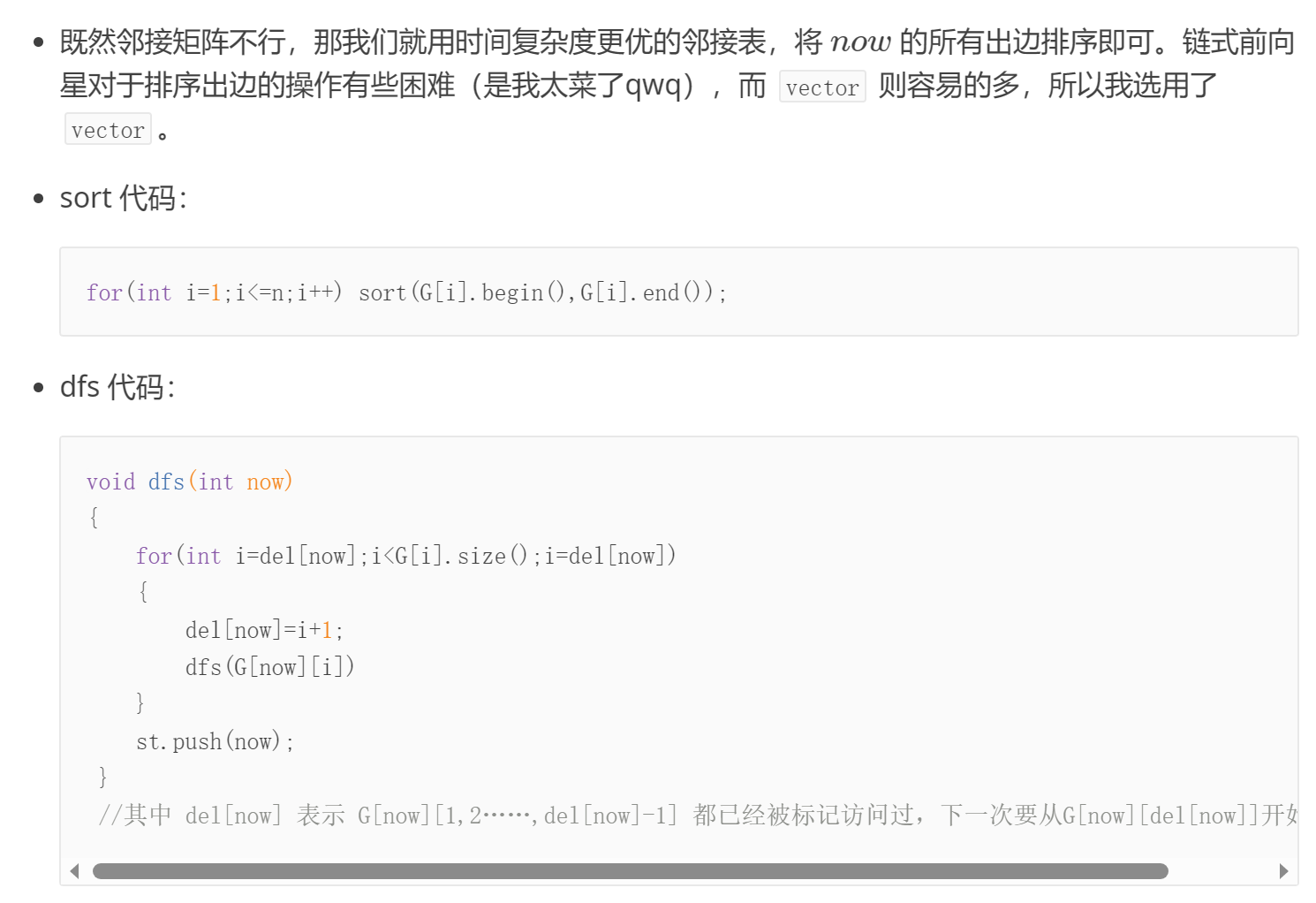
void dfs(int u)
{
	for(int i=cur[u];i<G[u].size();i=cur[u])
	{
		cur[u]=i+1;
		dfs(G[u][i]);
	}
	stack_[++pt]=u;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		int u,v;
		cin>>u>>v;
		G[u].push_back(v);
		out[u]++,in[v]++;
	}
	for(int i=1;i<=n;i++)
		sort(G[i].begin(),G[i].end());
	int is_loop=1;//判断欧拉回路 
	int Start=1;//！！！！！ 
	for(int i=1;i<=n;i++)
	{
		if(in[i]!=out[i])
		{
			is_loop=0;
			if(out[i]==in[i]+1)
			{
				Start=i;
				cnt1++;
			}
			else if(in[i]==out[i]+1){
				cnt2++;
			}
			else{
				cout<<"No\n";
				return 0;
			}
		}
	}
	if(is_loop=0&&!(cnt1==1&&cnt2==1)){
		cout<<"No\n";
		return 0;
	}
	dfs(Start);
	while(pt>0)
	{
		cout<<stack_[pt]<<" ";
		pt--;
	}
	return 0;
}