P5960 差分约束系统

【模板】差分约束算法

题目描述

给出一组包含 \(m\) 个不等式，有 \(n\) 个未知数的形如：

\[\begin{cases} x_{c_1}-x_{c'_1}\leq y_1 \\x_{c_2}-x_{c'_2} \leq y_2 \\ \cdots\\ x_{c_m} - x_{c'_m}\leq y_m\end{cases} \]

的不等式组，求任意一组满足这个不等式组的解。

输入格式

第一行为两个正整数 \(n,m\)，代表未知数的数量和不等式的数量。

接下来 \(m\) 行，每行包含三个整数 \(c,c',y\)，代表一个不等式 \(x_c-x_{c'}\leq y\)。

输出格式

一行，\(n\) 个数，表示 \(x_1 , x_2 \cdots x_n\) 的一组可行解，如果有多组解，请输出任意一组，无解请输出 NO。

样例 #1

样例输入 #1

3 3
1 2 3
2 3 -2
1 3 1

样例输出 #1

5 3 5

提示

样例解释

\(\begin{cases}x_1-x_2\leq 3 \\ x_2 - x_3 \leq -2 \\ x_1 - x_3 \leq 1 \end{cases}\)

一种可行的方法是 \(x_1 = 5, x_2 = 3, x_3 = 5\)。

\(\begin{cases}5-3 = 2\leq 3 \\ 3 - 5 = -2 \leq -2 \\ 5 - 5 = 0\leq 1 \end{cases}\)

数据范围

对于 \(100\%\) 的数据，\(1\leq n,m \leq 5\times 10^3\)，\(-10^4\leq y\leq 10^4\)，\(1\leq c,c'\leq n\)，\(c \neq c'\)。

原理：

注意 我们要建立一个超级源点 保证所有点联通

连边方法

注意两种建边方式跑出来结果的区别

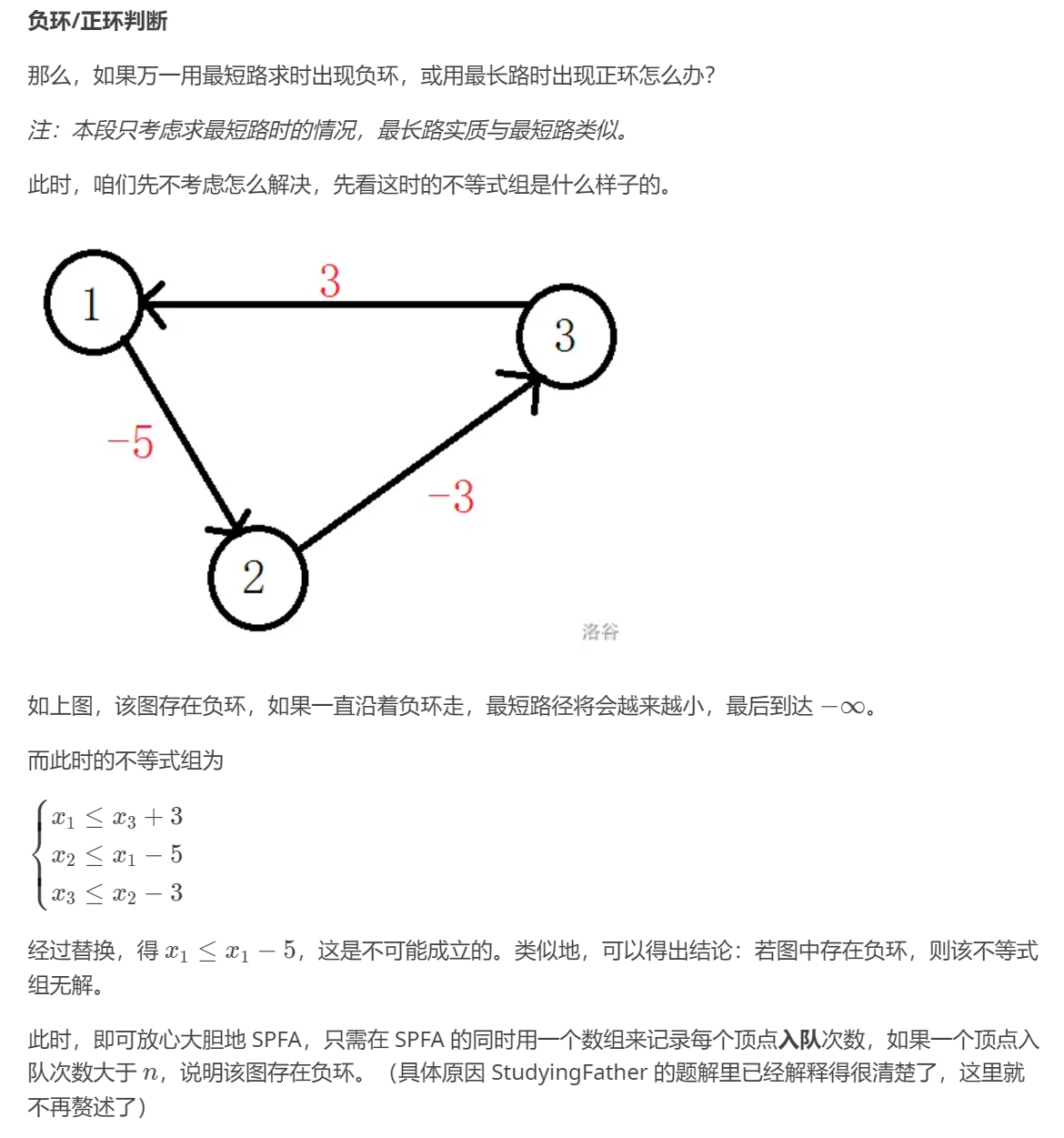
负环

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=5e3+5;
int n,m;
struct Graph{
	int nxt,to,val;
}edge[N<<1];
int head[N],cnt,in[N];
inline void add(int u,int v,int w)
{
	cnt++;
	edge[cnt].to=v;
	edge[cnt].val=w;
	edge[cnt].nxt=head[u];
	head[u]=cnt;
}
int vis[N],dis[N];
bool spfa(int s)
{
	queue<int>q;
	q.push(s);
	vis[s]=1;
	memset(dis,0x3f,sizeof(dis));
	dis[s]=0;
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		vis[u]=0;
		for(int i=head[u];i;i=edge[i].nxt)
		{
			int v=edge[i].to;
			int w=edge[i].val;
			if(dis[u]+w<dis[v])
			{
				dis[v]=dis[u]+w;
				if(!vis[v])
				{
					vis[v]=1;
					q.push(v);
					in[v]++;
					if(in[v]>n+1)return false;//注意 有 n+1个点(包括超级源点) 
				}
			}
		}
	}
}
signed main()
{
	ios::sync_with_stdio(false);
	cin>>n>>m;
	for(int i=1;i<=n;i++)add(0,i,0);// 建立0点 为超级源点 
	
	for(int i=1;i<=m;i++)
	{
		int x,y,w;
		cin>>x>>y>>w;
		add(y,x,w);
	}
	int pd=spfa(0);
	if(!pd)// 有负环  即无解
		cout<<"NO\n";
	else
	{
		for(int i=1;i<=n;i++)
			cout<<dis[i]<<" ";
		cout<<"\n";
	}
	return 0;
}