P8785

[蓝桥杯 2022 省 B] 扫雷

题目描述

小明最近迷上了一款名为《扫雷》的游戏。其中有一个关卡的任务如下，在一个二维平面上放置着 \(n\) 个炸雷，第 \(i\) 个炸雷 \(\left(x_{i}, y_{i}, r_{i}\right)\) 表示在坐标 \(\left(x_{i}, y_{i}\right)\) 处存在一个炸雷，它的爆炸范围是以半径为 \(r_{i}\) 的一个圆。

为了顺利通过这片土地，需要玩家进行排雷。玩家可以发射 \(m\) 个排雷火箭，小明已经规划好了每个排雷火箭的发射方向，第 \(j\) 个排雷火箭 \(\left(x_{j}, y_{j}, r_{j}\right)\) 表示这个排雷火箭将会在 \(\left(x_{j}, y_{j}\right)\) 处爆炸，它的爆炸范围是以半径为 \(r_{j}\) 的一个圆，在其爆炸范围内的炸雷会被引爆。同时，当炸雷被引爆时，在其爆炸范围内的炸雷也会被引爆。现在小明想知道他这次共引爆了几颗炸雷?

你可以把炸雷和排雷火箭都视为平面上的一个点。一个点处可以存在多个炸雷和排雷火箭。当炸雷位于爆炸范围的边界上时也会被引爆。

输入格式

输入的第一行包含两个整数 \(n\)、\(m\)。

接下来的 \(n\) 行, 每行三个整数 \(x_{i}, y_{i}, r_{i}\), 表示一个炸雷的信息。

再接下来的 \(m\) 行，每行三个整数 \(x_{j}, y_{j}, r_{j}\), 表示一个排雷火箭的信息。

输出格式

输出一个整数表示答案。

样例 #1

样例输入 #1

2 1
2 2 4
4 4 2
0 0 5

样例输出 #1

2

提示

【样例说明】

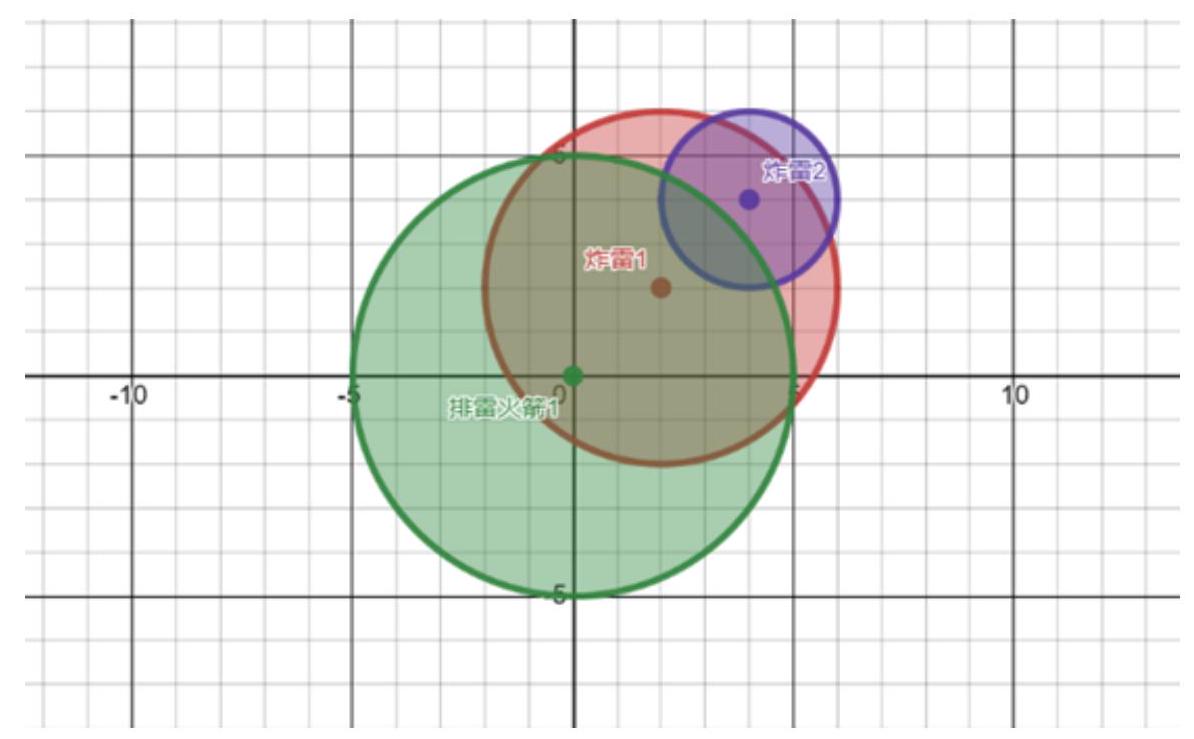
示例图如下, 排雷火箭 1 覆盖了炸雷 1 , 所以炸雷 1 被排除; 炸雷 1 又覆 盖了炸雷 2 , 所以炸雷 2 也被排除。

【评测用例规模与约定】

对于 \(40 \%\) 的评测用例: \(0 \leq x, y \leq 10^{9}, 0 \leq n, m \leq 10^{3}, 1 \leq r \leq 10\).

对于 \(100 \%\) 的评测用例: \(0 \leq x, y \leq 10^{9}, 0 \leq n, m \leq 5 \times 10^{4}, 1 \leq r \leq 10\).

首先很显然是一道 dfs 题 因为每次爆了过后会引发新的爆炸

注意到 r<=10 而 x y 很大

很显然 对于 a[i] a[j] 若 |a[i].x-a[j].x|>r 那么直接pass

因此我们将n个雷按 x 递增排序

则只需要每次发射炸雷时 二分查找 b[i].x-b[i].r~b[i].x+b[i].r的部分的a[]即可 对于递归的依然如此寻找

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=5e4+5;
struct dd{
	int x,y,r;
	int flag=0;
}a[N];//n
struct did{
	int x,y,r;
}b[N];//m
int cmp(dd c,dd d){return c.x<d.x;}
int n,m;
int ans=0;
double dis(int sx,int sy,int tx,int ty)
{
	return (double)sqrt(((sx-tx)*(sx-tx)+(sy-ty)*(sy-ty)));
}
void dfs(int x,int y,int r)
{
	int lpos,rpos;
	int L=1,R=n,mid;
	while(L<=R)
	{
		mid=(L+R)>>1;
		if(a[mid].x<x-r)L=mid+1;
		else R=mid-1;
	}
	lpos=L;
	L=1,R=n;
	while(L<=R)
	{
		mid=(L+R)>>1;
		if(a[mid].x>x+r)R=mid-1;
		else L=mid+1;
	}
	rpos=R;
	for(int i=lpos;i<=rpos;i++)
	{
		if(!a[i].flag&&dis(a[i].x,a[i].y,x,y)<=r)
		{
			ans++;
			a[i].flag=1;
			dfs(a[i].x,a[i].y,a[i].r);	
		}
	}
}
signed main()
{
	ios::sync_with_stdio(false);
	cin>>n>>m;
	for(int i=1;i<=n;i++)cin>>a[i].x>>a[i].y>>a[i].r;
	//if we have |a[i].x-b[j].x|>r we can pass
	for(int i=1;i<=m;i++)cin>>b[i].x>>b[i].y>>b[i].r;
	// for each b[i] we just need to dfs b[i].x-r~b[i].x+r
	// so does a[i] a[j] …
	sort(a+1,a+n+1,cmp);
	for(int i=1;i<=m;i++)
	{
		if(ans==n)break;
		dfs(b[i].x,b[i].y,b[i].r);
	}
	cout<<ans<<"\n";
	return 0;
}