lqb OI | Practice Plan

整体训练思路:

以luogu的题为主
搜索是重点 然后是数据结构部分 把网络流之前的板子背下来 dp推不来算求了...

搜索
图论
STL
贪心/分治
DP
线段树/平衡树(pbds)

目录

• 整体训练思路:
• 搜索
  • P1189 SEARCH
  • P1278 单词游戏
  • P1406 方格填数
  • P1434 [SHOI2002] 滑雪
  • P1585 魔法阵
  • P1032 字串变换
• STL/数据结构
  • P5250 【深基17.例5】木材仓库
  • P1503 鬼子进村
  • P3369 【模板】普通平衡树
  • 线段树
  • 树状数组
  • 堆
  • 单调队列
  • 单调栈
• 图论
  • 最短路
    • 堆优化Dijkstra
    • SPFA
    • Floyd
  • MST
  • 拓扑排序
  • 欧拉路径(回路)
    • 有向图
    • 无向图
  • 差分约束系统
    • 最短路版:
    • 最长路版
  • 无向图的最小环
  • 二分图匹配-匈牙利算法
• 树
  • 树形DP
    • 换根DP
  • LCA
  • 树上差分
    • 点差分
    • 边差分
  • 树的直径
• 字符串
  • 字典树
  • KMP
• DP/贪心/分治
• 数论
  • 线性筛素数
  • 扩展欧几里得算法
  • 卢卡斯定理
• 其它
  • 高精度
    • Hanoi双塔
    • 最大乘积

搜索

P1189 SEARCH

有意思的一个记忆化搜索 注意到经常会走到同样的状态
(x,y) and face z
数据范围很小 可以开数组存状态 vis[x][y][z]
然后就写一个基本的dfs 注意下边界条件 以及return的点
exp:

#include<bits/stdc++.h>
using namespace std;
int R,C,n;
char a[55][55];string fx[1005];
int vis[55][55][1005]; // record (x,y) and fx[z]
int sx,sy; // start point
char ans[55][55];
#define ISDEBUG 0
void dfs(int x,int y,int z){
	if(a[x][y]=='X')return ;
	if(x<0||y<0||x>R||y>C)return ;
	if(vis[x][y][z]) return;
	if(z==n+1){
		ans[x][y]='*';
		return ;
	}
	if(ISDEBUG){
		cout<<"("<<x<<","<<y<<") "<<z<<"\n";
	}
	int l=0;
	vis[x][y][z]=1;
	if(fx[z]=="NORTH"){
		for(int i=x-1;i>=1;i--){
			if(a[i][y]=='X')break;
			dfs(i,y,z+1);
		}
		
	}
	if(fx[z]=="SOUTH"){
		for(int i=x+1;i<=R;i++){
			if(a[i][y]=='X')break;
			dfs(i,y,z+1);
		}
	}
	if(fx[z]=="WEST"){
		for(int i=y-1;i>=1;i--){
			if(a[x][i]=='X')break;
			dfs(x,i,z+1);
		}
	}
	if(fx[z]=="EAST"){
		for(int i=y+1;i<=C;i++){
			if(a[x][i]=='X')break;
			dfs(x,i,z+1);
		}
	}
	
}
signed main(){
	ios::sync_with_stdio(false);
	cin>>R>>C;
	for(int i=1;i<=R;i++)
		for(int j=1;j<=C;j++){
			cin>>a[i][j];
			ans[i][j]=a[i][j];
			if(a[i][j]=='*')
				sx=i,sy=j,ans[i][j]='.',a[i][j]='.';
			
		}
	cin>>n;
	for(int i=1;i<=n;i++)cin>>fx[i];
	dfs(sx,sy,1);
	for(int i=1;i<=R;i++){
		for(int j=1;j<=C;j++)
			cout<<ans[i][j];
		cout<<"\n";
	}
	return 0;
}

P1278 单词游戏

最暴力的剪枝233
超过时限次数就直接output...

#include<bits/stdc++.h>
using namespace std;
string a[17];
int n;int vis[17];int l[17];
int _time=0;
int maxx=-1;
#define CHEAT 1
void dfs(char ed,int len){
	if(CHEAT){
		_time++;
		if(_time>1e7){
			cout<<maxx<<"\n";
			exit(0);
		}
	}
	maxx=max(maxx,len);
	for(int i=1;i<=n;i++){
		if((!vis[i])&&(a[i][0]==ed)){
			vis[i]=1;
			dfs(a[i][l[i]-1],len+l[i]);
			vis[i]=0;
		}
	}
	
}
signed main(){
	ios::sync_with_stdio(false);
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		l[i]=a[i].length();
	}
	for(int i=1;i<=n;i++){
		vis[i]=1;
		dfs(a[i][l[i]-1],l[i]);
		vis[i]=0;
	}
	cout<<maxx<<"\n";
	return 0;
}

P1406 方格填数

n=4的时候加一些可行性剪枝 比如x==n和y==n可以剪一剪 对角线可以剪一剪
exp:

#include<bits/stdc++.h>
using namespace std;
#define DEBUG 0
int n,a[17],tot=0,s,vis[17],ans[5][5];
int check(int x,int y){
	if(y==n){
		for(int i=1;i<=x;i++){
			int sum=0;
			for(int j=1;j<=n;j++)sum+=ans[i][j];
			if(sum!=s)return 0;
		}
	}
	if(x==n){
		for(int i=1;i<=y;i++){
			int sum=0;
			for(int j=1;j<=n;j++)sum+=ans[j][i];
			if(sum!=s)return 0;
		}
	}
	if(y==n){
		if(x>=1){
			int sum=0;
			for(int i=1;i<=n;i++)sum+=ans[i][n+1-i];
			if(sum!=s)return 0;
		}
		if(x==n){
			int sum=0;
			for(int i=1;i<=n;i++)sum+=ans[i][i];
			if(sum!=s)return 0;
		}
	}
	return 1;
}
int check2(int x,int y){
	if(y==n){
		for(int i=1;i<=x-1;i++){
			int sum=0;
			for(int j=1;j<=n;j++)sum+=ans[i][j];
			if(sum!=s)return 0;
		}
	}
	if(x==n){
		for(int i=1;i<=y-1;i++){
			int sum=0;
			for(int j=1;j<=n;j++)sum+=ans[j][i];
			if(sum!=s)return 0;
		}
	}
	if(x==n&&y>1){
		int sum=0;
		for(int i=1;i<=n;i++)sum+=ans[i][n+1-i];
		if(sum!=s)return 0;
	}
	return 1;
}
void dfs(int x,int y){
	if(DEBUG){
		cout<<x<<"   "<<y<<"\n";
	}
	if(!check2(x,y))return ;
	if(x==n+1&&y==1){
		if(!check(n,n)){
			return ;
		}
		cout<<s<<"\n";
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++)
				cout<<ans[i][j]<<" ";
			cout<<"\n";
		}
		exit(0);
	}
	for(int i=1;i<=n*n;i++){
		if(!vis[i]){
			vis[i]=1;
			ans[x][y]=a[i];
			if(1){
			
			if(y==n)dfs(x+1,1);
			else dfs(x,y+1);
		}
			ans[x][y]=0;
			vis[i]=0;
		}
	}
}
int cmp(int x,int y){
	return x<y;
}
signed main(){
	ios::sync_with_stdio(false);
	cin>>n;
	for(int i=1;i<=n*n;i++){
		cin>>a[i];
		tot+=a[i];
	}
	s=tot/n;
	sort(a+1,a+n*n+1,cmp);
	dfs(1,1);
	return 0;
}

P1434 [SHOI2002] 滑雪

经典的记忆化搜索了 开个f[x][y]记录一下 dp用dfs写更加自然 边界也更好判定
exp:

#include<bits/stdc++.h>
using namespace std;
int r,c,a[105][105],f[105][105];
int dx[4]={1,0,-1,0};
int dy[4]={0,1,0,-1};
int dfs(int x,int y){
	if(f[x][y])return f[x][y];
	
	int tmp=0;
	for(int i=0;i<4;i++){
		int nx,ny;
		nx=x+dx[i],ny=y+dy[i];
		if(nx<1||ny<1||nx>r||ny>c)continue;
		if(a[nx][ny]<a[x][y])
			tmp=max(tmp,dfs(nx,ny));
	}
	return f[x][y]=tmp+1;
}
signed main(){
	ios::sync_with_stdio(false);
	cin>>r>>c;
	for(int i=1;i<=r;i++)
		for(int j=1;j<=c;j++)
			cin>>a[i][j];
	int maxx=-1;
	for(int i=1;i<=r;i++)
		for(int j=1;j<=c;j++)
			maxx=max(maxx,dfs(i,j));
	cout<<maxx<<"\n";
	return 0;
}

P1585 魔法阵

80pts版本

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m,k1,k2,MOD;
int minn=INT_MAX;
bool vis[55][55];
int jl[1300][2];
int dx[4]={0,1,0,-1};
int dy[4]={1,0,-1,0};
void dfs(int x,int y,int cnt,int maxx){
	if(cnt==n*m){
		int id = (cnt)%MOD;
		int val = k1*abs(x-jl[id][0])+k2*abs(y-jl[id][1]);
		minn = min(minn,max(maxx,val));
		return ;
	}
	if(maxx>=minn)return ;
	for(int i=0;i<4;i++){
		int nx = x+dx[i];
		int ny = y+dy[i];
		if(nx<1||ny<1||nx>n||ny>m||vis[nx][ny])continue;
		int id = (cnt)%MOD;
		int now_maxx = maxx;
		if(jl[id][0]!=0){
			int val = k1*abs(x-jl[id][0])+k2*abs(y-jl[id][1]);
			now_maxx = max(maxx,val);
			vis[nx][ny] = 1;
			dfs(nx,ny,cnt+1,now_maxx);
			vis[nx][ny] = 0;
		}
		else{
			jl[id][0] = x, jl[id][1] = y;
			vis[nx][ny] = 1;
			dfs(nx,ny,cnt+1,maxx);
			jl[id][0] = 0, jl[id][1] = 0;
			vis[nx][ny] = 0;
		}
	}
	
}
signed main(){
	ios::sync_with_stdio(false);
	cin>>n>>m>>k1>>k2;
	MOD = n*m/2;
	jl[1][0] = 1, jl[1][1] = 1;
	vis[1][1] = 1;
	dfs(1,1,1,0);
	cout<<minn<<"\n";
	return 0;
}

这题可以做一个可行性剪枝 因为很多走法是无法遍历所有格点的
比如当前点为 (x,y)
我发现 我的左右都走过了(或者是边界) 而上下都没走过 那么肯定是不行的
同理 我的上下都走过了(或者是边界) 而左右都没走过 那么也是不行的

exp:

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m,k1,k2,MOD;
int minn=INT_MAX;
bool vis[55][55];
int jl[1300][2];
int dx[4]={0,1,0,-1};
int dy[4]={1,0,-1,0};
void dfs(int x,int y,int cnt,int maxx){
	if(cnt==n*m){
		int id = (cnt)%MOD;
		int val = k1*abs(x-jl[id][0])+k2*abs(y-jl[id][1]);
		minn = min(minn,max(maxx,val));
		return ;
	}
	if(maxx>=minn)return ;
	// to-cut
	if(vis[x-1][y]&vis[x+1][y]&!vis[x][y-1]&!vis[x][y+1])return ;
	if(!vis[x-1][y]&!vis[x+1][y]&vis[x][y-1]&vis[x][y+1])return ;	
	//
	for(int i=0;i<4;i++){
		int nx = x+dx[i];
		int ny = y+dy[i];
		if(nx<1||ny<1||nx>n||ny>m||vis[nx][ny])continue;
		int id = (cnt)%MOD;
		int now_maxx = maxx;
		if(jl[id][0]!=0){
			int val = k1*abs(x-jl[id][0])+k2*abs(y-jl[id][1]);
			now_maxx = max(maxx,val);
			vis[nx][ny] = 1;
			dfs(nx,ny,cnt+1,now_maxx);
			vis[nx][ny] = 0;
		}
		else{
			jl[id][0] = x, jl[id][1] = y;
			vis[nx][ny] = 1;
			dfs(nx,ny,cnt+1,maxx);
			jl[id][0] = 0, jl[id][1] = 0;
			vis[nx][ny] = 0;
		}
	}
	
}
signed main(){
	ios::sync_with_stdio(false);
	cin>>n>>m>>k1>>k2;
	for(int i=0;i<=n+1;i++)
		vis[i][0] = vis[i][m+1] = 1;
	for(int j=0;j<=m+1;j++)
		vis[0][j] = vis[n+1][j] = 1;
	MOD = n*m/2;
	jl[1][0] = 1, jl[1][1] = 1;
	vis[1][1] = 1;
	dfs(1,1,1,0);
	cout<<minn<<"\n";
	return 0;
}

Accepted

P1032 字串变换

bfs 回忆了一下 queue 和 set的一些用法 还有 s.find() string::npos 等 抽时间把STL专练一下

80pts'exp:

#include<bits/stdc++.h>
using namespace std;
#define int long long
string A,B;
string s1[1005],s2[1005];int n;
struct did{
	int c;
	string now;
};
set<string>st;
int flag=0;
void bfs(){
	queue<did>q;
	did z;
	z.c = 0;z.now = A;
	q.push(z);st.insert(A);
	while(!q.empty()){
		z = q.front();
		q.pop();
		string s = z.now;
		if(z.c>10){
			cout<<"NO ANSWER!\n";
			flag = 1;
			return ;
		}
		if(s == B){
			flag = 1;
			cout<<z.c<<"\n";
			return ;
		}
		string t;
		int l1 = s.length();
		for(int i=1;i<=n;i++){
			t = "";
			auto it = s.find(s1[i]);
			if(it!=string::npos){
				int l2 = s1[i].length(),l3 = s2[i].length();
				for(int k=0;k<it;k++)t += s[k];
				t += s2[i];
				for(int k=it+l2;k<l1;k++)t += s[k];
				if(!st.count(t)){
					st.insert(t);
					did d;
					d.c = z.c+1;
					d.now = t;
					q.push(d);
				}
			}
		}
	}
}
signed main(){
	ios::sync_with_stdio(false);
	cin>>A>>B;
	string s,t;
	while(cin>>s>>t){
		n++;
		s1[n] = s,s2[n] = t;
	}
	bfs();
	if(!flag){
		cout<<"NO ANSWER!\n";
	}
	return 0;
}

懒得管了...

STL/数据结构

C++的强大特性 骗分利器!

P5250 【深基17.例5】木材仓库

用map实现
要注意STL的end都是空迭代器！！ 而不是最后一个元素！！！

#include<bits/stdc++.h>
using namespace std;
#define int long long
map<int,int>mp;
signed main(){
	ios::sync_with_stdio(false);
	int n;
	cin>>n;
	while(n--){
		int a,b;
		cin>>a>>b;
		if(a==1){
			if(mp.count(b))cout<<"Already Exist\n";
			else mp[b]=1;
		}
		if(a==2){
			if(mp.size()==0)cout<<"Empty\n";
			else if(mp.count(b)){
				mp.erase(b);
				cout<<b<<"\n";
			}
			else{
				mp[b] = 1;
				auto it = mp.find(b);
				auto it3=it;
				auto it2 = it;
				it++;
				if(it == mp.end()){
					cout<<(--it2)->first<<"\n";
					mp.erase(it2);
				}
				else if(it2 == mp.begin()){
					cout<<(it)->first<<"\n";
					mp.erase(it);
				}
				else if(b-(--it2)->first>(it)->first-b){
					cout<<(it)->first<<"\n";
					mp.erase(it);
				}
				else{
					cout<<(it2)->first<<"\n";
					mp.erase(it2);
				}
				mp.erase(it3);
			}
		}
	}
}

P1503 鬼子进村

一道典型的需要 插入 删除 查找前驱后驱的数据结构题
用pbds来实现平衡树
好久没打了 跟着敲一遍

exp:

#include<bits/stdc++.h>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/tree_policy.hpp>
using namespace std;
using namespace __gnu_cxx;
using namespace __gnu_pbds;
#define int long long
typedef tree<int,null_type,less<int>,rb_tree_tag,tree_order_statistics_node_update>Tree;
const int N=5e4+5;
int n,m;
int _stack[N],pt,vis[N];
Tree tr;
signed main(){
	ios::sync_with_stdio(false);
	cin>>n>>m;
	tr.insert(0);
	tr.insert(n+1);
	for(int i=1;i<=m;i++){
		char op;
		int x;
		cin>>op;
		if(op=='D'){
			cin>>x;
			_stack[++pt] = x;
			vis[x] = 1;
			tr.insert(x);
		}
		if(op=='R'){	
			x = _stack[pt];
			tr.erase(x);
			vis[x] = 0;
			pt--;
		}
		if(op=='Q'){
			cin>>x;
			if(vis[x])cout<<"0\n";
			else{
				auto it1 = tr.lower_bound(x); // >=
				auto it2 = tr.upper_bound(x); // >
				it1--; // <
				int a = *it1,b = *it2;
				cout<<b-a-1<<"\n";
				
			}
		}
	}
	return 0;
}

这里体现了用STL做题一个很重要的步骤 开局设置起始值和结束值！！！
pbds的板子要背一背 头文件和命名空间都要背住

P3369 【模板】普通平衡树

用pbds+pair时间戳 实现

#include<bits/stdc++.h>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/tree_policy.hpp>
using namespace std;
using namespace __gnu_cxx;
using namespace __gnu_pbds;
typedef pair<int,int> pii;
#define int long long
#define mp make_pair
typedef tree<pii,null_type,less<pii>,rb_tree_tag,tree_order_statistics_node_update> Tree;
Tree tr;
int times,n;
void read(int &x){
	x = 0;
	int f = 1;
	char ch = getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-')f=-1;
		ch = getchar();
	}
	while(ch>='0'&&ch<='9'){
		x = 10*x+ch-48;
		ch = getchar();
	}
	x = x*f;
}
void write(int x){
	if(x<0)putchar('-'),x = -x;
	if(x>9)write(x/10);
	putchar(x%10+'0');
}
signed main(){
	read(n);
	for(int i=1;i<=n;i++){
		int op,x;
		read(op),read(x);
		if(op==1){
			times++;
			tr.insert(mp(x,times));
		}
		if(op==2){
			auto it = tr.lower_bound(mp(x,0));
			tr.erase(it);
		}
		if(op==3){
			int rk = tr.order_of_key(mp(x,0))+1;
			write(rk);
			putchar('\n');
		}
		if(op==4){
			auto it = tr.find_by_order(x-1);
			int val = it->first;
			write(val);
			putchar('\n');
		}
		if(op==5){
			auto it = tr.lower_bound(mp(x,0));
			it--;
			int val = it->first;
			write(val);
			putchar('\n');
		}
		if(op==6){
			auto it = tr.upper_bound(mp(x,n+1));
			int val = it->first;
			write(val);
			putchar('\n');
		}
	}
	return 0;
}

背板子注意细节！！！

// insert
times++;
tr.insert(mp(x,times));

// delete only one
auto it = tr.lower_bound(mp(x,0));
tr.erase(it);

// find kth
auto it = tr.find_by_order(k-1);
int val = it->first;

// the order of x
int rk = tr.order_of_key(x)+1; //0->1 so we +1

// find pre
auto it = tr.lower_bound(mp(x,0));
it--;
int val = it->first;

// find after
auto it = tr.upper_bound(mp(x,n+1));
int val = it->first;

线段树

直接打线段树2的板子
注意细节！！！ 先乘后加 mul始终不能为0 更新完懒标记后要
tr[p].add = 0 tr[p].mul = 1 !!!
建树build的时候 mid取的是 (l+r)>>1 !!!
而且query和modify都要记得pushdown!!!

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e5+5;
int n,m,mod,a[N];
struct SegTree{
	int l,r,sum,add,mul;
}tr[N<<2];
void MOD(int &x){
	x = (x%mod+mod)%mod;
}
void pushup(int p){
	tr[p].sum = tr[p<<1].sum + tr[p<<1|1].sum;
	MOD(tr[p].sum);
}
void pushdown(int p){
	tr[p<<1].sum = tr[p].mul*tr[p<<1].sum + tr[p].add*(tr[p<<1].r-tr[p<<1].l+1);
	MOD(tr[p<<1].sum);
	tr[p<<1|1].sum = tr[p].mul*tr[p<<1|1].sum + tr[p].add*(tr[p<<1|1].r-tr[p<<1|1].l+1);
	MOD(tr[p<<1|1].sum);
	tr[p<<1].add = tr[p].mul*tr[p<<1].add + tr[p].add;
	MOD(tr[p<<1].add);
	tr[p<<1|1].add = tr[p].mul*tr[p<<1|1].add + tr[p].add;
	MOD(tr[p<<1|1].add);
	tr[p<<1].mul = tr[p].mul*tr[p<<1].mul;
	MOD(tr[p<<1].mul);
	tr[p<<1|1].mul = tr[p].mul*tr[p<<1|1].mul;
	MOD(tr[p<<1|1].mul);
	
	tr[p].add = 0;
	tr[p].mul = 1;
}
void build(int p,int l,int r){
	tr[p].l = l,tr[p].r = r,tr[p].add = 0,tr[p].mul = 1;
	if(l==r){
		tr[p].sum = a[l];
		return ;
	}
	int mid = (l+r)>>1;
	build(p<<1,l,mid);
	build(p<<1|1,mid+1,r);
	pushup(p);
}
void modify(int p,int l,int r,int add,int mul){
	if(l<=tr[p].l&&r>=tr[p].r){
		tr[p].sum = mul*tr[p].sum + add*(tr[p].r-tr[p].l+1);
		tr[p].add = mul*tr[p].add + add;
		tr[p].mul = mul*tr[p].mul;
		MOD(tr[p].sum);
		MOD(tr[p].mul);
		MOD(tr[p].add);
		return ;
	}
	pushdown(p);
	int mid = (tr[p].l+tr[p].r)>>1;
	if(l<=mid)modify(p<<1,l,r,add,mul);
	if(r>mid)modify(p<<1|1,l,r,add,mul);
	pushup(p);
}
int query(int p,int l,int r){
	if(l<=tr[p].l&&r>=tr[p].r)return tr[p].sum;
	pushdown(p);
	int sum = 0;
	int mid = (tr[p].l+tr[p].r)>>1;
	if(l<=mid)sum += query(p<<1,l,r),MOD(sum);
	if(r>mid)sum += query(p<<1|1,l,r),MOD(sum);
	return sum;
}

signed main(){
	ios::sync_with_stdio(false);
	cin>>n>>m>>mod;
	for(int i=1;i<=n;i++)cin>>a[i];
	build(1,1,n);
	while(m--){
		int op,x,y,k;
		cin>>op>>x>>y;
		if(op==1){
			cin>>k;
			MOD(k);
			modify(1,x,y,0,k);
		}
		if(op==2){
			cin>>k;
			MOD(k);
			modify(1,x,y,k,1);
		}
		if(op==3){
			int sum = query(1,x,y);
			MOD(sum);
			cout<<sum<<"\n";
		}
	}
	return 0;
}

树状数组

以树状数组求逆序对为例
离散化过后置1求和

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 5e5+5;
int tr[N],b[N],a[N],c[N],n;
int lowbit(int x){
	return x&(-x);
}
void update(int p,int x){
	for(;p<=n;p+=lowbit(p))
		tr[p] += x;
}
int query(int p){
	int sum = 0;
	for(;p;p-=lowbit(p)){
		sum += tr[p];
	}
	return sum;
}

signed main(){
	ios::sync_with_stdio(false);
	cin>>n;
	for(int i=1;i<=n;i++)cin>>b[i],c[i] = b[i];
	//离散化
	sort(b+1,b+n+1);
	for(int i=1;i<=n;i++)
		a[i] = lower_bound(b+1,b+n+1,c[i])-b;
	//
	int ans = 0;
	for(int i=1;i<=n;i++){
		update(a[i],1);
		int sum = query(a[i]);
		ans += i-sum;
	}
	cout<<ans<<"\n";
	return 0;
}

树状数组核心操作:

int lowbit(int x){
	return x&(-x);
}

void update(int p,int x){
	for(;p<=n;p+=lowbit(p))
		tr[p] += x;
}

int query(int p){ // sum(tr[0],...tr[p])
	int sum = 0;
	for(;p;p-=lowbit(p)){
		sum += tr[p];
	}
	return sum;
}

堆

优先队列实现
默认是大根堆
priority_queue<int>q;
小根堆:
priority_queue<int,vector<int>,greater<int> >q;

当然也可以像dijkstra那样自定义结构体在结构体里面实现重载运算符
或者自己再写一个cmp结构体重载 ()运算符

单调队列

只要牢记q队列维护的是下标即可

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e6+5;
int n,k,a[N],q[N],l,r;
signed main(){
	ios::sync_with_stdio(false);
	cin>>n>>k;
	for(int i=1;i<=n;i++)cin>>a[i];
	// min
	l = 1,r = 0;
	for(int i=1;i<=n;i++){
		while(l<=r&&a[q[r]]>a[i])r--;
		q[++r] = i;
		while(l<=r&&q[r]-q[l]+1>k)l++;
		if(i>=k)cout<<a[q[l]]<<" ";
	}
	cout<<"\n";
	// max
	l = 1,r = 0;
	for(int i=1;i<=n;i++){
		while(l<=r&&a[q[r]]<a[i])r--;
		q[++r] = i;
		while(l<=r&&q[r]-q[l]+1>k)l++;
		if(i>=k)cout<<a[q[l]]<<" ";
	}
	return 0;
}

单调栈

难的不会 但都要复习下 万一有道简单的单调栈或者思路可以借鉴呢~
以P5788为例 求每个元素之后第一个大于它的元素的下标

跟单调队列一样 记住st栈中存的是元素下标

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 3e6+5;
int n,a[N],st[N],pt,f[N];
signed main(){
	ios::sync_with_stdio(false);
	cin>>n;
	for(int i=1;i<=n;i++)cin>>a[i];
	st[++pt] = 1;
	for(int i=2;i<=n;i++){
		while(a[i]>a[st[pt]]&&pt>0)f[st[pt--]] = i;
		st[++pt] = i;
	}
	for(int i=1;i<=n;i++)cout<<f[i]<<" ";
}

图论

最短路

掌握 Floyd/堆优化的Dijkstra/处理负权的SPFA
借此重新捡起来图论的前向星建图

堆优化Dijkstra

注意vis没用 然后要判断一下 dis[u]!=d 可以大大加速

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5+5;
int n,m,s;
struct Graph{
	int nxt,to,val;
}edge[N<<1];
int head[N],cnt;
void add(int u,int v,int w){
	cnt++;
	edge[cnt].to = v;
	edge[cnt].nxt = head[u];
	edge[cnt].val = w;
	head[u] = cnt;
}
struct did{
	int u,d;
	bool operator < (const did&t)const{
		return t.d<d;
	}
};
priority_queue<did>q;
int dis[N],vis[N];
const int inf = INT_MAX;
void dijkstra(int s){
	for(int i=1;i<=n;i++)dis[i] = inf;
	vis[s] = 1,dis[s] = 0;
	q.push({s,0});
	while(!q.empty()){
		did tmp = q.top();
		q.pop();
		int u = tmp.u,d = tmp.d;
		if(dis[u]!=d)continue; // import optimization!
		for(int i=head[u];i;i=edge[i].nxt){
			int v = edge[i].to;
			int w = edge[i].val;
			if(dis[u]+w<dis[v]){
				dis[v] = dis[u]+w;
				vis[v] = 1;
				q.push({v,dis[v]});
			}
		}
	}
}
signed main(){
	ios::sync_with_stdio(false);
	cin>>n>>m>>s;
	for(int i=1;i<=m;i++){
		int u,v,w;
		cin>>u>>v>>w;
		add(u,v,w);
	}
	dijkstra(s);
	for(int i=1;i<=n;i++)
		cout<<dis[i]<<" ";cout<<"\n";
	return 0;
}

SPFA

万一有负权呐~
同样有些细节要注意 记住spfa本质是bfs 所以要vis判重
最关键的是 vis[u]=0 因为要更新 所以要先置为0

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5+5;
const int inf = LONG_LONG_MAX;
struct Graph{
	int nxt,to,val;
}edge[N<<1];
int n,m,s;
int head[N],cnt;
void add(int u,int v,int w){
	cnt++;
	edge[cnt].to = v;
	edge[cnt].nxt = head[u];
	edge[cnt].val = w;
	head[u] = cnt;
}
int vis[N],dis[N];
queue<int>q;
void spfa(int s){
	for(int i=1;i<=n;i++)dis[i] = inf;
	dis[s] = 0,vis[s] = 1;
	q.push(s);
	while(!q.empty()){
		int u = q.front();
		q.pop();
		vis[u] = 0; // !!!
		for(int i=head[u];i;i=edge[i].nxt){
			int v = edge[i].to;
			int w = edge[i].val;
			if(dis[u]+w<dis[v]){
				dis[v] = dis[u]+w;
				if(!vis[v]){
					vis[v] = 1;
					q.push(v);
				}
			}
		}
	}
}
signed main(){
	ios::sync_with_stdio(false);
	cin>>n>>m>>s;
	for(int i=1;i<=m;i++){
		int u,v,w;
		cin>>u>>v>>w;
		add(u,v,w);
	}
	spfa(s);
	for(int i=1;i<=n;i++)
		cout<<dis[i]<<" ";cout<<"\n";
	return 0;	
}

Floyd

以医院设置为例
注意点:

1. 初始化赋inf
2. g[i][i] = 0
3. 先枚举k

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e2+5;
const int inf = LONG_LONG_MAX;
int a[N],g[N][N],n;
signed main(){
	ios::sync_with_stdio(false);
	cin>>n;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			g[i][j] = 100000;
	for(int i=1;i<=n;i++){
		g[i][i] = 0;
		int l,r;
		cin>>a[i]>>l>>r;
		if(l>0)g[i][l] = g[l][i] = 1;
		if(r>0)g[i][r] = g[r][i] = 1;
	}
	for(int k=1;k<=n;k++)
		for(int i=1;i<=n;i++){
			if(i!=k){
				for(int j=1;j<=n;j++)
					if(j!=k&&j!=i)
						g[i][j] = min(g[i][j],g[i][k]+g[k][j]);
			}
		}
			
	int minn = inf;
	for(int i=1;i<=n;i++){
		int cost = 0;
		for(int j=1;j<=n;j++)
			cost += g[i][j]*a[j];
		minn = min(minn,cost);
	}
	cout<<minn<<"\n";
	return 0;
}

MST

模板:
几个注意点:

1. 并查集的fa[]初始化
2. 不是用前向星建边 本质是记录的边的两个端点
3. 结束条件: \(num == n-{连通块个数}\)

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 5e3+5;
const int M = 2e5+5;
int n,m;
struct Graph{
	int nxt,to,val;
}edge[M<<1];
bool cmp(Graph x,Graph y){
	return x.val<y.val;
}
int fa[N];
int getfa(int x){
	if(fa[x]==x)return x;
	return fa[x] = getfa(fa[x]);
}
void uni(int x,int y){
	int fx = getfa(x),fy = getfa(y);
	fa[fx] = fy;
}

int kruskal(){
	sort(edge+1,edge+m+1,cmp);
	int num = 0,sum_mst = 0;
	for(int i=1;i<=m;i++){
		int u = edge[i].nxt,v = edge[i].to,w = edge[i].val;
		if(getfa(u)==getfa(v))continue;
		num++;
		sum_mst += w;
		uni(u,v);
		if(num==n-1)return sum_mst;
	}
	return 0;
}
signed main(){
	ios::sync_with_stdio(false);
	cin>>n>>m;
	for(int i=1;i<=n;i++)fa[i] = i;
	for(int i=1;i<=m;i++){
		int u,v,w;
		cin>>u>>v>>w;
		edge[i].nxt = u;
		edge[i].to = v;
		edge[i].val = w;
	}
	int ans = kruskal();
	if(!ans)cout<<"orz\n";
	else cout<<ans<<"\n";
	return 0;
}

拓扑排序

以P1960为例
topsort关键流程:

1. 根据题目建图连边
2. 统计入度
3. 初始寻找一遍入度为0的dian
4. 输出queue.front() 然后把与之相连的点度-1 继续找度为0的点
5. 多解情况判断: 某次找度为0的点时有>1个

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
int n,m;
struct Graph{
	int nxt,to,val;
}edge[N<<1];
int head[N],cnt;
void add(int u,int v){
	cnt++;
	edge[cnt].to = v;
	edge[cnt].nxt = head[u];
	head[u] = cnt;
}
int in[N]; // in-degree
queue<int>ans;
int flag = 0; // Multi-Ans
void tpsort(){
	int t = 0;
	for(int i=1;i<=n;i++){
		if(in[i]==0){
			ans.push(i);
			t++;
		}
	}
	if(t>1)flag = 1;
	t = 0;
	while(!ans.empty()){
		int u = ans.front();
		ans.pop();
		cout<<u<<"\n";
		for(int i=head[u];i;i=edge[i].nxt){
			int v = edge[i].to;
			in[v]--; // for all v that directly connected to u
			if(in[v]==0){
				ans.push(v);
				t++;
			}
		}
		if(t>1)flag = 1;
		t = 0;
	}
	cout<<flag<<"\n";
}

signed main(){
	ios::sync_with_stdio(false);
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		int u,v;
		cin>>u>>v;
		add(u,v);
		in[v]++;
	}
	tpsort();
	return 0;
}

欧拉路径(回路)

https://www.cnblogs.com/NozoMizo/articles/17337290.html
https://www.cnblogs.com/NozoMizo/articles/17347676.html
一笔画即为欧拉路径 起点==终点: 欧拉回路
由于都有字典序要求 所以用vector实现

有向图

要注意dfs中 要设定cur[u] 不然死循环了...

#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+5;
int n,m;
vector<int>G[N];
int in[N],out[N],cnt1,cnt2;
stack<int>st;
int cur[N];
void dfs(int u){
	for(int i=cur[u];i<G[u].size();i=cur[u]){
		cur[u] = i+1;
		dfs(G[u][i]);
	}

	st.push(u);
}
signed main(){
	ios::sync_with_stdio(false);
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		int u,v;
		cin>>u>>v;
		G[u].push_back(v);
		in[v]++,out[u]++;
	}
	for(int i=1;i<=n;i++)
		sort(G[i].begin(),G[i].end());
	int is_loop = 1;
	int start = 1;
	for(int i=1;i<=n;i++){
		if(in[i]!=out[i])//not loop
		{
			is_loop = 0;
			if(out[i]==in[i]+1){
				start = i;
				cnt1++;
			}
			else if(in[i]==out[i]+1){
				cnt2++;
			}
			else{
				cout<<"No\n";
				return 0;
			}
			
		}
	}
	if(is_loop==0&!(cnt1==1&&cnt2==1)){
		cout<<"No\n";
		return 0;
	}
	dfs(start);
	while(!st.empty()){
		cout<<st.top()<<" ";
		st.pop();
	}
}

无向图

注意与有向图不同的判定条件

这道题还有个注意点: 遍历的不是 1~n 是 1~125 因为我们图的节点选的是字母的chr
这里dfs的本质就是模拟走一遍 走一条边删一条 然后入栈

#include<bits/stdc++.h>
using namespace std;
const int N = 1e3+5;
int n,m;
vector<int>G[N];
int vis[N][N];
int deg[N];
int fa[N];
stack<int>st;
int getfa(int x){
	if(fa[x]==x)return x;
	return fa[x] = getfa(fa[x]);
}
void uni(int x,int y){
	int fx = getfa(x),fy = getfa(y);
	fa[fx] = fy;
}
void dfs(int u){
	for(int i=1;i<=125;i++){
		if(vis[u][i]){
			vis[u][i] = vis[i][u] = 0;
			dfs(i);
		}
	}
	st.push(u);
}
signed main(){
	ios::sync_with_stdio(false);
	cin>>n;
	for(int i=1;i<=125;i++)fa[i] = i;
	for(int i=1;i<=n;i++){
		string s;
		cin>>s;
		G[s[0]].push_back(s[1]);
		G[s[1]].push_back(s[0]);
		vis[s[1]][s[0]] = vis[s[0]][s[1]] = 1;
		deg[s[0]]++,deg[s[1]]++;
		uni(s[0],s[1]);
	}
	int root_cnt = 0;
	for(int i=1;i<=125;i++)
		if(deg[i]&&fa[i]==i)
			root_cnt++;
	if(root_cnt!=1){
		cout<<"No Solution\n";
		return 0;
	}
	for(int i=1;i<=n;i++)
		sort(G[i].begin(),G[i].end());
	int cntj = 0,start=-1,is_loop = 1;
	for(int i=1;i<=125;i++){
		if(deg[i]!=0&&deg[i]%2==1){
			cntj++;
			is_loop = 0;
			if(start==-1)start = i;
		}
	}
	if(cntj>0&&cntj!=2){
		cout<<"No Solution\n";
		return 0;
	}
	if(is_loop){
		for(int i=1;i<=125;i++)
			if(deg[i]){
				start = i;
				break;
			}
	}
	dfs(start);
	while(!st.empty()){
		cout<<char(st.top())<<"";
		st.pop();
	}
}

差分约束系统

虽说感觉变形变难后也套不对 但是骗分总比不会好...
用来高效求解不等式组
https://www.cnblogs.com/NozoMizo/articles/17321902.html

要点:

• 建立超级源点
• SPFA(...)
• 判负环

两种建模区别:
一般求最早跑最长路 反正都写一写 哪个跟样例一样就哪个...

最短路版:

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m;
const int N = 5e3+5;
const int M = 5e3+5;
const int inf = INT_MAX;
struct Graph{
	int nxt,to,val;
}edge[M<<1];
int head[N],cnt;
void add(int u,int v,int w){
	cnt++;
	edge[cnt].to = v;
	edge[cnt].val = w;
	edge[cnt].nxt = head[u];
	head[u] = cnt;
}
int vis[N],dis[N],in[N];
bool spfa(int s){
	for(int i=0;i<=n+1;i++)dis[i] = inf;
	queue<int>q;
	q.push(s);
	dis[s] = 0;vis[s] = 1;
	while(!q.empty()){
		int u = q.front();
		q.pop();
		vis[u] = 0;
		for(int i=head[u];i;i=edge[i].nxt){
			int v = edge[i].to;
			int w = edge[i].val;
			if(dis[u]+w<dis[v]){
				dis[v] = dis[u]+w;
				if(!vis[v]){
					vis[v] = 1;
					q.push(v);
					in[v]++;
					if(in[v]>n+1)return false;
				}
			}
		}
	}
	return true;
}
signed main(){
	ios::sync_with_stdio(false);
	cin>>n>>m;
	for(int i=1;i<=n;i++)add(0,i,0);
	for(int i=1;i<=m;i++){
		int u,v,w;
		cin>>u>>v>>w;
		add(v,u,w);
	}
	int pd = spfa(0);
	if(pd==false)cout<<"NO\n";
	else {
		for(int i=1;i<=n;i++)
			cout<<dis[i]<<" ";
		cout<<"\n";
	}
	return 0;
}

最长路版

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m;
const int N = 5e3+5;
const int M = 5e3+5;
const int inf = INT_MAX;
struct Graph{
	int nxt,to,val;
}edge[M<<1];
int head[N],cnt;
void add(int u,int v,int w){
	cnt++;
	edge[cnt].to = v;
	edge[cnt].val = w;
	edge[cnt].nxt = head[u];
	head[u] = cnt;
}
int vis[N],dis[N],in[N];
bool spfa(int s){
	for(int i=0;i<=n+1;i++)dis[i] = -inf;
	queue<int>q;
	q.push(s);
	dis[s] = 0;vis[s] = 1;
	while(!q.empty()){
		int u = q.front();
		q.pop();
		vis[u] = 0;
		for(int i=head[u];i;i=edge[i].nxt){
			int v = edge[i].to;
			int w = edge[i].val;
			if(dis[u]+w>dis[v]){
				dis[v] = dis[u]+w;
				if(!vis[v]){
					vis[v] = 1;
					q.push(v);
					in[v]++;
					if(in[v]>n+1)return false;
				}
			}
		}
	}
	return true;
}
signed main(){
	ios::sync_with_stdio(false);
	cin>>n>>m;
	for(int i=1;i<=n;i++)add(0,i,0);
	for(int i=1;i<=m;i++){
		int u,v,w;
		cin>>u>>v>>w;
		add(u,v,-w);
	}
	int pd = spfa(0);
	if(pd==false)cout<<"NO\n";
	else {
		for(int i=1;i<=n;i++)
			cout<<dis[i]<<" ";
		cout<<"\n";
	}
	return 0;
}

无向图的最小环

用Floyd实现

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m;
const int N = 2e2+5;
const int M = 5e3+5;
const int inf = 1e9;
int dis[N][N],g[N][N];
signed main(){
	ios::sync_with_stdio(false);
	cin>>n>>m;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(i!=j)dis[i][j] = g[i][j] = inf;
	
	for(int i=1;i<=m;i++){
		int u,v,w;
		cin>>u>>v>>w;
		dis[u][v] = min(dis[u][v],w);
		dis[v][u] = min(dis[v][u],w);
		g[u][v] = min(g[u][v],w);
		g[v][u] = min(g[v][u],w);
	}
	int minn = inf;
	for(int k=1;k<=n;k++)
	{
		for(int i=1;i<k;i++)
			for(int j=i+1;j<k;j++)
				minn=min(minn,dis[i][j]+g[j][k]+g[k][i]);
		
		for(int i=1;i<=n;i++)
			for(int j=1;j<=n;j++)
				if(i!=j&&j!=k)
					dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]),dis[j][i]=dis[i][j];
	}
	if(minn==inf)cout<<"No solution.\n";
	else cout<<minn<<"\n";
	return 0;
}

二分图匹配-匈牙利算法

P3386 https://www.cnblogs.com/NozoMizo/articles/17319920.html
虽说NM复杂度以及邻接矩阵存空间限制死 但是方便简单 懒得去背Dicnic网络流了...
考到了/想到了 就打匈牙利拿点分 拿不完也无妨~

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 505;
int n,m,e;
int g[505][505];
int vis[505],match[505];
bool find(int x){
	for(int i=1;i<=m;i++){
		if(!vis[i]&&g[x][i]){
			vis[i] = 1;
			int v = match[i];
			if(v==0 || find(v)){
				match[i] = x;
				return true;
			}
		}
	}
	return false;
}

signed main(){
	ios::sync_with_stdio(false);
	cin>>n>>m>>e;
	for(int i=1;i<=e;i++){
		int u,v;
		cin>>u>>v;
		g[u][v] = 1;
	}
	int ans = 0;
	for(int i=1;i<=n;i++){
		memset(vis,0,sizeof(vis));
		if(find(i))ans++;
	}
	cout<<ans<<"\n";
	return 0;
}

树

树形DP

主要练习一下换根DP和一些简单的DP

换根DP

以医院设置为例
树形DP的几个点:

1. 一般都需要一次dfs预处理dep siz fa 这些数组
2. DP时 注意是在DFS(v,u)之前更新f[]还是之后
   (一般父亲更新儿子在之前 儿子更新父亲在之后)

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e2+5;
int n,a[N];
struct Tree{
	int nxt,to;
}edge[N<<1];
int head[N],cnt,tot;
void add(int u,int v){
	cnt++;
	edge[cnt].to = v;
	edge[cnt].nxt = head[u];
	head[u] = cnt;
}
int dep[N],siz[N],fa[N];
void dfs(int u,int fat){
	fa[u] = fat,dep[u] = dep[fat]+1,siz[u] = a[u];
	for(int i=head[u];i;i=edge[i].nxt){
		int v = edge[i].to;
		if(v==fat)continue;
		dfs(v,u);
		siz[u] += siz[v];
	}
}
int f[N];
void DFS(int u,int fat){
	for(int i=head[u];i;i=edge[i].nxt){
		int v = edge[i].to;
		if(v==fat)continue;
		f[v] = min(f[v],f[u]+tot-2*siz[v]);
		DFS(v,u);
	}
}
signed main(){
	ios::sync_with_stdio(false);
	cin>>n;
	for(int i=1; i<=n; i++) {
		int u,v;
		cin>>a[i];
		tot+=a[i];
		cin>>u>>v;
		if(u)add(i,u),add(u,i);
		if(v)add(i,v),add(v,i);
	}
	memset(f,0x3f,sizeof(f));
	dfs(1,0);
	f[1] = 0;
	for(int i=2;i<=n;i++)f[1] += a[i]*(dep[i]-dep[1]);
	DFS(1,0);
	int minn = LONG_MAX;
	for(int i=1;i<=n;i++)minn = min(minn,f[i]);
	cout<<minn<<"\n";
	return 0;
}

LCA

树链剖分版
借此熟悉树的相关操作 儿子节点和父节点的关系以及其对应的前向星建树
注意几个点:

1. for(int i=1;i<n;i++)cin>>u>>v;
2. if(v==fat)continue
3. 实际上是 dfs1(root,0) dfs2(root,root)

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e4+5;
int n;
struct Graph{
	int nxt,to;
}edge[N<<1];
int head[N],cnt;
void add(int u,int v){
	cnt++;
	edge[cnt].to = v;
	edge[cnt].nxt = head[u];
	head[u] = cnt;
}
int dep[N],siz[N],son[N],fa[N],wid[N],maxwid,maxdep;
void dfs1(int u,int fat){
	dep[u] = dep[fat]+1,fa[u] = fat,siz[u] = 1,wid[dep[u]]++;
	maxwid = max(maxwid,wid[dep[u]]);
	maxdep = max(maxdep,dep[u]);
	int maxson = -1;
	for(int i=head[u];i;i=edge[i].nxt){
		int v = edge[i].to;
		if(v==fat)continue;
		dfs1(v,u);
		siz[u] += siz[v];
		if(siz[v]>maxson)maxson = siz[v],son[u] = v;	
	}
}
int id[N],times = 0,top[N];
void dfs2(int u,int topf){
	id[u] = ++times;
	top[u] = topf;
	if(!son[u])return ;
	dfs2(son[u],topf);
	for(int i=head[u];i;i=edge[i].nxt){
		int v = edge[i].to;
		if(id[v])continue;
		dfs2(v,v);
	}
}
int LCA(int x,int y){
	while(top[x]!=top[y]){
		if(dep[top[x]]<dep[top[y]])swap(x,y);
		x = fa[top[x]];
	}
	if(dep[x]>dep[y])swap(x,y);
	return x;
}
signed main(){
	ios::sync_with_stdio(false);
	cin>>n;
	for(int i=1;i<n;i++){
		int u,v;
		cin>>u>>v;
		add(u,v);
		add(v,u);
	}
	dfs1(1,1);
	dfs2(1,1);
	int x,y;
	cin>>x>>y;
	cout<<maxdep<<"\n"<<maxwid<<"\n";
	int u = LCA(x,y);
	int ans = 2*(dep[x]-dep[u])+(dep[y]-dep[u]);
	cout<<ans<<"\n";
	return 0;
}

树上差分

与LCA结合的题目

点差分

统计的是节点的情况
处理:

int u = LCA(s,t);
chafen[s]++,chafen[t]++;
chafen[u]--,chafen[fa[u]]--;

最后跑一遍dfs把chafen[]累加起来就ok

#include<bits/stdc++.h>
using namespace std;
const int N = 5e4+4;
const int M = 1e5+5;
int n,m;
struct Tree{
	int nxt,to;
}edge[N<<1];
int head[N],cnt;
void add(int u,int v){
	cnt++;
	edge[cnt].to = v;
	edge[cnt].nxt = head[u];
	head[u] = cnt;
}
int fa[N],dep[N],siz[N],son[N];
void dfs1(int u,int fat){
	fa[u] = fat,dep[u] = dep[fat]+1,siz[u] = 1;
	int maxson = -1;
	for(int i=head[u];i;i=edge[i].nxt){
		int v = edge[i].to;
		if(v==fat)continue;
		dfs1(v,u);
		siz[u] += siz[v];
		if(siz[v]>maxson)maxson = siz[v],son[u] = v;
	}
}
int top[N],id[N],idx = 0;
void dfs2(int u,int topf){
	id[u] = ++idx;
	top[u] = topf;
	if(!son[u])return ;
	dfs2(son[u],topf);
	for(int i=head[u];i;i=edge[i].nxt){
		int v = edge[i].to;
		if(id[v])continue;
		dfs2(v,v);
	}
}
int LCA(int x,int y){
	while(top[x]!=top[y]){
		if(dep[top[x]]<dep[top[y]])swap(x,y);
		x = fa[top[x]];
	}
	if(dep[x]>dep[y])swap(x,y);
	return x;
}
int chafen[N];
void dfs(int u,int fat){ // to sum up  chafen[]
	for(int i=head[u];i;i=edge[i].nxt){
		int v = edge[i].to;
		if(v==fat)continue;
		dfs(v,u);
		chafen[u] += chafen[v];
	}
}
signed main(){
	ios::sync_with_stdio(false);
	cin>>n>>m;
	for(int i=1;i<n;i++){
		int u,v;
		cin>>u>>v;
		add(u,v);
		add(v,u);
	}
	dfs1(1,0);
	dfs2(1,1);
	for(int i=1;i<=m;i++){
		int s,t;
		cin>>s>>t;
		int u = LCA(s,t);
		chafen[s]++,chafen[t]++;
		chafen[u]--,chafen[fa[u]]--;
	}
	dfs(1,0);
	int maxflow = -1;
	for(int i=1;i<=n;i++)maxflow = max(maxflow,chafen[i]);
	cout<<maxflow<<"\n";
	return 0;
}

边差分

将边经过的次数问题转化为子节点
比如 u->v 就转化到 chafen[v]
那么如果要用到edge[]的信息怎么找u对应哪条边呢?
我们枚举u的邻接点v 如果v==fat 就把这条边i记录下来
然后累加完得到chafen[u] 就可以利用i这条边上存储的信息解个chafen[u]存储的i经过的次数来解题了
以 P6869 为例

#include<bits/stdc++.h>
using namespace std;
const int N = 200000+5;
const int M = 1e5+5;
int n;
struct Tree{
	int nxt,to,w1,w2;
}edge[N<<1];
int head[N],cnt;
void add(int u,int v,int w1,int w2){
	cnt++;
	edge[cnt].to = v;
	edge[cnt].nxt = head[u];
	edge[cnt].w1 = w1;edge[cnt].w2 = w2;
	head[u] = cnt;
}
int fa[N],dep[N],siz[N],son[N];
void dfs1(int u,int fat){
	fa[u] = fat,dep[u] = dep[fat]+1,siz[u] = 1;
	int maxson = -1;
	for(int i=head[u];i;i=edge[i].nxt){
		int v = edge[i].to;
		if(v==fat)continue;
		dfs1(v,u);
		siz[u] += siz[v];
		if(siz[v]>maxson)maxson = siz[v],son[u] = v;
	}
}
int top[N],id[N],idx = 0;
void dfs2(int u,int topf){
	id[u] = ++idx;
	top[u] = topf;
	if(!son[u])return ;
	dfs2(son[u],topf);
	for(int i=head[u];i;i=edge[i].nxt){
		int v = edge[i].to;
		if(id[v])continue;
		dfs2(v,v);
	}
}
int LCA(int x,int y){
	while(top[x]!=top[y]){
		if(dep[top[x]]<dep[top[y]])swap(x,y);
		x = fa[top[x]];
	}
	if(dep[x]>dep[y])swap(x,y);
	return x;
}
int chafen[N];
long long tot = 0;
void dfs(int u,int fat){
	int x;
	for(int i=head[u];i;i=edge[i].nxt){ // essentially, what i record is the edge
		int v = edge[i].to;
		if(v==fat){
			x = i;
			continue;
		}
		else{
			dfs(v,u);
			chafen[u] += chafen[v];
		}
	}
	tot += min((long long)((long long)edge[x].w1*(long long)(chafen[u])),(long long)(edge[x].w2));
}
signed main(){
	ios::sync_with_stdio(false);
	cin>>n;
	for(int i=1;i<n;i++){
		int u,v,w1,w2;
		cin>>u>>v>>w1>>w2;
		add(u,v,w1,w2);
		add(v,u,w1,w2);
	}
	dfs1(1,0);
	dfs2(1,1);
	for(int i=1;i<n;i++){
		int s = i,t = i+1;
		int u = LCA(s,t);
		chafen[s]++,chafen[t]++;
		chafen[u] -= 2;
	}
	dfs(1,0);
	cout<<tot<<"\n";
	return 0;
}

树的直径

两次dfs求出直径
以P5536为例
dfs1随便以一个点作为root跑出一条最长pos记录另一端点
然后以这个端点再同样dfs2一次 这样就找到了树的直径 然后取直径的中间点建核心城市即可

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+5;
int n,k;
struct Tree {
	int nxt,from,to,val;
} edge[N<<1];
int head[N],cnt;
int root;
inline void add(int u,int v) {
	cnt++;
	edge[cnt].to=v;
	edge[cnt].from=u;
	edge[cnt].nxt=head[u];
	head[u]=cnt;
}
int num,dep[N],zj,fa[N];
void dfs1(int u,int fat) {
	if(u!=root)
		dep[u]=dep[fat]+1;
	if(dep[u]>zj) {
		zj=dep[u];
		num=u;
	}
	for(int i=head[u]; i; i=edge[i].nxt) {
		int v=edge[i].to;
		if(v==fat)continue;
//		dep[v]=dep[u]+1;
		dfs1(v,u);
	}
}
int f[N];
void dfs2(int u,int fat) {
	if(u!=root)
		dep[u]=dep[fat]+1;
	if(dep[u]>zj) {
		zj=dep[u];
		num=u;
	}
	for(int i=head[u]; i; i=edge[i].nxt) {
		int v=edge[i].to;
		if(v==fat)continue;
//		dep[v]=dep[u]+1;
		f[v]=u;
		dfs2(v,u);
	}
}
int maxdep[N];
int mid;
void dfs3(int u,int fat) {
	if(u!=mid)
		maxdep[u]=1;
	for(int i=head[u]; i; i=edge[i].nxt) {
		int v=edge[i].to;
		if(v==fat)continue;
		dfs3(v,u);
		maxdep[u]=max(maxdep[u],maxdep[v]+1);
	}
}
bool cmp(int x,int y) {
	return x>y;
}
signed main() {
	ios::sync_with_stdio(false);
	cin>>n>>k;
	for(int i=1; i<n; i++) {
		int u,v;
		cin>>u>>v;
		add(u,v);
		add(v,u);
	}
	zj=0,num=-1;
	memset(dep,0,sizeof(dep));
	root=1;
	dfs1(1,0);
	memset(dep,0,sizeof(dep));
	zj=0;
	root=num;
	dfs2(num,0);
	mid=num;
	for(int i=1; i<=(zj+1)/2; i++)mid=f[mid];
	dfs3(mid,0);
	sort(maxdep+1,maxdep+n+1,cmp);
	cout<<maxdep[k+1]<<"\n";
	return 0;
}

字符串

字典树

用于快速计算对于多个给的模式串t 给定的n个s中有多少个满足以t为前缀
就是建了一个多叉树 然后维护父节点的cnt
注意别用memset 因为前一次只用了idx个 所以for循环清空到idx即可!大大提升效率

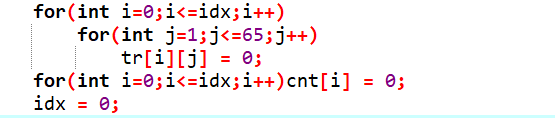
#include<bits/stdc++.h>
using namespace std;
//#define int long long
const int N = 3e6+5;
int tr[N][65],cnt[N];
int T,n,q;
int idx = 0;
int getnum(char ch){
	if(ch>='A'&&ch<='Z')return ch-'A'+1;
	if(ch>='a'&&ch<='z')return ch-'a'+1+26;
	if(ch>='0'&&ch<='9')return ch-'0'+1+26+26;
}
void insert(string s){
	int l = s.size();
	int p = 0;
	for(int i=0;i<l;i++){
		int c = getnum(s[i]);
		if(!tr[p][c])
			tr[p][c] = ++idx;
		p = tr[p][c];
		cnt[p]++;
	}
}
int query(string s){
	int l = s.size();
	int p = 0;
	for(int i=0;i<l;i++){
		int c = getnum(s[i]);
		if(!tr[p][c])return 0;
		p = tr[p][c];
	}
	return cnt[p];
}
signed main(){
	ios::sync_with_stdio(false);
	cin>>T;
	while(T--){
		for(int i=0;i<=idx;i++)
			for(int j=1;j<=65;j++)
				tr[i][j] = 0;
		for(int i=0;i<=idx;i++)
			cnt[i] = 0;
		idx = 0;
		cin>>n>>q;
		for(int i=1;i<=n;i++){
			string s;
			cin>>s;
			insert(s);
		}
		while(q--){
			string s;
			cin>>s;
			cout<<query(s)<<"\n";
		}
	}
}

KMP

字符串类型的题目部分分就靠这个算法了

求s2在s1中出现的 位置/次数
复杂度从暴力的O(n*m)优化到O(n+m)
两次过程很像 注意区别+联系
f[i]==l2就是匹配的条件 出现的位置就是 i-l2+1

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e6+5;
int nxt[N],f[N];
string s1,s2;
signed main(){
	ios::sync_with_stdio(false);
	cin>>s1>>s2;
	int l1 = s1.size(),l2 = s2.size();
	s1 = " "+s1,s2 = " "+s2;
	nxt[1] = 0;
	for(int i=2,j=0;i<=l2;i++){
		while(j>0&&(j==l2||s2[i]!=s2[j+1]))j = nxt[j];
		if(s2[i]==s2[j+1])j++;
		nxt[i] = j;
	}
	
	for(int i=1,j=0;i<=l1;i++){
		while(j>0&&(j==l2||s1[i]!=s2[j+1]))j = nxt[j];
		if(s1[i]==s2[j+1])j++;
		f[i] = j;
		if(f[i]==l2)
			cout<<i-l2+1<<"\n";
	}
	for(int i=1;i<=l2;i++)cout<<nxt[i]<<" ";cout<<"\n";
	return 0;
}

DP/贪心/分治

数论

线性筛素数

注意几个地方的优化细节

#include<bits/stdc++.h>
using namespace std;
void write(int x){
	if(x<0)putchar('-'),x = -x;
	if(x>9)write(x/10);
	putchar(x%10+'0');
}
int n;
const int N = 1e6+5;
bool notp[N];
int prime[N],cntp;
void work(int n){
	notp[1] = 1;
	for(int i=2;i<=n;i++){
		if(!notp[i])prime[++cntp] = i;
		for(int j=1;j<=cntp;j++){
			if(prime[j]*i>n)break;
			notp[prime[j]*i] = 1;
			if(i%prime[j]==0 || prime[j]%i==0)break;
		}
	}
}
signed main(){
	scanf("%d",&n);
	work(n);
	for(register int i=1;i<=cntp;i++){
		write(prime[i]);
		putchar(' ');
	}
}

扩展欧几里得算法

exgcd:
密码学python套过很多次模板...

#include<bits/stdc++.h>
using namespace std;
int xx = 0,yy = 0;
int exgcd(int a,int b){
	if(b==0){
		xx = 1,yy = 0;
		return a;
	}
	int GCD = exgcd(b,a%b);
	int tmp = xx;
	xx = yy;
	yy = tmp-a/b*yy;
	return GCD;
}
/*
to calculate the x satisfy that a*x === 1 mod m
we just change the equivalent to this form:
ax + b*m == 1
so we use exgcd(a,m) => x,b
*/
signed main(){
	ios::sync_with_stdio(false);
	int a,m;
	cin>>a>>m;
	int gcd = exgcd(a,m);
	while(xx<0)
		xx += m;
	yy = (1-a*xx)/m;
	cout<<xx<<" "<<yy<<"\n";
	return 0;
}

卢卡斯定理

快速组合数求模

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m,p;
int qpow(int a,int b,int c){
	int tmp = 1;
	while(b){
		if(b&1)tmp = ((tmp*a)%c+c)%c;
		a = ((a*a)%c+c)%c;
		b>>=1;
	}
	return tmp;
}
int C(int n,int m){
	if(n<m)return 0;
	if(m>n-m)m = n-m;
	int a=1,b=1;
	for(int i=0;i<m;i++){
		a = (a*(n-i))%p;
		b = (b*(i+1))%p;
	}
	return a*qpow(b,p-2,p)%p;
}
int Lucas(int n,int m){
	if(m==0)return 1;
	return Lucas(n/p,m/p)*C(n%p,m%p)%p;
}
signed main(){
	ios::sync_with_stdio(false);
	int T;
	cin>>T;
	while(T--){
		cin>>n>>m>>p;
		int ans = Lucas(n+m,m);
		cout<<((ans%p)+p)%p<<"\n";
	}
	return 0;
}

其它

高精度

不是我说 这好久没自己写过了... 如果真考了不复习就gg... 绝对心态调炸...
写的时候不要管什么规范接口方便调用之类的 跑起来才是第一位的...

Hanoi双塔

高精x单精

#include<bits/stdc++.h>
using namespace std;
int n;
int a[100005],l1;
void gjc(int x){
	int l = l1,jw = 0;
	for(int i=1;i<=l+1;i++){
		a[i] = (a[i]*x+jw);
		jw = a[i]/10;
		a[i] %= 10;
	}
	if(a[l+1]!=0)l++;
	l1 = l;
}
signed main(){
	ios::sync_with_stdio(false);
	// 2**(n+1)-2
	cin>>n;
	a[++l1] = 1;
	for(int i=1;i<=n+1;i++){
		gjc(2);
//		for(int j=l1;j>=1;j--)cout<<a[j];
//		cout<<"\n";
	}
	for(int i=l1;i>=2;i--)cout<<a[i];
	cout<<a[1]-2<<"\n";
	return 0;
}

最大乘积

其实这题拆分方法很容易想错...

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,c=1;
int nn = 0,jl[100050];
int a[400050],l = 1;
void gjc(int x){
	int jw = 0;
	for(int i=1;i<=l+9;i++){
		a[i] = (a[i]*x+jw);
		jw = a[i]/10;
		a[i] %= 10;
	}
	jw = 0;
	for(int i=l;i<=l+20;i++){
		a[i] = a[i]+jw;
		jw = a[i]/10;
		a[i] %= 10;
	}
	for(int i=l+20;i;i--){
		if(a[i]!=0){
			l = i;
			break;
		}
	}
	
}
signed main(){
	ios::sync_with_stdio(false);
	cin>>n;
	if ( n <= 4 ){
        printf ( "%d\n%d\n", n, n );
        return 0;
    }
    for ( int i = 2; i <= n; i++ ){
        if ( n >= i )
        n -= i, jl[c++] = i;
        else break;
    }
    for ( int i = c - 1; i >= 1; i-- )
    if ( n > 0 ) jl[i]++, n--;
    if ( n > 0 ) jl[c-1]++;
	for(int i=1;i<c;i++)cout<<jl[i]<<" ";cout<<"\n";
	a[1] = 1;
	for(int i=1;i<c;i++){
		gjc(jl[i]);
	}
	for(int i=l;i>=1;i--)cout<<a[i];
	cout<<"\n";
	return 0;
}