小完能干脆面

 

题目描述

 

---

 

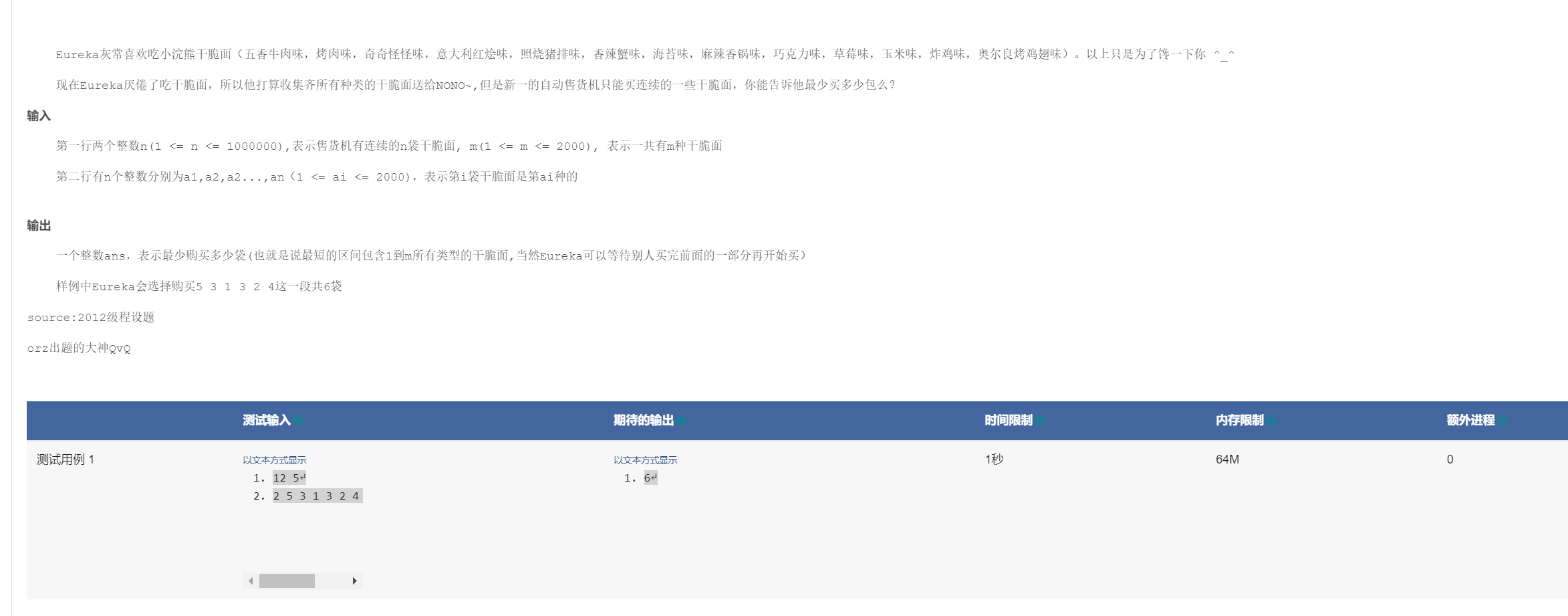
思路

数据量有一百万，从时间复杂度分析，应该是O(n)或顶多O(n*log(n))

（1）错误思路   O(n*log(n))的算法考虑，二分长度进行检验，O(log(n))的二分长度，O(n)的检验，欲实现O(n)的检验，还需要前缀和处理一下

int sum[1000009][2009] ;
//sum[i][j] 表示前 i 位中 j 号干脆面的数量
//sum[right][j]-sum[left-1][j] 表示left到right的闭区间中的 j 号干脆面的数量

　　但这样肯定MLE，这个思路可以参考，但不够优

（2）正解     

采用双指针，cnt1指区间左端点，cnt2指区间右端点，贪心维护每个左端点能包含所有种类干脆面的最短区间

详细解释

用 num[i] 表示在 [ cnt1 , cnt2 ] 区间内的 i 号干脆面数量

初始时刻cnt1,cnt2均在 1 位置，此时干脆面种类不全，右指针cnt2左移，同时加上对应cnt2位置上的干脆面

//左移，并加上对应区域的干脆面
cnt2 ++ ;
num[ a[cnt2] ] ++ ;//cnt2 表示指针的位置，a[ cnt2 ] 是对应位置的干脆面种类
//num[ a[cnt2] ] 就表示cnt2位置上的干脆面型号加一

　每次cnt2 右移后，加上对应位置的干脆面，并进行一次检查，检查干脆面种类是否齐全，如果齐全则移动左指针，并抛弃原左指针位置的干脆面

　初始时刻，cnt1 = 1 ,由于干脆面型号不齐全， cnt2 会一直向右移动，不断加上 对应位置上的干脆面型号  ，直到齐集所有型号干脆面

集齐所有干脆面后，左指针cnt1 开始向右移动，在开始移动前更新以cnt1 为起点的 包含所有干脆面型号的 最小区间长度，并抛弃原位置的干脆面

num[ a[cnt1] ]-- ;//此时左指针未移动，cnt1 对应位置的干脆面型号减一
cnt1 ++ ;//注意是先减干脆面型号数量，再左移，因为 cnt1 位置是闭区间

　贪心维护长度，刚好包含所有干脆面时，左指针位置到右指针位置的区间长度必定是最小的

 len[cnt1] = cnt2-cnt1+1 ;//更新以cnt1 为起点的包含所有干脆面的最小区间长度

然后不断右移左指针，直到干脆面不齐全，然后又开始移动右指针

不断重读以上操作，直到右指针cnt2 到达整个区间的右端点

题外话

关于检查是否集齐所有干脆面这里可以有优化，不需要每次全部检查一遍干脆面的型号

在第一次发现干脆面集齐后，只需要检查左指针cnt1移动抛弃的干脆面型号是否为0即可（因为对于一个集齐干脆面的区间，因为左指针移动而不齐，只可能是刚才抛弃的型号引起）

由于不用优化就能过，代码部分就从简了

---

 

代码实现

#include<stdio.h>
#include<string.h>
#include<iostream>
#include<math.h>
#include<cmath>
#define MAXN 1000009 
int a[MAXN] , len[MAXN] , cnt1 = 1 , cnt2 = 1 ;//a记录对应位置的干脆面型号，len记录以左端点i为起点的最小区间长度
int n , m , ans = MAXN ;//ans记录所有的最小区间长度的最小值
int num[2009] ;//记录对应干脆面型号的数量

bool check() {//如果编译出错，就将bool 改为 int 
	for( int i = 1 ; i <= m ; ++ i ) {
		if( !num[i] )
			return 0 ;
	}
	return 1 ;
}

int main() {
	memset(num,0,sizeof(num) );
	scanf("%d%d", &n , &m );
	for( int i = 1 ; i <= n ; ++ i )
		scanf("%d", &a[i] );
	num[a[cnt1]] ++ ;//一号位的干脆面型号+1
	while( cnt2 < n ) {//右指针没到底
		if( !check() )//如果目前的区间没有齐集干脆面
			cnt2 ++ , num[a[cnt2]] ++ ;//右指针右移，将新纳入区间的干脆面型号+1
		else {//如果集齐
			len[cnt1] = cnt2-cnt1+1 ;//先更新长度
			if( ans >= len[cnt1] )
				ans = len[cnt1] ;
			num[a[cnt1]] -- , cnt1 ++ ;//左指针右移
		}
	}
	printf("%d", ans );
}