C++学习笔记：有向图的强连通分量

强连通图分量

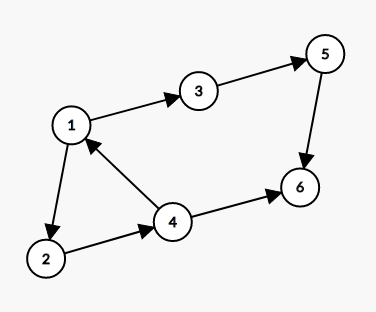
首先得知道这是个什么玩意儿，对于一个如下的有向图

在这个有向图G中，如果有两个点可以相互到达，则两点为强连通，若图中每个点都可以相互到达，则图G为强连通图

1. 一个有向图是强连通的，而且仅当G中有一条回路，它至少包含每个点一次

2. 非强连通图的极大强连通子图，称为强连通分量，孤立的点也是一个强连通分量

（copy课件不解释）

 

---

实现方法

1. Kosaraju算法

（1）首先DFS遍历一遍图，在DFS回溯中标记点，得到一个后序遍历的表

（2）一个原图G的反图R，按 1 中的表DFS遍历

（3）在 2 中，用了多少次DFS，就有多少个强连通分量

为什么可以这样实现，可以理解为如果点 i 和点 j 强连通，则 i 可以到 j，j 可以到 i，则在反图中也可以相互到达

#include <iostream>
#include <cstdio>
#include <cm