C++学习笔记:Tarjan算法剖析——求 强连通分量,割点,割边,点双连通分量,边双连通分量 的详解
Tarjan算法详解
目录
1.Tarjan算法求强连通分量
了解一下 强连通分量
对于一个有向图的DFS的搜索树(i 可以到 j,j 不一定能到 i),如下
里面的强连通分量有 { 6 , 7 , 8 } ,{ 4 } , { 3 } , { 2 } , { 1 } , { 9 }
而强连通分量产生的环 { 6 , 7 , 8 } 是有父子关系的,所以在 { 2 , 3 , 4 , 9 } 这个环不是强连通分量,因为搜索树是有向的(3 , 9 可以到 4 , 而 4 不能访问回去)
在用Tarjan算法时,栈中的点一定是有父子关系的
DFN[ i ] 数组表示遍历到点 i 时DFS的次数
low[ i ] 数组表示点 i 到栈中
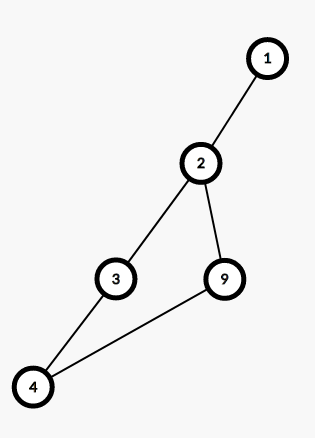
在搜索的过程中会先搜索 1——2——3——4,然后在到 9 的时候就会有这种情况
在用Tarjan算法时,用栈存储的点有 { 1 , 2 , 3 , 9 } ,这时还未遍历点 4,点 4 不在栈中,与点 9 没有父子关系
遍历到点 4 ,此时点 4 无法往下遍历,且与栈中点 9 无父子关系,只能退出栈,有强连通分量 { 4 },然后回溯
依次退栈,有强连通分量 { 3 },{ 9 },{ 2 },{ 1 }
遍历到如下情况
遍历到点 7,栈中的点有 { 5, 6 , 7 }
往下遍历到点 8,栈中点 { 5, 6,7,8 },到点 8 后往下遍历到点 6,点 6 为栈中点,则点 8 到栈中深度最小的点为点 6,low[ 8 ] = 6