C++学习笔记：图论——拆点详解

引言

拆点，玄学的东西，你值的拥有。。。

---

详解

拆点就是将一个图里的边权全部化为 1 ，就要将每一个点拆解为几个点，每个拆解后的点的边权为 1 

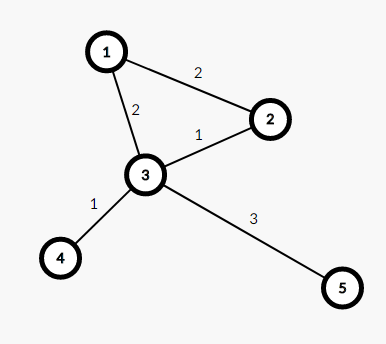
 一个图的邻接矩阵

其中最大的边权为 3 

则每一个点拆分为 i.1 ， i.2 ， i.3 的分点

分点先与自己相邻的分点相连，但要把 i.1 看为原来的点

即 1.1 与 1.2 连

1.2 与 1.3 连

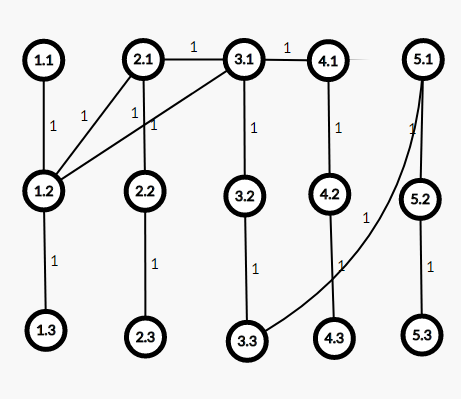
拆完后的图为

点1 到 点2 的边权为 2 

则 1.2 与 2.1 连

点1 到 点3 的边权为 2 

则 1.2 与 3.1 连

以此慢慢连边。。。

最后所得的图为

但是，这个图该怎样构造呢???  我们是把原图的最大的边权作为每个点的分点的个数

那么这个图就有 （最大边权 * 原图点数） 这么多个点

这时候就要把分点看做一个单独的点

就设 1.1 为 点1，1.2 为点2 ，1.3 为 点3，以此类推，那 3.3 这个点应是 点几 呢，他们之间的规律是什么

不难发现对于 i.j 这个点，转化后为 点 ( i-1 ) * maxl + j （maxl 为最大边权）

因为每个原点有 maxl 个分点

则 i.1 就是 点 ( i-1 )*maxl，而 i.j 为原点 i 的第 j 个分点

所以 i.j 这个点，转化后为 点 ( i-1 ) * maxl + j

int rep( int x , int y ) {
    return maxl*(x-1) + y ;
}

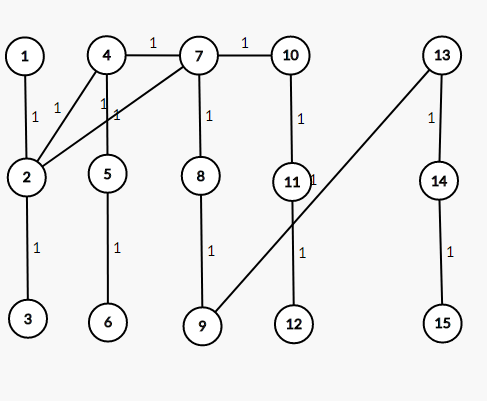
 转化后的图为

然后就是将这个新图连结起来，先把 i.1 与 i.2 相连，i.2 与 i.3 相连

再将原图相连的点连接 ，如果原图点 i 与 j 的边权为 x，则 i.x 与 j.1 相连 

​
for(int i = 1 ; i <= N ; ++ i ) {//N表示点数
        for(int j = 1 ; j < maxl ; ++ j )//maxl最大边权
            G_after[ rep( i,j ) ][ rep( i,j+1 ) ] = 1 ;//G_after存储拆点后的图
        for(int j = 1 ; j <= N ; ++ j ) {
            if( G[i][j] != 0 )//判断原图是否相连
                G_after[ rep( i,G[i][j] )][ rep( j,1 )] = 1 ;//连边
        }//rep返回拆点后的点的编号
    }

​

然后就可以为所欲为了（嘿嘿嘿...）

/*         _    _____         _
           \`,""   ,'7"r-..__/ \
          ,'\/`, ,',','    _/   \
         /   \/ 7 / /     (   \ |
        J     \/ j  L______\  / |
        L   __JF"""/""\"\_,    /
        L,-"| O|  | O |  L_  _/
        F   \_ /  \__/   `-  /|
            .-'    `"""    ,' |          _..====.._
            \__/         r"_  A        ,' _..---.._`,
             `-.______,,-L// / \  ___,' ,'_..:::.. `,`,
                      /   / / / 7"    `-<""=:'  '':. \ \
                     |   <,' /  F  . i , \   `,    :T W I
                     |    \,'  /    >X<  |     \   :| |  L
                     \     `._/    ' ! ` |      I  :| |  G
                      \           \     /       |  :H T  |
                     __>-.__   __,-\   |        |  S P   |
                    /     /|   | \  \  \_       | 'A R   |
                   /   __/ |   |  \  \   \      K./ /   L
                  /   |    |   |  |  |   |     E/ /   ,'
                 |    \    |   |  |  |   |    // / _,'
        _________|     |   |   |  |  |   |   //_/-'
        \   __   |    /    |   | /   |   |  /="
        \\  \_\  \__,' \  /    |/   /    |
        \\\_____________\/     F___/     F
         \\| 计算机编程 |_____/   (_____/
          \/从入门到入土/
*/

---

用到拆点的题

1. 迷路[SCOI2009]