dsu on tree
启发式合并一般是小的往大的合并,可以保证时间复杂度为\(log\)
考虑在解决树上问题的时候也使用相同的思想,这就是树上启发式合并
1.时间复杂度较于暴力优秀的多
2.维护的信息很灵活,但一般只局限与子树问题
3.向上的过程维护的信息不变且集合只增不减
其实现一般都很类似
首先我们考虑维护重儿子的信息,然后在合并的时候将轻儿子的信息暴力的往父亲上合并
这里给出模板
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int MAX = 1e6 + 70;
string S[MAX];
int n, m, fa[MAX], top[MAX], id[MAX];
int bson[MAX], dep[MAX], siz[MAX];
map<string,int> hon;
vector<int> son[MAX];
vector<PII> ask[MAX];
vector<PII> hav[MAX]; // dep, id
map<int, int> mp[MAX];
void pre_dfs(int x, int chain) { //划分轻重链
top[x] = chain;
for(int to : son[x]) {
if(to == bson[x] && bson[x] != n + 10) pre_dfs(to, chain);
else pre_dfs(to, to);
}
}
void dfs_size(int x) { //求重儿子
dep[x] = dep[fa[x]] + 1; siz[x] = 1;
for(int t : son[x]) {
dfs_size(t);
siz[x] += siz[t];
if(siz[t] > siz[bson[x]]) bson[x] = t;
}
}
void dfs(int x) {
for(auto y : son[x]) if(y != bson[x]) dfs(y);
if(bson[x]) dfs(bson[x]);
if(bson[x]) swap(hav[x], hav[bson[x]]);
for(auto y : son[x]) {
if(y != bson[x]) {
for(PII v : hav[y]) {
// bson -> big_son 合并轻儿子
}
}
vector<PII> ttt; swap(ttt, hav[y]);
}
Now =
hav[x].push_back(Now);
/*
维护的信息
*/
for(PII y : ask[x]) {
}
if(x == top[x]) {
for(PII y : hav[x]) { //清空轻子树
}
}
}
int main() {
ios::sync_with_stdio(false);
cin>>n;
dfs_size(1); //预处理重儿子
pre_dfs(1, 0); //划分轻重链
dfs(1); //求解
for(int i = 1; i <= m; i++) {
cout<<ANS[i]<<'\n';
}
return 0;
}
Lomsat gelral
我们考虑如何使用 dsu on tree 解决这个问题,首先题目所求的问题只与子树中的信息有关
考虑如何维护,首先我们暴力的想,如果我们对于每个点都开一个桶,对于每一个点都暴力的扫一遍即可求出答案,但是这样复杂度也就成功爆炸了
我们发现在向上回溯的过程中,相当于儿子的桶不断往父亲的桶上加,假设我们保留一个儿子的桶,让其他儿子都往这个儿子上加效果其实是一样的,那么我们保留重儿子的信息,对于轻儿子的点我们开一个\(vector\)储存一下子树信息,然后往里面加即可
Tree and Queries
对于这个问题,我们同样暴力的思考,
如果我们把询问挂在点上
我们对于每个点都开一个树状数组,即可求出对于这个点的询问,
同样的道理,我们套上dsu on tree 就可以在\(O(nlog_n^2)\)的时间复杂度解决这个问题
Dominant Indices
这个题开始看错了,以为是所有点到\(u\)的距离为\(x\)的节点数,也能做,特判一下就可以了
但是这个题只要求的子树中的点,细节大大减少了,首先我们发现对于每个点都统计到它距离为\(x\)为点未免太过暴力,考虑转化,我们记录\(dep[]\)的点数,然后\(dep[] - dep[x]\)即为一个\(k\),这样我们的集合就只增不减了,套上dsu on tree 即可解决
时间复杂度: \(O(nlog_n)\)
Blood Cousins Return
此题的解决方法和上题一模一样,只要我们记录\(dep[]\)的个数,然后开个\(map\)记录一下名字的个数,对于没有出现过然后出现的点让它所处的层数加一下即可,当然映射一下,可以去掉一个\(log\)
时间复杂度: \(O(nlog_n)\)
Tree Requests
我们发现对于回文串的要求即出现次数为奇数次的字符最多只有一个,
首先我们同样用到上面的套路,改为记录\(dep\),然后暴力插入的时间复杂度太高,我们套上 dsu on tree 即可
时间复杂度\(O(24 n log_n)\)
Arpa’s letter-marked tree and Mehrdad’s Dokhtar-kosh paths
貌似是dsu on tree 的发明者出的题
首先我们观察题面,为什么有\(26\)个字符题目却只给了\(22\)个?
那么就是在暗示你给出一个含有\(2^{22}\)的解决方式
我们发现一条路径的回文串只与字符出现的奇偶性有关,我们把状态压一下
接下来我们套用淀粉质的思想,考虑用根来划分路径,然后合并根相连的两条路径,
怎么维护呢
我们发现对于这道题如果我们状态设计为\(f[x][S]\)表示以\(x\)为起点的到子树任意一点的状态为\(S\)最多的点数,
我们发现重儿子很不好向父亲传递信息,这样我们就无法套用dsu on tree 了,
但是我们想一下上几题查询子树中距离\(u\)为\(x\)的点的时候,
我们是怎么处理这个问题的,
我们把距离\(dis(x, u)\)改为了\(dis(ro,u) - dis(ro, x)\)
,我们发现了,貌似异或同样也具有做差的性质,然后就同样的处理,我们记录从根到\(x\)的这条路径的异或和,然后套用dsu on tree
天天爱跑步
一道很有挑战性的题目
首先我们思考暴力,那么每个点都搜一遍即可以处理问题
接着我们思考优化,首先本题显然不符合换根,
那么我们希望将问题统计转化为子树问题,这样就可以优秀时间复杂度
我们先进行思考,一个人什么时候会被观察员给看到
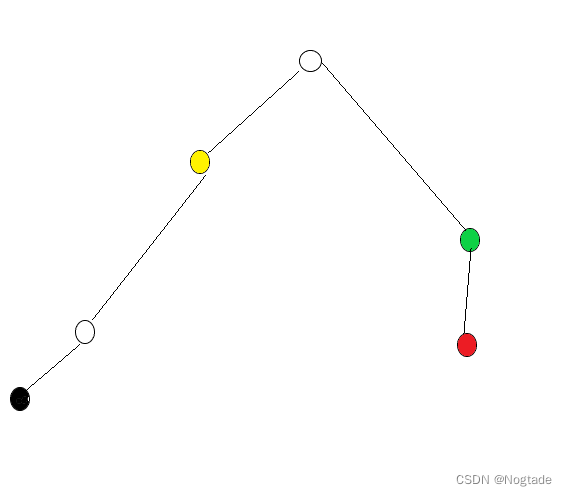
假设一个人\(p\)的初始点为黑色点\(u\),结束点为红色点\(v\),
那么我们发现在\(lca\)左侧的点,以黄色点\(x\)为例
如果\(x\)可以观察到\(p\), 那么需要满足
<1> \(dep[p] - dep[x] = w[x]\)
如果在\(lca\)右侧的店,以绿色点\(y\)为例
如果\(y\)可以观察到\(p\),那么需要满足
<2> \(dep[y] + dep[p] - 2*dep[lca]=w[y]\)
考虑将式子变得与\(x, y\)无关
则变形为
<1> \(dep[p] = w[x]+dep[x]\)
<2> \(dep[p]-2*dep[lca]=w[y]-dep[y]\)
这样我们对对每个点,查一查它的子树中有多少个<1>,有多少个<2>即可
但是要注意\(lca\)只需要加1次即可,树上差分一下
然后套上dsu on tree 优化复杂度
树上统计treecnt
我们观察这个式子,通常套路都为计算单边的出现次数然后累加
我们考虑一条边会被计算多少次
假设我们把数看成这条边\(T\)链接的两个连通块,那么如果\(L,R\)越过了\(T\)即可以被算上一次
如果我们计算只是单纯的\(siz[L]*siz[R]\)会发现少算
因为跨过\(T\)的\(L,R\)不一定非要分别位居两个连通块中
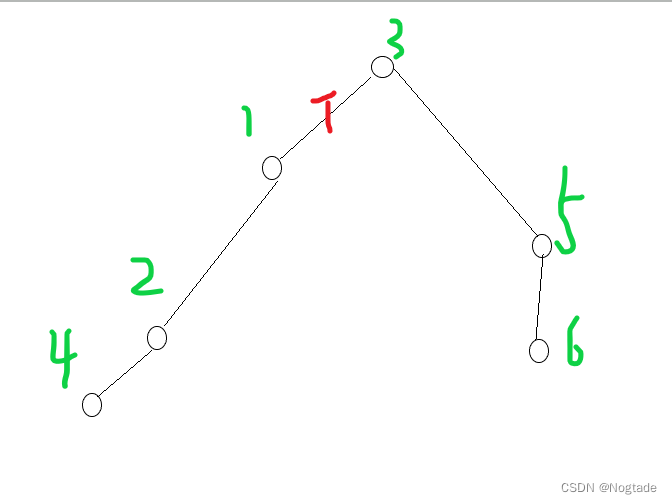
比如在这个例子中
\(siz[L]*siz[R]\)只是\((1,3),(1,5),(2,3),(2,5),(2,6),(4,3),(4,5),(4,6)\)
但是我们发现\((1,4),(3,5),(3,6)\)也会经过\(T\)
也就是说我们漏掉了一些情况
这样我们就很难统计了
不妨正难则反
我们用匹配的总数减去不用跨过\(T\)二元组的个数
我们统计\(T\)的\(L\)联通块,即\(1\)这颗子树,我们发现能够不经过\(T\)的二元组一定是连续的一段
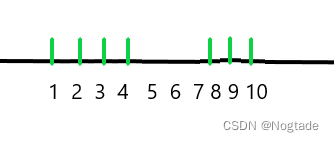
假设我们把\(1\)的子树中出现的点都打上标记如上图一样,那么\((1, 2),(1,3),(1,4),(2, 3),(3,4),(8,9),(8,10),(9,10)\)不需要经过
那么显然我们可以对于每个点加入的时候计算一下贡献,
同样对于子树外的点,则代表了这里面的\(0\)的段,但是我们发现不太好在加入的时候维护这个东西,
那么就维护一个\(set\)维护\(0\)段的区间,每次计算一下贡献,
然后套上dsu on tree 优化复杂度

