软工个人项目作业

一、项目地址

• 教学班级：006
• 项目地址：https://github.com/Knowden/intersectProject.git

二、开发时间

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划
Estimate	估计这个任务需要多少时间	5	5
Development	开发
Analysis	需求分析 (包括学习新技术)	90	120
Design Spec	生成设计文档	0
Design Review	设计复审 (和同事审核设计文档)	0
Coding Standard	代码规范 (为目前的开发制定合适的规范)	0
Design	具体设计	30	30
Coding	具体编码	150	300
Code Review	代码复审	15	60
Test	测试（自我测试，修改代码，提交修改）	60	80
Reporting	报告
Test Report	测试报告	60	30
Size Measurement	计算工作量	10	5
Postmortem & Process Improvement Plan	事后总结, 并提出过程改进计划	30	20
	合计	150	650

三、解题思路描述

浏览题目，首先明确输入输出格式、方式以及数据范围

第一想到的解法是数学法，对于两条直线，要么相交、要么平行（因为题目保证了不会重合），而对于圆和圆以及线和圆之间，交点可能的个数为0,1,2，可以通过解析式直接求出交点的具体坐标。

那么可以使用哈希集合，将每个点的x和y做哈希运算存储于哈希集合中，这样既保证了去重，也不会因去重而占用过多的计算时间。

这样的话，目前算法的时间复杂度在\(O(n^2)\)，对于性能测试时500000的数据量，这个时间复杂度肯定是跑不完的，所以开始考虑更优的解法。

经过思考，发现其他上面的分析中就暗藏了一个优化点，要么相交、要么平行，那么只有斜率不同的直线才会相交，所以计算的时候可以不进行斜率相同的直线间的计算，这样可以有效剪枝，在一定程度上提高算法的效率。

我尝试将算法的时间复杂度降阶，但是因为题目中允许多线共点，所以常规能找到的算法都统统不适用，毕竟若多线共点的话，不具体计算每个交点就无法判断是否是相同的点。

四、设计实现过程

整个的程序执行流程可以分为下面几步

• 读取输入，将每行输入转化为对应的对象存储于容器中
  • 若为直线（起首字符为L），则根据其斜率存储于map中
  • 若为圆圈（起首字符为C），则直接将其保存于一个vector中
• 计算直线间的交点，相同斜率（同一组）的不计算，将计算出的交点存于hashset
• 计算圆间的交点，存于hashset
• 计算直线和圆之间的交点，存于hashset
• 最终输出hashmap中元素的个数即为结果

这里借助hashmap来了保证点的唯一性

通过上面的流程分析，整个程序中共需要三个类，圆、直线、点

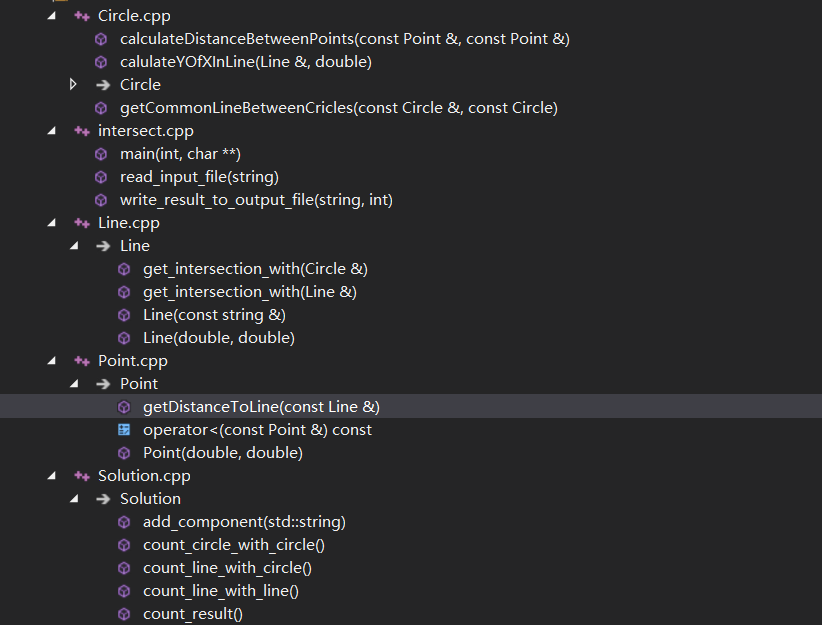
通过分析可以发现，其实圆和直线这两个类只要提供一个功能就可以了，就是计算自身与另外一个圆或直线的交点

所以在上面的图中可以看到，get_intersection_with函数在圆和直线类中都进行了重载操作，分别对应了圆类型和直线类型，这样可以在后续的操作中保持代码的简洁和一致。

特别的，我又专门将功能进行封装，提出了一个Solution类，这个类提供一个输入方法和一个输出方法，分别对应着每一行数据的加载和加载后统一计算结果值，最终main函数只需调用这个类即可，屏蔽了底层的复杂性，保证了代码逻辑的简洁。

关于单元测试在这里的地位是十分重要的，编写测试代码占用了整体编写代码时间的40%左右。

这次的问题虽然背景并不复杂，而且功能的需求也比较单一，但是边界情况意外的多，很多细节的地方需要处理，因此也需要分情况去进行测试，所以测试的工作还是比较繁重的。

我的单元测试是按类进行展开的，一个类做一套单元测试，这样完成对整个项目的单元测试编写。

首先是Point，这个类比较简单，主要的是用于统计输出结果和去重，因为之前对C++不太熟悉，所以专门对去重功能做了测试，保证这个类在Set中可以有效去重。

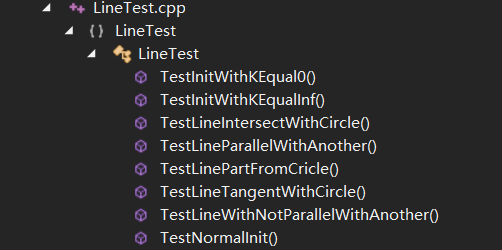
然后是Line的测试，主要包括线与线以及线与圆的相交测试，而线又包括有无斜率两种情况，线与线之间又包括平行和相交两种情况，线与圆之间又有相离、相切、相交三种情况，所以测试起来还是很多种情况的。

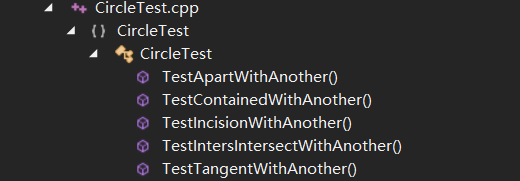
然后是Circle，因为线与圆的测试已经做好了，所以这里就只做了圆之间的测试，分别包括相离、相外切、相交、相内切、内含五种情况。

之后又补充了一些常规的顶层功能测试，确保各层可以正确的衔接配合工作，单元测试的编写工作就基本完成了。

测试的覆盖率还可以，没有覆盖到的基本上都是一些声明定义语句以及private函数，所有public的对外接口都进行了完整的测试。

五、代码度量

这里开启了最高的要求，没想到有这么多可以修改的地方

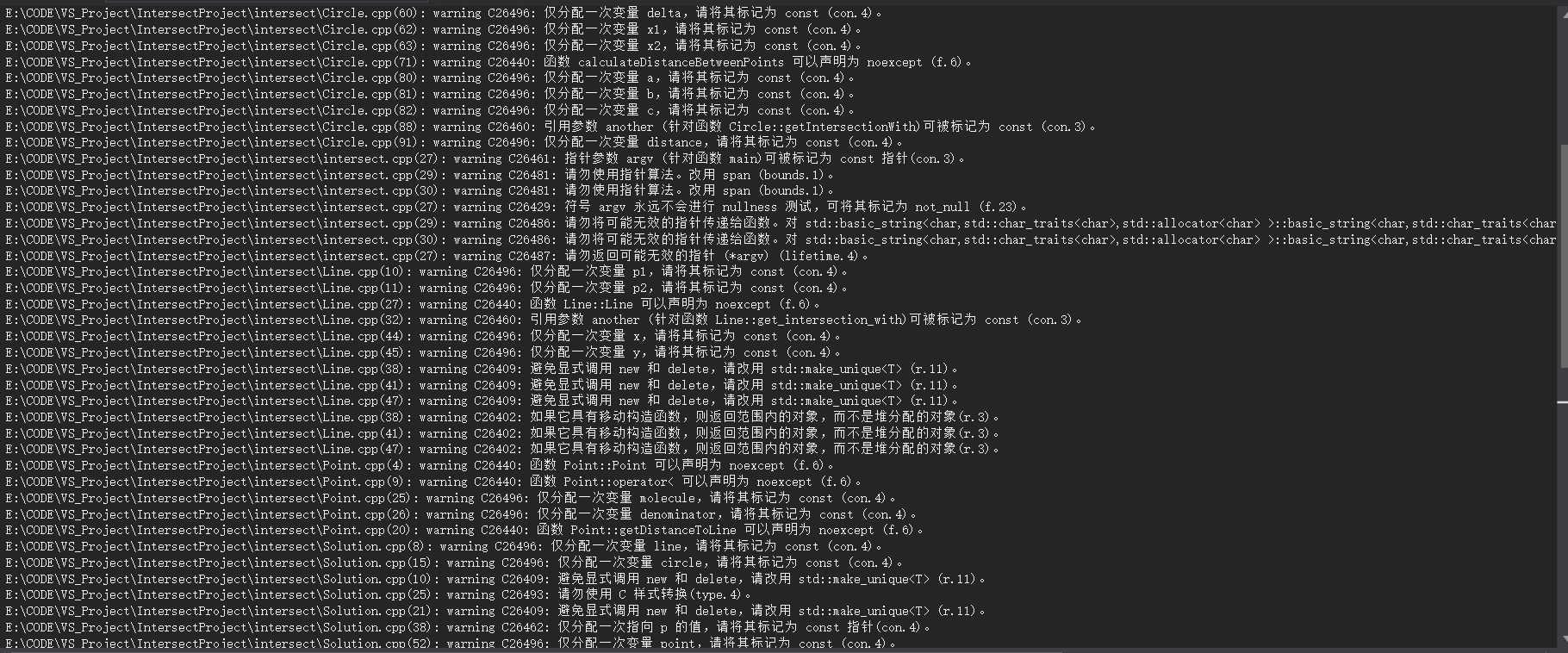
其中大多是要求一次赋值的变量用const声明，所以修改起来还是比较简单的

六、性能测试与优化

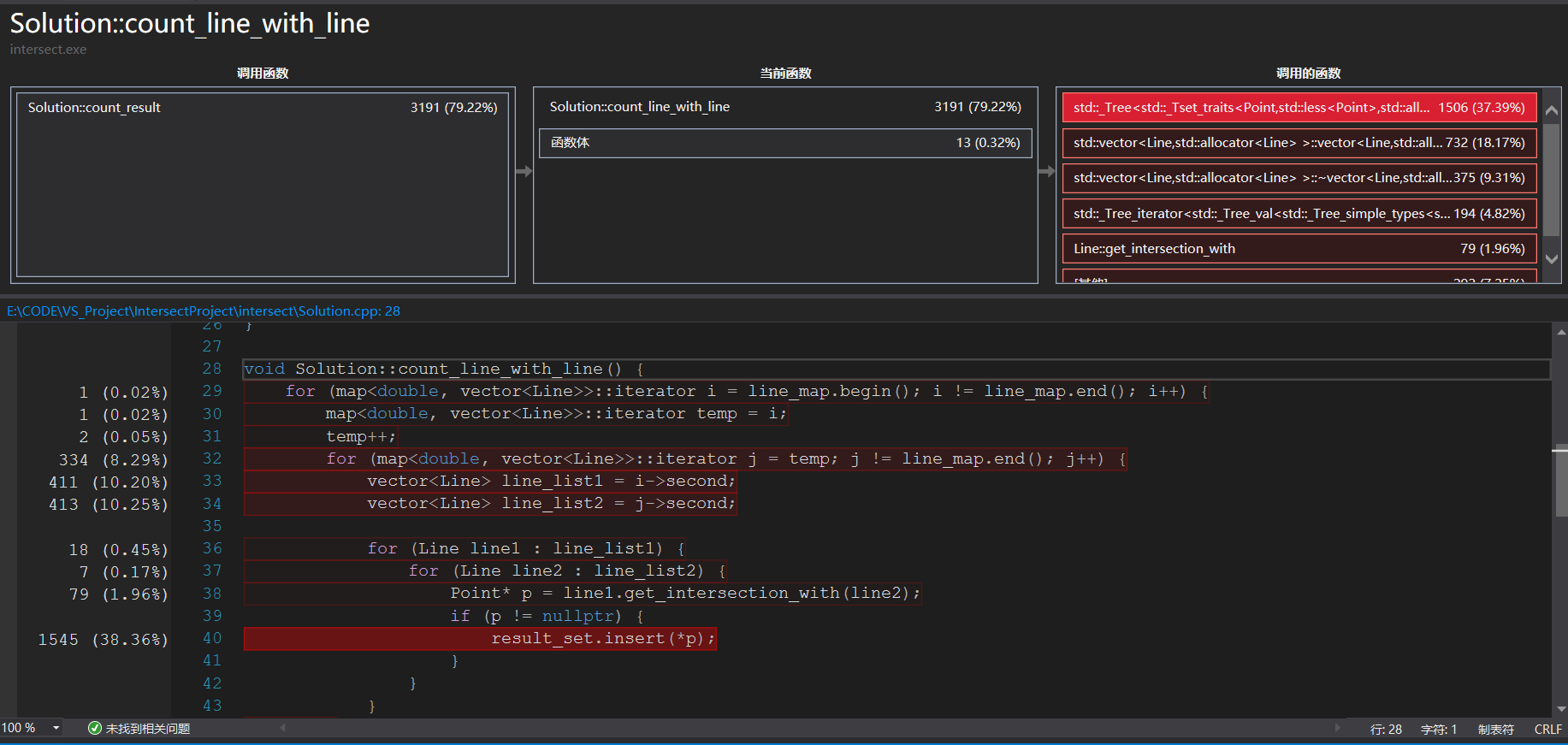
这里是使用了\(10^3\)数量级的数据，圆和线1:4生成数据进行测试的结果，count_line_with_line成为最耗时的函数我并不意外，意外的是其中set.insert操作占用了一半的时间而不是具体的交点计算等占用主要的时间，从图上也可以看到，真正的交点计算get_intersection_with只占用了2%不到的时间，看来C++中的set和我想象的hashset还是有所出入的，所以要考虑重点优化这个地方，也就是去重的策略。

经过查阅资料了解到，C++中的set是有序的，之所以需要重载比较运算符是因为它是基于比较排序来去重的，而unordered_set是利用hash进行去重的，所以这里改用unordered_set

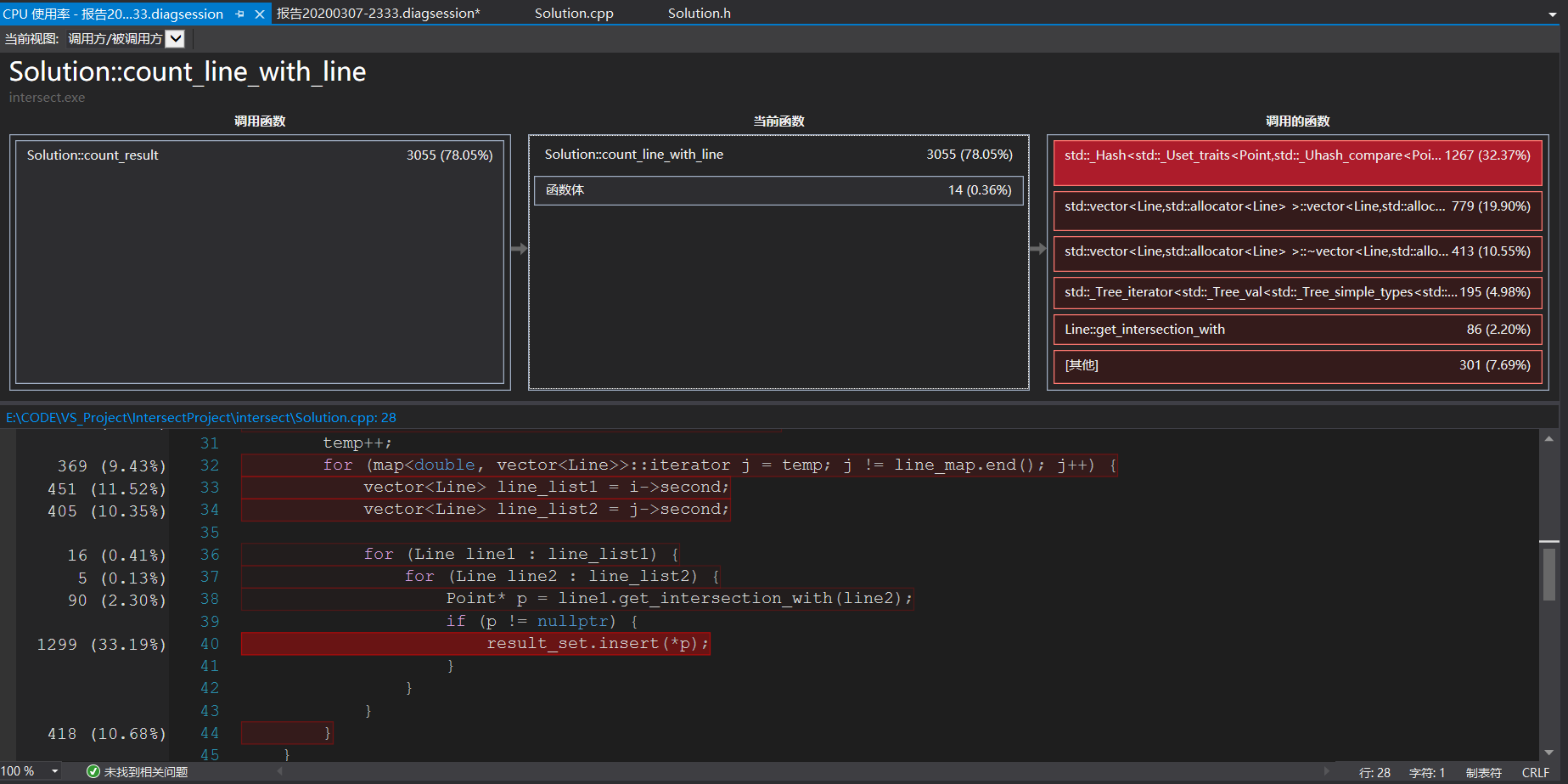
有所进步，但是并不是十分令人满意。

考虑到直接对Point.x和Point.y进行散列会使得单个set的散列空间变得十分大，所以下面考虑使用map<double, set<double>>的一个数据结构进行存储，看看效率能否提高。

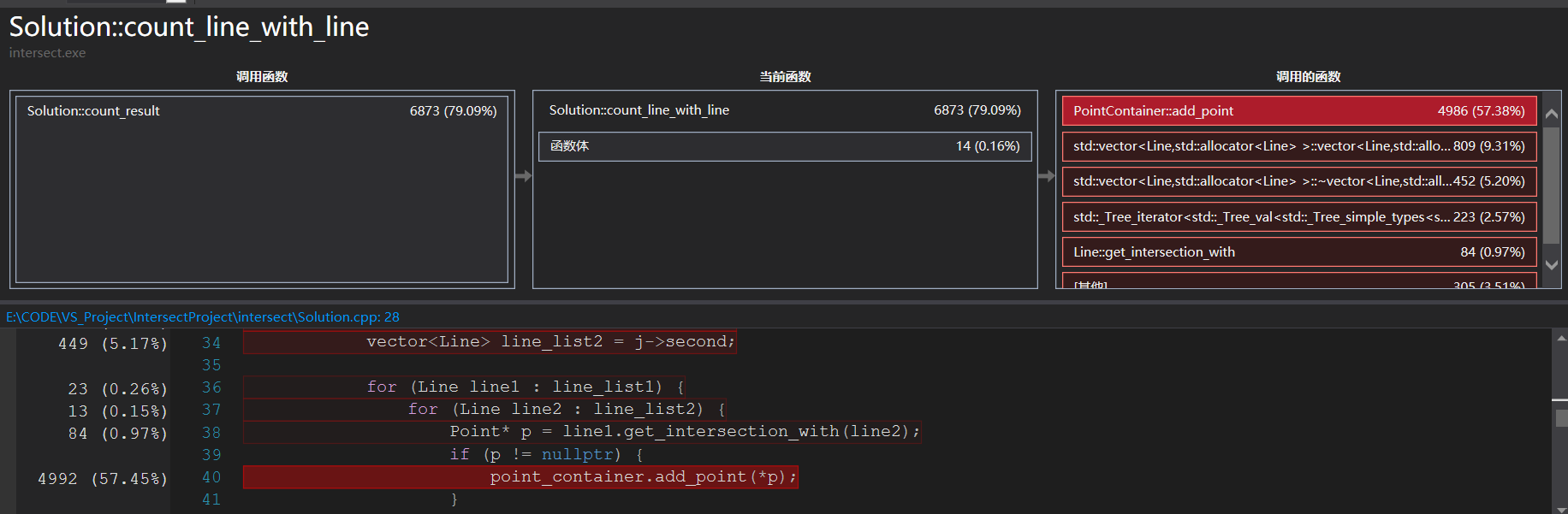
效果并不尽人意，看来虽然一次hash会导致整体的hash空间变大，但是毕竟只涉及一次hash寻址，而使用map<double, set>的结构会涉及两次hash，整体的时间代价反而更大，所以最终还是采用了第一次改进的方案。

之后，经过资料查询和学习，了解到stl中的set实现默认load_factor为1，所以会导致在resize之前会产生很多的冲突，而且因为本次项目中涉及的点的数量很大，所以set也会发生频繁的resize和rehash，这些都是十分占用计算资源的，所以针对这点我进行了优化和调整，最终使得set的时间占用下降到了27%左右，相比之前的32%又下降了5%。

七、代码说明

这次实现中最为麻烦的就是圆的处理，因为圆的解析式是二元二次的，所以计算起来很麻烦，情况也很多，容易出错。

同时，因为很多地方本质就是数学公式的计算步骤，所以写起来会比较面条，我尽可能减少了面条代码对核心逻辑的影响，使得主体代码的可读性维持在较好的水平。

vector<Point> Circle::getIntersectionWith(Line& line) {
    vector<Point> result;

    const double distance = this->center->getDistanceToLine(line);
    if (distance > this->r) {
        return result;
    }

    if (line.k == INT_MAX) {
        return calculatePointsAtX(line.b);
    }

    return calculateIntersectionWithNormalLine(line);
}

这里是关于圆和直线的代码，分为下面几个步骤

• 判断圆心和直线间的距离，若距离大于半径，则相离，直接返回空vector
• 若直线斜率不存在，这种情况下的计算方式和常规计算方式不同，只需把x坐标的值带入圆的解析式即可，所以单独创建了一个函数calculatePointsAtX
• 此外就是常规情况，即有交点且直线斜率存在，这种情况可以用一般的解析式带入求解，单独提取一个函数calculateIntersectionWithNormalLine

而上面提到的两个函数的内容就是解方程过程的模拟，就比较面条且没有可读性了，这方面怎么去进一步优化处理我还不太清楚，因为一个数学公式也没什么具体含义，所以我也没有办法再把计算过程拆分为几个步骤或者说有广泛意义的几个步骤，所以干脆没有进一步处理。

vector<Point> Circle::getIntersectionWith(Circle& another) {
    vector<Point> result;

    const double distance = calculateDistanceBetweenPoints(*center, *another.center);
    
    if (distance > r + another.r || distance < abs(r - another.r)) {
        return result;
    }

    Line common_line = getCommonLineBetweenCricles(*this, another);
    return getIntersectionWith(common_line);
}

然后是处理圆和圆的部分，这里的计算方式是借用两圆的共弦线来求出两个（或相同的两个）交点

• 先求出圆心距，若大于两元半径之和或小于两圆半径之差的绝对值，则没有交点，直接返回
• 否则有交点，则可求出共弦线common_line
• 圆和线的交点计算方法已经完成，直接调用自身的getIntersectionWith(Line)即可

这里的一个重点，也是我出过错误的地方是共弦线的计算，不能直接使用表达式计算，要特判一下共弦线斜率不存在的情况

Line getCommonLineBetweenCricles(const Circle& c1, const Circle c2) {
    if (c1.center->y == c2.center->y) {
        return Line(INT_MAX, ((pow(c1.r, 2) - pow(c2.r, 2)) / (c2.center->x - c1.center->x) + c1.center->x + c2.center->x) / 2);
    }

    const double a = 2 * (c2.center->x - c1.center->x);
    const double b = 2 * (c2.center->y - c1.center->y);
    const double c = (pow(c1.center->x, 2) + pow(c1.center->y, 2) - pow(c1.r, 2)) -
        (pow(c2.center->x, 2) + pow(c2.center->y, 2) - pow(c2.r, 2));

    return Line(-a / b, -c / b);
}

这里开始先判断了两圆心的纵坐标是否相等，若相等，则生成的共弦线斜率不存在，特殊处理。

其余的就比较好实现了，直线和直线间的可以直接用二元一次方程进行求解，特别注意斜率不存在的情况即可，而直线和圆的计算方法在圆中已经实现了（圆与直线的计算方法），直接调用圆对象的方法即可。

八、结语

这次的项目背景很简洁，要求也很明确，但是难度还是不小的，重点考察了开发人员的细心和测试规范。

个人做这次作业其实还是比较吃力的，因为C++语言很多特性用的不熟，踩了很多坑，VS也时不时地罢工一下（比如每次运行测试前必须点一下配置），说白了，还是菜（菜是原罪）。

不过虽然踩了很多坑，但是也从中吸取了很多经验和教训，进一步深入理解了C++的编译流程，.h文件和.cpp文件之间的配合，什么东西应该写在哪里，怎么写才是最优的工程实践等等。同时也接触到了很多开发软件的工具，或者说是一类方法，例如性能测试、代码度量等。以前做开发是没有用过性能测试的，也是因为自己本身不太注重这个，不出问题就不太在意性能，其实应该像对待单元测试一样对待性能测试，因为很多时候，如果项目的规模大了，到了最后项目冲刺的阶段又发现了性能问题，再把以前的基础代码刨出来修理一番，代价就太大了。