纽康悖论谜题

题目：有两个箱子，箱子A固定有1万元，箱子B可能有100万，也可能没有钱，而你可以选择单独拿走箱子B或者同时拿走两个箱子。有个预言准确率高达90%的巫师，在他预言你会单独拿走箱子B的时候，预先把100万放进箱子B中。请问，你会做哪种选择？

 

解题：

一般而言，如果巫师预言你不是只拿了箱子B，那么箱子B就是空的，这个时候你应该选择两个都拿，至少你能赚1万块。

如果巫师预言你只拿了箱子B，那么箱子B有100万，这个时候你也应该两个都拿，因为箱子A不管如何都是固定有一万块的，没理由眼巴巴看着箱子A的1万块不拿。

因此不管巫师的预言是什么，你都应该两个都拿。

另一个看法：

因为预言的准确率高达90%，也就是当你单独拿B的时候，90%的机率都是能拿到100万的，所以应该单独拿箱子B。如果你拿两个，只有10%的机会能拿到101万。选择单独拿箱子B不是理所当然的么？

 

这两种观点，不管单独从哪个看，都似乎无懈可击，但是结论却截然相反，这正是纽康悖论的精妙之处。

 

我的分析：

第一点：巫师不关心你赚了多少钱，他只关心预言命中的机率。而你的核心问题是如何赚最多的钱。所以两个问题的核心其实是不相冲突的。

第二点：机率是多次选择的结果。我想这就是问题的核心所在。如果是你自身做的多次选择，而不是多个人做的多次选择，你就能够控制最佳的结果。

当巫师对的时候，最佳结果是100万，当巫师错的时候最佳结果是101万。如果刚好9次对的100万，1次错的101万，那么有100×9+101=900+101=1001万的期望值。不过这是最佳的结果，坏的情况是8次对的100万，1次对的1万，1次错的0元，等于100×8+1+0 = 801万。1001万和801万究竟会出现哪一种情况，或者哪一种情况会占优？事实上这两种情况都是正确的组合，并没有哪个特别会占优，也就是（1001+801）/2= 901。这个是这种情况下一般期望值。如果10次都是选择只拿箱子B，那么结果是9次对的100万，1次错的0元，结果是900万的期望值。只要不断的计算下去，总能找到一个理想的方案。

不过以上分析都是基于自身做的选择的前提，也就是对几率做了人为的控制，这个前提也许根本就不存在。既然几率一般而言被认为真正随机的，客观的，不可控制的，那么实际上你做什么选择并不会影响几率。

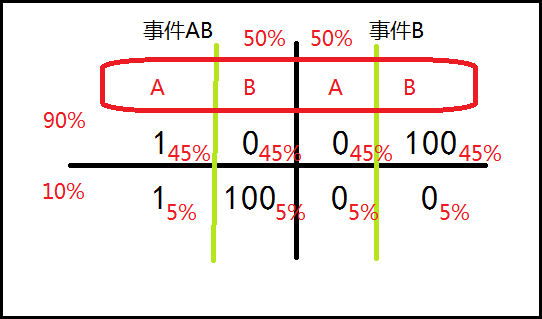
当选择AB的时候，结果有1万或者101万。当选择B的时候，结果有100万和0万。因为选择AB和选择B是相互独立的两个事件，各自都有50%的正确几率（事实上选择其中任意一个事件，都会降低另一个事件的几率，但是并没有任何条件表明那个事件选择的几率更高）。事件AB本身，1万的几率是100%，B盒100万的几率是10%，也就是1+10=11万。从整体来看，选择AB事件1万的几率是50%，100万的几率是5%，也就是0.5+5=5.5万。

事件B本身，100万的几率90%，0万的几率是10%，也就是90+0 = 90万。从整体来看，选择B事件，100万的几率是45%，0万的几率是5%，结果是45+0=45万。

因此，选择事件B，也就是只选择盒子B是合理的。