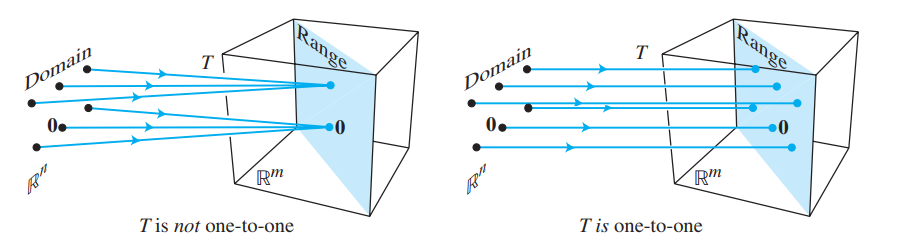
满射(onto) 和 单射(one-to-one)
-
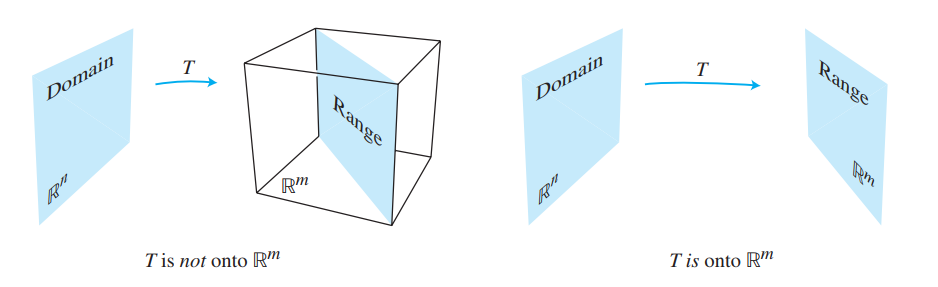
满射
A mapping \(T: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}\) is said to be onto \(\mathbb{R}^{m}\) if each \(\mathbf{b}\) in \(\mathbb{R}^{m}\) is the image of at least one \(\mathbf{x}\) in \(\mathbb{R}^{n}\).
-
单射
A mapping \(T: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}\) is said to be one-to-one if each \(\mathbf{b}\) in \(\mathbb{R}^{m}\) is the image of at most one \(\mathbf{x}\) in \(\mathbb{R}^{n}\).