linear transformation
-
Ax=b,Au=0 represent the transformation between x and b,0
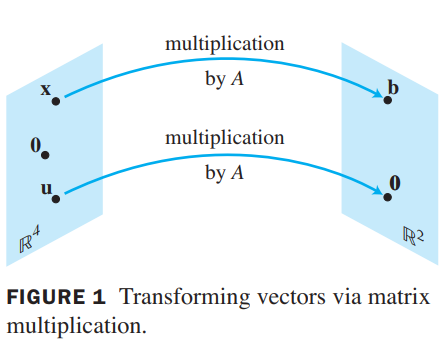
-
define a note T as the linear transformation, we call above as the linear transformation,for example T(x)=b,T(x)=0
-
then we represen the matrix for linear transformation
Let \(T: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}\) be a linear transformation.If there exists a unique matrix \(A\) such that
\[T(\mathbf{x})=A \mathbf{x} \quad \text { for all } \mathbf{x} \text { in } \mathbb{R}^{n}
\]
to find A,we could choose a way such that finding \(\left[\begin{array}{lll} T\left(\mathbf{e}_{1}\right) & \cdots & T\left(\mathbf{e}_{n}\right) \end{array}\right]\) to make A as that. where \(\mathbf{e}_{j}\) is the \(j\) th column of the identity matrix in $\mathbb{R}^{n}. \(A\) is the \(m \times n\) matrix.



