A Geometric Description of Span
-
Span one vector to a line
Let \(\mathbf{v}\) be a nonzero vector in \(\mathbb{R}^{3} .\) Then \(\operatorname{Span}\{\mathbf{v}\}\) is the set of all scalar multiples of \(\mathbf{v}\), which is the set of points on the line in \(\mathbb{R}^{3}\) through \(\mathbf{v}\) and \(\mathbf{0},\) so it is a line
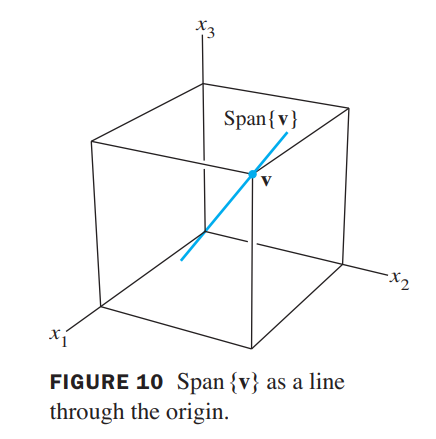
-
Span two vector to a plane
If \(\mathbf{u}\) and \(\mathbf{v}\) are nonzero vectors in \(\mathbb{R}^{3}\), with \(\mathbf{v}\) not a multiple of \(\mathbf{u}\), then \(\operatorname{Span}\{\mathbf{u}, \mathbf{v}\}\) is the plane in \(\mathbb{R}^{3}\) that contains \(\mathbf{u}, \mathbf{v}\), and \(\mathbf{0}\). In particular, \(\operatorname{Span}\{\mathbf{u}, \mathbf{v}\}\) contains the line in \(\mathbb{R}^{3}\) through \(\mathbf{u}\) and \(\mathbf{0}\) and the line through \(\mathbf{v}\) and \(\mathbf{0},\) so it is a plane
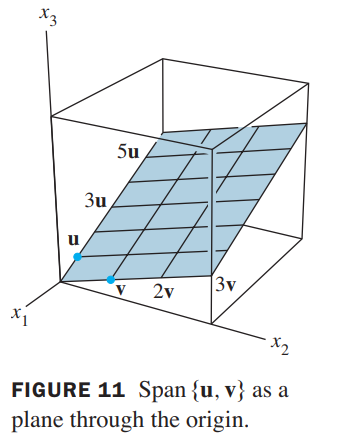
- How to Span \(\mathbb{R}^m\)
"The columns of \(A\) span \(\mathbb{R}^{m}\)", means that every \(\mathbf{b}\) in \(\mathbb{R}^{m}\) is a linear combination of the columns of \(A .\) that means that \(Ax=b\) is consistent,at least one solution. if \(A=\left\{\mathbf{v}_{1}, \ldots, \mathbf{v}_{p}\right\}\)
In general, a set of vectors \(\left\{\mathbf{v}_{1}, \ldots, \mathbf{v}_{p}\right\}\) in \(\mathbb{R}^{m}\) spans (or generates) \(\mathbb{R}^{m}\) if every vector in \(\mathbb{R}^{m}\) is a linear combination of \(\mathbf{v}_{1}, \ldots, \mathbf{v}_{p}-\) that is, if \(\operatorname{Span}\left\{\mathbf{v}_{1}, \ldots, \mathbf{v}_{p}\right\}=\mathbb{R}^{m}\)
Span=extend



