西瓜书习题试答-第08章-集成学习

试答系列：“西瓜书”-周志华《机器学习》习题试答
系列目录
[第01章：绪论]
[第02章：模型评估与选择]
[第03章：线性模型]
[第04章：决策树]
[第05章：神经网络]
[第06章：支持向量机]
第07章：贝叶斯分类器
第08章：集成学习
第09章：聚类
第10章：降维与度量学习
第11章：特征选择与稀疏学习
第12章：计算学习理论(暂缺)
第13章：半监督学习
第14章：概率图模型
(后续章节更新中...)

目录

8.1 假设抛硬币正面为上的概率为p，反面朝上的概率为1-p。令H(n)代表抛n次硬币所得正面朝上的次数，则最多k次正面朝上的概率为

\[P(H(n)\leq k)=\sum_{i=0}^k {n \choose i}p^i(1-p)^{n-i}\tag{8.43} \]

对δ>0,k=(p-δ)n，有Hoeffding不等式

\[P(H(n)\leq (p-\delta n)\leq e^{-2\delta^2 n}\tag{8.44} \]

试推导出式(8.3).
证明：(8.3)表达了集成错误率，当不超过半数预测正确时，集成分类器预测错误，因此集成错误率为：

\[\begin{aligned} &P(H(n)\neq f(x))\\ =&P(H(T)\leq[T/2])\\ =&\sum_{k=0}^{[T/2]}{T\choose k}(1-\epsilon)^k\epsilon^{T-k} \end{aligned}\]

注意，上式中第一行中的H(x)是集成分类器预测函数，第二行的H(T)是题目中所述的硬币朝上次数的函数。与题目中的(8.43)、(8.44)式对比，进行变量代换：n=T，p=1-ε，k=[T/2]，那么δ=1-ε-[T/2]/T。其中[T/2]/T≤1/2,所以δ≥1/2-ε，于是有

\[\begin{aligned} P(H(n)\neq f(x))&\leq exp(-2\delta^2T)\\ &\leq exp(-\frac{1}{2}(1-2\epsilon)^2 T) \end{aligned}\]

得证。

8.2 对于0/1损失函数来说，指数损失函数并非仅有的一致替代函数。考虑式(8.5)，试证明：任意损失函数 \(L(-f(x)H(x))\)，若对于H(x)在区间[-∞,δ] (δ>0)上单调递减，则是0/1损失函数的一致替代函数。

证明：这道题表述大概存在笔误，应该是“…，若对于f(x)H(x)在区间…”才对。比如，对于Adaboost中采用的指数损失函数，\(L(-f(x)H(x))=exp(-f(x)H(x))\)，当f(x)=1时，损失函数=exp(-H(x))是对于H(x)在[-∞，+∞]上的单调减函数，但是当f(x)=-1时，损失函数=exp(H(x))是H(x)的增函数，与题目描述不符。
对于任意损失函数，若对于f(x)H(x)在区间[-∞,δ] (δ>0)上单调递减，函数曲线当形如下图：
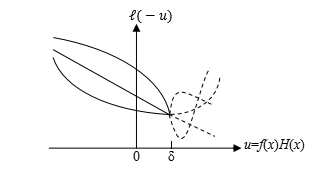
在这里插入图片描述
\(L(-u)\)函数的特点是：在[-∞,δ]区间是单调递减函数(无论其凹凸性如何)，在[δ,+∞]区间，可以是任意形状曲线，无论其单调性如何。从上图中可以看出，对该损失函数进行最小化时，所对应的横坐标位置u*总是在δ右侧，也就是f(x*)H(x*)≥δ>0，这说明H(x)与f(x)同正负号。因此sign(H(x*))=f(x*)，其结果与最小化0/1损失函数结果一致，是一致替代函数。

8.3 从网上下载或自己编程实现AdaBoost，以不剪枝决策树为基学习器，在西瓜数据集3.0α上训练一个AdaBoost集成，并与图8.4进行比较。

答：

1. AdaBoost算法总结

  • 西瓜书中的推导大概过程

\(\alpha_t=argmin_\alpha l_{exp}(\alpha_t h_t| D_t)=\frac{1}{2}\ln(\frac{1-\epsilon_t}{\epsilon_t})\)，其中\(\epsilon_t=P_{x\sim D_t}(f(x)\neq h_t(x))\)；
\(h_t (x)=argmin_h l_{exp}(H_{t-1}+h|D)\dots=argmin_h E_{x\sim D_t}[Ⅱ(f(x)\neq h(x))]\)，其中将\(H_{t-1}\)的影响包含在\(D_t\)中，\(D_t(x)\)是关于x的分布，\(D_t(x)∝D(x)e^{-f(x)H_{t-1}(x)}\)，Dt存在递推关系\(D_{t+1}=D_t e^{-f(x)\alpha_t h_t(x)}/Z_t\)。

然而，看完教材上的上述推导，心里充满了疑问：

  1. 为什么求\(α_t\)是通过最小化\(l_{exp}(α_th_t|D_t)\)来求得？
  2. 为什么通过最小化\(l_{exp}(H_{t-1}+h_t|D)\)来求取\(h_t\)时，\(h_t\)前面没有系数\(α_t\)，后面推导\(D_{t+1}\)和\(D_t\)的递推关系时，怎么就突然要加上系数\(α_t\)了？
  • 其他推导方法
    此前看过吴恩达的CS229课程，其补充材料中有介绍Boosting算法的内容，同样是对AdaBoost算法的推导，容易理解的多，现将其总结至此：
    (为了与西瓜书中的表达符号一致，对原文进行了一定的改写)

在计算到第t步时，当前已经得到的模型为\(H_{t-1}\)，接下来的学习器对当前模型\(H_{t-1}\)预测错误的样本进行重点关注，定义新的样本权重分布：

\[D_t(x)=D(x)e^{-f(x)H_{t-1}(x)}/E_{x\sim D}[e^{-f(x)H_{t-1}(x)}] \]

该权重分布反映了对预测错误样本的重点关注，因为，如果预测正确，\(e^{-f(x)H_{t-1}(x)}<1\),如果预测错误，\(e^{-f(x)H_{t-1}(x)}>1\)。
\(h_t(x)\)的确定：在新的样本权重下进行学习训练。
\(α_t\)的确定：

\[\begin{aligned} \alpha_t &=argmin_{\alpha}l_{exp}(H_t |D)\\ &=argmin_{\alpha}E_{x\sim D}[e^{-f(x)H_{t-1}(x)}\cdot e^{-f(x)\alpha_t h_t(x)}]\\ &=argmin_{\alpha}E_{x\sim D_t}[e^{-f(x)\alpha_t h_t(x)}]\\ &=argmin_{\alpha}(1-\epsilon_t)e^{-\alpha_t}+\epsilon_t e^{\alpha_t}\\ &=\frac{1}{2}ln(\frac{1-\epsilon_t}{\epsilon_t}) \end{aligned}\]

接着证明了 算法的收敛性，注意到\(D_t\)的归一化系数\(Z_t=E_{x\sim D}[e^{-f(x)H_{t-1}(x)}]=l_{exp}(H_{t-1}|D)\)，因此有：

\[\begin{aligned} l_{exp}(H_t |D)&=E_{x\sim D}[e^{-f(x)H_{t-1}(x)}\cdot e^{-f(x)\alpha_t h_t(x)}]\\ &=E_{x\sim D}[Z_t \cdot D_t(x)\cdot e^{-f(x)\alpha_t h_t(x)}]\\ &=l_{exp}(H_{t-1} |D)\cdot E_{x\sim D_t}[e^{-f(x)\alpha_t h_t(x)}]\\ &=l_{exp}(H_{t-1} |D)\cdot 2\sqrt{\epsilon_t(1-\epsilon_t)} \end{aligned}\]

设每个弱分类器的误差满足\(\epsilon_t \leq \frac{1}{2}-\gamma\)，则有：

\[\begin{aligned} l_{exp}(H_t |D)&=l_{exp}(H_{t-1} |D)\cdot 2\sqrt{\epsilon_t(1-\epsilon_t)}\\ &\leq l_{exp}(H_{t-1} |D)\cdot \sqrt{1-4\gamma^2} \end{aligned}\]

因此有：

\[l_{exp}(H_t |D)\leq l_{exp}(H_0|D)(1-4\gamma^2)^{t/2}=(1-4\gamma^2)^{t/2} \]

其中\(l_{exp}(H_0|D)=Z_0 =1\)，经过有限步T以后，必然有\(l_{exp}(H_T|D)< \frac{1}{m}\)，此时所有样本都被正确分类，对应的最大步数\(T_{max}=-2\ln m/ln(1-4γ^2)≤\ln m/2γ^2\).
至于为什么\(l_{exp}(H_T|D)< \frac{1}{m}\)时，所有样本都正确分类？因为\(l_{exp}(H_T|D)\geq l_{1/0}(H_T|D)=\epsilon\)，当\(l_{exp}(H_T|D)< \frac{1}{m}\)时，\(\epsilon=\frac{误分数}{m}<\frac{1}{m}\)，误分样本数<1，意味着所有样本都被正确分类。

  • 讨论
    现在可以回头来解答前面存在的疑问了：
  1. 为什么求\(α_t\)是通过最小化\(l_{exp}(α_th_t|D_t)\)来求得？
    最小化\(l_{exp}(α_th_t|D_t)\)实际上等价于最小化\(l_{exp}(H_{t-1}+α_th_t|D)\)，而后者正是我们最终的优化目标，如此便好理解了。
  2. 为什么通过最小化\(l_{exp}(H_{t-1}+h_t|D)\)来求取\(h_t\)时，\(h_t\)前面没有系数\(α_t\)，后面推导\(D_{t+1}\)和\(D_t\)的递推关系时，怎么就突然要加上系数\(α_t\)了？
    西瓜书上最小化\(l_{exp}(H_{t-1}+h_t|D)\)来求取\(h_t\)不太好理解，\(D_t\)是化简前式过程中析出的一部分，是个析出量。而CS229课程中的证明过程则直观易于理解，\(D_t\)反映了当前步骤对之前预测错误的样本进行重点关注的权重重新分配，是个直接定义量.

    另外，注意到，在上述证明算法收敛性的过程中，假设每个弱分类器的预测错误率优于随机分类器：\(\epsilon_t \leq \frac{1}{2}-\gamma\)，从而得到的结论\(l_{exp}(H_t |D)\leq l_{exp}(H_{t-1} |D)\sqrt{1-4\gamma^2}\)，接着有后面算法必然收敛的结论。其实，如果分类器很差，\(\epsilon_t >\frac{1}{2}+\gamma\)，也可以得到相同的结果。再者，即便分类器\(h_t(x)\)的错误率比随机分类器还差:\(\epsilon_t >\frac{1}{2}\)，由此得到的\(α_t<0\)，那么\(α_t h_t(x)=|α_t|·[-h_t(x)]\)，这相当于自动将\(h_t(x)\)进行了翻转纠正。

    因此，教材中提到的\(\epsilon_t <\frac{1}{2}\)的限制，完全没必要，真正关键的在于 错误率要远离1/2，更靠近0或者1都可以。 假如某次迭代时\(\epsilon_t =\frac{1}{2}\)，则\(α_t=0\)，\(l_{exp}(H_t |D)=l_{exp}(H_{t-1} |D)\)，不会再产生新的学习器，损失函数不再变化，Boosting算法陷入停滞，无法再进行下去。

2. 编程计算

题目上说“以不剪枝决策树为基学习器”，没明白什么意思，好像有问题。AdaBoost的基学习器通常是弱学习器，而不剪枝决策树第一步便可实现零误差分类，对应的\(α_1=∞\)，下一步的分布\(D_2=0\)，算法无法再进行下去。既然要与图8.4进行比较，下面的解答采用与之相同的决策树桩作为基学习器。
详细编程代码附后。
说明一点，根据前面讨论，对于每个决策树桩，我统一约定左分支取值为1，右分支取值为-1，即便当前\(h_t(x)\)的效果较差，\(\epsilon_t>1/2\)，流程也会通过\(α_t<0\)的方式自动将其纠正过来。

3. 运行结果讨论

首先，尝试在生成决策树桩时，以信息增益最大化来确定划分属性和划分点，结果失败，过程中会导致\(ε_t=1/2\)，Boosting算法无法再进行下去。
于是，改用最小化误差来进行划分选择：\(min E_{x\sim D_t}[Ⅱ(f(x)\neq h_t(x))]\)。计算结果如下：
在这里插入图片描述
在t=7时即达到零错误率(此处的错误率是指总的预测函数\(H_t(x)\)在原数据集D上的错误率，注意与\(\epsilon_t\)区分)。
正如前面的分析(“其他推导方法”中对收敛性的证明)，\(l_{exp}≥l_{0/1}=错误率ε\)，\(l_{exp}\)是\(l_{0/1}\)的上界，当\(l_{exp}<1/m\)时，必有\(l_{0/1}<1/m\)，必有\(l_{0/1}=0\)。
在这里插入图片描述
上图中采用与教材8.4中相同的表示方法：红粗线和黑细线分别表示集成和基学习器的分类边界。这里得到的分类边界与教材8.4有所不同。

另外，根据前面的讨论，只要\(\epsilon_t\)不等于1/2，都能保证\(l_{exp}\)收敛并在有限步迭代后达到零错误率。因此，我尝试了用随机方法产生\(h_t(x)\)，按理说仍然能够保证算法收敛，某次实验结果如下：
在这里插入图片描述
在这里插入图片描述
正如预期，尽管每个\(h_t\)是随机产生的，却能够确保算法收敛，只不过收敛速度较慢。损失函数\(l_{exp}\)总是单调下降的，错误率在t=29归零之后尽管有反弹，但总能稳定归零。

那么，在Adaboost算法中，当\(\epsilon_t\)=1/2时，可以不必break，可以重新随机产生一个\(\epsilon_t\)≠1/2 的基学习器来避免程序早停。
再次尝试通过信息增益最大化来进行划分，但是引入一个机制：当\(\epsilon_t\)=1/2时，重新随机产生一个弱学习器。某次实验结果如下：
在这里插入图片描述

8.4 Gradient Boosting [Friedman,2001]是一种常用的Boosting算法，试析其与AdaBoost的异同。

答：

  1. Gradient Boosting算法简介
    算法描述如下图所示(参考原论文，以及这篇博文)
    在这里插入图片描述
    下面试将Gradient Boosting算法改写成与本教材一致的表达方式：

    算法：Gradient Boosting

    1. \(h_0(x)=argmin_\alpha E_{x\sim D}[L(f(x),\alpha)]\)
    2. for t=1,2,...,T do：
    3. \(\,\,\,\,\,\,\,\,\tilde{y_i}=-[\frac{\partial L(f(x_i),H(x_i))}{\partial H(x_i)}]_{H(x)=H_{t-1}(x)}, i=1\sim m\)
    4. \(\,\,\,\,\,\,\,\,h_t(x)=argmin_{\beta,h}E_{x\sim D}[(\tilde{y}-\beta h(x))^2]\)
    5. \(\,\,\,\,\,\,\,\,\alpha_t=argmin_\alpha E_{x\sim D}[L(y,H_{t-1}(x)+\alpha h_t(x))]\)
    6. \(\,\,\,\,\,\,\,\,H_t(x)=H_{t-1}(x)+\alpha_t h_t(x)\)
    7. end for

    讨论
    Gradient Boosting算法第3行即是求取目标函数L关于预测函数H的负梯度。比如，\(L=(y-H)^2\)，则有\(\partial L/\partial H=2(H-y)\)。
    此前，在对率回归和神经网络的训练中我们了解过梯度下降法，不过，那里是求取目标函数L关于参数θ的梯度。预测函数H(x;θ)的模型本身的形式不变，比如对率回归中，它固定是线性函数，在神经网络中，各层神经元数目固定，而参数θ则可任意变化。我们的任务是在θ的参数空间中搜索最佳参数。
    然而在这里，我们把H看成可以任意变化的函数，L是关于H这个函数的函数(泛函)。如果H真的可以任意变化，我们直接令H(x)=y不就好了。也有可能H(x)=y未必使L达到最小，此时可以通过最小化\(L(y,H_{t-1}+h)\)来求取\(h_t\)。
    然而，通常H不能任意变化，具体在boosting算法中，H被限定为多个弱学习器相加的形式。那么在第t步确定\(h_t\)时，Gradient Boosting算法便是以这个负梯度作为启发方向，使\(h_t\)应该尽可能地接近于该方向。
    Gradient Boosting算法适用于多种形式的损失函数。如果L取与AdaBoost中一样的指数损失函数，并且f(x)={1,-1}，我们可以试着推导一下，结果应如是：

    算法：exp-boost

    1. \(h_0(x)=sign(m_+-m_-)\)
    2. for t=1,2,...,T do：
    3. \(\,\,\,\,\,\,\,\,\tilde{y_i}=f(x_i)exp[-f(x_i)H_{t-1}(x_i)], i=1\sim m\)
    4. \(\,\,\,\,\,\,\,\,h_t(x)=argmin_{\beta,h}E_{x\sim D}[(\tilde{y}-\beta h(x))^2]=\cdots=argmin_hE_{x\sim D_t}[Ⅱ(f(x)\neq h(x))]\)
    5. \(\,\,\,\,\,\,\,\,\alpha_t=argmin_\alpha E_{x\sim D}[L(y,H_{t-1}(x)+\alpha h_t(x))]=\cdots=\frac{1}{2}ln\frac{1-\epsilon_t}{\epsilon_t}\)
    6. \(\,\,\,\,\,\,\,\,H_t(x)=H_{t-1}(x)+\alpha_t h_t(x)\)
    7. end for

    可见，此时Gradient Boosting算法除了多了一个\(h_0(x)\)，相应的初始分布D1有所不同，在t=1,2…,T迭代步骤中，\(h_t\)和\(\alpha_t\)的计算方法与AdaBoost算法完全相同。

  2. 比较Gradient Boosting和AdaBoost算法
    相同点：
    预测函数H(x)同样是“加性模型”，亦即基学习器的线性组合；
    第t步产生\(h_t\)和\(\alpha_t\)时，都保持前面的\(H_{t-1}(x)\)不变；
    \(\alpha_t\)的计算都是通过在既定\(h_t(x)\)的情况下来最小化目标函数；
    AdaBoost算法可以看成是在指数损失函数和y={1,-1}情况下的Gradient Boosting算法特例；
    不同点：
    求取\(h_t\)的思路不同(尽管在指数损失函数和y={1,-1}情况下结果一样)，在AdaBoost中，根据当前\(H_{t-1}(x)\)的预测效果来重新调整各个样本的权重，提高错误样本的权重，基于此来训练\(h_t(x)\)。而在Gradient Boosting中，通过寻找与负梯度方向最接近的函数\(h_t(x)=argmin_h|\nabla_HL-βh(x)|^2\)。
    Gradient Boosting算法适用范围更广，函数取值可以连续取值、离散取值(不限于y={1,-1})，损失函数可以是平方差，绝对偏差，Huber，logistic型。而AdaBoost算法只能用于二分类的情况。

8.5 试编程实现Bagging，以决策树桩为基学习器，在西瓜数据集3.0α上训练一个Bagging集成，并与图8.6进行比较。

答：详细编程代码附后。
以桩决策树为基学习器，下图是某一次的计算结果：
在这里插入图片描述
在这里插入图片描述
可见，训练误差最低为0.17，最少有3个样本被误分。与图8.6比较，分类效果较差，哪里出了问题？
网上查阅相关介绍，比如这篇博文。
了解到：Boosting算法的基学习器通常是弱学习器，特点是偏差较大，通过Boosting算法可以逐步提升，较低偏差；而Bagging的基学习器通常是强学习器，比如，全决策树和神经网络，特点是偏差较小，但是容易过拟合，方差较大，通过多个基学习器的平均来减小方差，防止过拟合。
这里采用的基学习器是决策树桩，本身偏差较大，Bagging集成只有降低方差的效果，对于偏差并无改善，所以集成后的训练误差仍然很低。于是，我们将基学习器改为全决策树，下图是某次计算结果：
在这里插入图片描述
在这里插入图片描述
可见，前4个集成后便已经实现了零训练误差。

8.6 试析Bagging通常为何难以提升朴素贝叶斯分类器的性能。

答：参考上题8.5的一些结论，朴素贝叶斯分类器本身的特点是偏差较大，算是弱学习

8.7 试析随机森林为何比决策树Bagging集成的训练速度更快。

答：在选择划分属性时，随机森林只需考察随机选取的几个属性，而决策树Bagging则要考察所有属性，因此训练速度更快。

8.8 MultiBoosting算法[Webb,2000]将AdaBoost作为Bagging的基学习器，Iterative Bagging算法[Breiman,2001b]则将Bagging作为AdaBoost的基学习器。试比较二者的优缺点。（暂缺）

答：

8.9 试设计一种可视的多样性度量，对习题8.3和习题8.5中得到的集成进行评估，并与κ-误差图比较。（暂缺）

答：

8.10 试设计一种能提升k近邻分类器性能的集成学习算法。（暂缺）

答：

附：习题代码

8.3(python)

# -*- coding: utf-8 -*-
"""
Created on Wed Mar 11 09:50:11 2020

@author: MS
"""

import numpy as np
import matplotlib.pyplot as plt

#设置出图显示中文
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False

def Adaboost(X,Y,T,rule='MaxInfoGain',show=False):
    # 以决策树桩为基学习器的Adaboost算法
    # 输入:
    #     X:特征，m×n维向量
    #     Y：标记,m×1维向量
    #     T：训练次数
    #     rule:决策树桩属性划分规则，可以是：
    #          'MaxInfoGain'，'MinError','Random'
    #     show:是否计算并显示迭代过程中的损失函数和错误率
    # 输出:
    #     H:学习结果，T×3维向量，每行对应一个基学习器，
    #       第一列表示αt,第二列表示决策树桩的分类特征，第三列表示划分点
    
    m,n=X.shape        #样本数和特征数
    D=np.ones(m)/m     #初始样本分布
    H=np.zeros([T,3])  #初始化学习结果为全零矩阵 
    #~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
    #这部分用于计算迭代过程中的损失函数和错误率的变化
    #可有可无
    H_pre=np.zeros(m)  #H对各个样本的预测结果
    L=[]               #存储每次迭代后的损失函数
    erro=[]            #存储每次迭代后的错误率
    #~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
    for t in range(T):
        if rule=='MaxInfoGain':
            ht=decision_sdumps_MaxInfoGain(X,Y,D)
        elif rule=='MinError':
            ht=decision_sdumps_MinError(X,Y,D)
        else:  #rule=='Random'或者其他未知取值时，随机产生
            ht=decision_sdumps_Random(X,Y,D)
        ht_pre=(X[:,ht[0]]<=ht[1])*2-1   #左分支为1，右分支为-1
        et=sum((ht_pre!=Y)*D)
        while abs(et-0.5)<1E-3:
            # 若et=1/2，重新随机生成
            ht=decision_sdumps_Random(X,Y,D)
            ht_pre=(X[:,ht[0]]<=ht[1])*2-1
            et=sum((ht_pre!=Y)*D)
        alphat=0.5*np.log((1-et)/et)
        H[t,:]=[alphat]+ht
        #~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
        #这部分用于计算迭代过程中的损失函数和错误率的变化
        #可有可无
        if show:
            H_pre+=alphat*ht_pre
            L.append(np.mean(np.exp(-Y*H_pre)))
            erro.append(np.mean(np.sign(H_pre)!=Y))
        #~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
        D*=np.exp(-alphat*Y*ht_pre)
        D=D/D.sum()
    #~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
    #这部分用于显示迭代过程中的损失函数和错误率的变化
    #可有可无
    if show:
        try:
            plt.title('t=%d时错误率归0'%(np.where(np.array(erro)==0)[0][0]+1))
        except:
            plt.title('错误率尚未达到0')
        plt.plot(range(1,len(L)+1),L,'o-',markersize=2,label='损失函数的变化')
        plt.plot(range(1,len(L)+1),erro,'o-',markersize=2,label='错误率的变化')
        plt.plot([1,len(L)+1],[1/m,1/m],'k',linewidth=1,label='1/m 线')
        plt.xlabel('基学习器个数')
        plt.ylabel('指数损失函数/错误率')
        plt.legend()
        plt.show()
    #~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
    return H

def decision_sdumps_MinError(X,Y,D):
    # 基学习器---决策树桩
    # 以最小化错误率来选择划分属性和划分点    
    m,n=X.shape        #样本数和特征数
    results=[]         #存储各个特征下的最佳划分点和错误率
    for i in range(n): #遍历各个候选特征
        x=X[:,i]               #样本在该特征下的取值
        x_sorted=np.unique(x)  #该特征下的可能取值并排序
        ts=(x_sorted[1:]+x_sorted[:-1])/2   #候选划分点
        Errors=[]              #存储各个划分点下的|错误率-0.5|的值
        for t in ts:
            Ypre=(x<=t)*2-1
            Errors.append(abs(sum(D[Ypre!=Y])-0.5))
        Bestindex=np.argmax(Errors)   #距离0.5最远的错误率的索引号
        results.append([ts[Bestindex],Errors[Bestindex]])
    
    results=np.array(results)
    divide_feature=np.argmax(results[:,1])         #划分特征
    h=[divide_feature,results[divide_feature,0]]   #划分特征和划分点
    return h

def decision_sdumps_MaxInfoGain(X,Y,D):
    # 基学习器---决策树桩
    # 以信息增益最大来选择划分属性和划分点    
    m,n=X.shape        #样本数和特征数
    results=[]         #存储各个特征下的最佳划分点和信息增益
    for i in range(n): #遍历各个候选特征
        x=X[:,i]               #样本在该特征下的取值
        x_sorted=np.unique(x)  #该特征下的可能取值并排序
        ts=(x_sorted[1:]+x_sorted[:-1])/2   #候选划分点
        Gains=[]               #存储各个划分点下的信息增益
        for t in ts:
            Gain=0
            Y_left,D_left=Y[x<=t],D[x<=t]    #左分支样本的标记和分布
            Dl=sum(D_left)                   #左分支总分布数
            p1=sum(D_left[Y_left==1])/Dl     #左分支正样本分布比例
            p0=sum(D_left[Y_left==-1])/Dl    #左分支负样本分布比例
            Gain+=Dl*(np.log2(p1**p1)+np.log2(p0**p0))
            
            Y_right,D_right=Y[x>t],D[x>t]    #右分支样本的标记和分布
            Dr=sum(D_right)                  #右分支总分布数
            p1=sum(D_right[Y_right==1])/Dr   #右分支正样本分布比例
            p0=sum(D_right[Y_right==-1])/Dr  #右分支负样本分布比例
            Gain+=Dr*(np.log2(p1**p1)+np.log2(p0**p0))
            
            Gains.append(Gain)
            
        results.append([ts[np.argmax(Gains)],max(Gains)])
    
    results=np.array(results)
    divide_feature=np.argmax(results[:,1])               #划分特征
    h=[divide_feature,results[divide_feature,0]]         #划分特征和划分点
    return h

def decision_sdumps_Random(X,Y,D):
    # 基学习器---决策树桩
    # 随机选择划分属性和划分点    
    m,n=X.shape          #样本数和特征数
    bestfeature=np.random.randint(2)
    x=X[:,bestfeature]   #样本在该特征下的取值
    x_sorted=np.sort(x)  #特征取值排序
    ts=(x_sorted[1:]+x_sorted[:-1])/2   #候选划分点
    bestt=ts[np.random.randint(len(ts))]
    h=[bestfeature,bestt]
    return h

def predict(H,X1,X2):
    # 预测结果
    # 仅X1和X2两个特征,X1和X2同维度
    pre=np.zeros(X1.shape)
    for h in H:
        alpha,feature,point=h
        pre+=alpha*(((X1*(feature==0)+X2*(feature==1))<=point)*2-1)
    return np.sign(pre)

##############################
#      主程序
##############################
#>>>>>西瓜数据集3.0α
X=np.array([[0.697,0.46],[0.774,0.376],[0.634,0.264],[0.608,0.318],[0.556,0.215],
   [0.403,0.237],[0.481,0.149],[0.437,0.211],[0.666,0.091],[0.243,0.267],
   [0.245,0.057],[0.343,0.099],[0.639,0.161],[0.657,0.198],[0.36,0.37],
   [0.593,0.042],[0.719,0.103]])
Y=np.array([1,1,1,1,1,1,1,1,-1,-1,-1,-1,-1,-1,-1,-1,-1])

#>>>>>运行Adaboost
T=50
H=Adaboost(X,Y,T,rule='MaxInfoGain',show=True)
# rule:决策树桩属性划分规则，可以取值：'MaxInfoGain'，'MinError','Random'

#>>>>>观察结果
x1min,x1max=X[:,0].min(),X[:,0].max()
x2min,x2max=X[:,1].min(),X[:,1].max()
x1=np.linspace(x1min-(x1max-x1min)*0.2,x1max+(x1max-x1min)*0.2,100)
x2=np.linspace(x2min-(x2max-x2min)*0.2,x2max+(x2max-x2min)*0.2,100)
X1,X2=np.meshgrid(x1,x2)

for t in [3,5,11,30,40,50]:
    plt.title('前%d个基学习器'%t)
    plt.xlabel('密度')
    plt.ylabel('含糖量')
    # 画样本数据点
    plt.scatter(X[Y==1,0],X[Y==1,1],marker='+',c='r',s=100,label='好瓜')
    plt.scatter(X[Y==-1,0],X[Y==-1,1],marker='_',c='k',s=100,label='坏瓜')
    plt.legend()
    # 画基学习器划分边界
    for i in range(t):
        feature,point=H[i,1:]
        if feature==0:
            plt.plot([point,point],[x2min,x2max],'k',linewidth=1)
        else:
            plt.plot([x1min,x1max],[point,point],'k',linewidth=1)
    # 画集成学习器划分边界
    Ypre=predict(H[:t],X1,X2)
    plt.contour(X1,X2,Ypre,colors='r',linewidths=5,levels=[0])
    plt.show()

8.5(python)

以决策树桩为基学习器

# -*- coding: utf-8 -*-
"""
Created on Wed Mar 11 09:50:11 2020

@author: MS
"""

import numpy as np
import matplotlib.pyplot as plt

#设置出图显示中文
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False

def decision_sdumps_MaxInfoGain(X,Y):
    # 基学习器---决策树桩
    # 以信息增益最大来选择划分属性和划分点    
    m,n=X.shape        #样本数和特征数
    results=[]         #存储各个特征下的最佳划分点,左分支取值，右分支取值，信息增益
    for i in range(n): #遍历各个候选特征
        x=X[:,i]                 #样本在该特征下的取值
        x_values=np.unique(x)    #当前特征的所有取值
        ts=(x_values[1:]+x_values[:-1])/2   #候选划分点
        Gains=[]             #存储各个划分点下的信息增益
        for t in ts:
            Gain=0
            Y_left=Y[x<=t]           #左分支样本的标记
            Dl=len(Y_left)           #左分支样本数
            p1=sum(Y_left==1)/Dl     #左分支正样本比例
            p0=sum(Y_left==-1)/Dl    #左分支负样本比例
            Gain+=Dl/m*(np.log2(p1**p1)+np.log2(p0**p0))
            
            Y_right=Y[x>t]          #右分支样本的标记
            Dr=len(Y_right)         #右分支总样本数
            p1=sum(Y_right==1)/Dr   #右分支正样本比例
            p0=sum(Y_right==-1)/Dr  #右分支负样本比例
            Gain+=Dr/m*(np.log2(p1**p1)+np.log2(p0**p0))
            
            Gains.append(Gain)
        best_t=ts[np.argmax(Gains)]  #当前特征下的最佳划分点
        best_gain=max(Gains)         #当前特征下的最佳信息增益
        left_value=(sum(Y[x<=best_t])>=0)*2-1   #左分支取值(多数类的类别)
        right_value=(sum(Y[x>best_t])>=0)*2-1   #右分支取值(多数类的类别)
        results.append([best_t,left_value,right_value,best_gain])
    
    results=np.array(results)
    df=np.argmax(results[:,-1])       #df表示divide_feature，划分特征
    h=[df]+list(results[df,:3])       #划分特征,划分点,左枝取值，右枝取值
    return h

def predict(H,X1,X2):
    # 预测结果
    # 仅X1和X2两个特征,X1和X2同维度
    pre=np.zeros(X1.shape)
    for h in H:
        df,t,lv,rv=h  #划分特征,划分点,左枝取值，右枝取值
        X=X1 if df==0 else X2
        pre+=(X<=t)*lv+(X>t)*rv
    return np.sign(pre)



#>>>>>西瓜数据集3.0α
X=np.array([[0.697,0.46],[0.774,0.376],[0.634,0.264],[0.608,0.318],[0.556,0.215],
   [0.403,0.237],[0.481,0.149],[0.437,0.211],[0.666,0.091],[0.243,0.267],
   [0.245,0.057],[0.343,0.099],[0.639,0.161],[0.657,0.198],[0.36,0.37],
   [0.593,0.042],[0.719,0.103]])
Y=np.array([1,1,1,1,1,1,1,1,-1,-1,-1,-1,-1,-1,-1,-1,-1])
m=len(Y)
#>>>>>Bagging
T=20
H=[]       #存储各个决策树桩，
           #每行为四元素列表，分别表示划分特征,划分点,左枝取值，右枝取值
H_pre=np.zeros(m)  #存储每次迭代后H对于训练集的预测结果
error=[]           #存储每次迭代后H的训练误差
for t in range(T):
    boot_strap_sampling=np.random.randint(0,m,m)   #产生m个随机数
    Xbs=X[boot_strap_sampling]                     #自助采样
    Ybs=Y[boot_strap_sampling]                     #自助采样
    h=decision_sdumps_MaxInfoGain(Xbs,Ybs)         #训练基学习器
    H.append(h)                                    #存入基学习器
    #计算并存储训练误差
    df,t,lv,rv=h                                   #基学习器参数
    Y_pre_h=(X[:,df]<=t)*lv+(X[:,df]>t)*rv         #基学习器预测结果
    H_pre+=Y_pre_h                                 #更新集成预测结果
    error.append(sum(((H_pre>=0)*2-1)!=Y)/m)       #当前集成预测的训练误差
H=np.array(H)

#>>>>>绘制训练误差变化曲线
plt.title('训练误差的变化')
plt.plot(range(1,T+1),error,'o-',markersize=2)
plt.xlabel('基学习器个数')
plt.ylabel('错误率')
plt.show()
#>>>>>观察结果
x1min,x1max=X[:,0].min(),X[:,0].max()
x2min,x2max=X[:,1].min(),X[:,1].max()
x1=np.linspace(x1min-(x1max-x1min)*0.2,x1max+(x1max-x1min)*0.2,100)
x2=np.linspace(x2min-(x2max-x2min)*0.2,x2max+(x2max-x2min)*0.2,100)
X1,X2=np.meshgrid(x1,x2)

for t in [3,5,11,15,20]:
    plt.title('前%d个基学习器'%t)
    plt.xlabel('密度')
    plt.ylabel('含糖量')
    #plt.contourf(X1,X2,Ypre)
    # 画样本数据点
    plt.scatter(X[Y==1,0],X[Y==1,1],marker='+',c='r',s=100,label='好瓜')
    plt.scatter(X[Y==-1,0],X[Y==-1,1],marker='_',c='k',s=100,label='坏瓜')
    plt.legend()
    # 画基学习器划分边界
    for i in range(t):
        feature,point=H[i,:2]
        if feature==0:
            plt.plot([point,point],[x2min,x2max],'k',linewidth=1)
        else:
            plt.plot([x1min,x1max],[point,point],'k',linewidth=1)
    # 画基集成效果的划分边界
    Ypre=predict(H[:t],X1,X2)
    plt.contour(X1,X2,Ypre,colors='r',linewidths=5,levels=[0])   
    plt.show()

以完整决策树作为基学习器

# -*- coding: utf-8 -*-
"""
Created on Tue Mar 17 13:16:42 2020

@author: MS

前面采用决策树桩来进行Bagging集成，效果较差，
现在改用全决策树full-tree来集成，观察效果。
全决策树算法不再自编，直接采用sklearn工具。
"""


import numpy as np
import matplotlib.pyplot as plt
from sklearn import tree

#设置出图显示中文
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False

def predict(H,X1,X2):
    # 预测结果
    # 仅X1和X2两个特征,X1和X2同维度
    X=np.c_[X1.reshape(-1,1),X2.reshape(-1,1)]
    Y_pre=np.zeros(len(X))
    for h in H:
        Y_pre+=h.predict(X)
    Y_pre=2*(Y_pre>=0)-1
    Y_pre=Y_pre.reshape(X1.shape)
    return Y_pre



#>>>>>西瓜数据集3.0α
X=np.array([[0.697,0.46],[0.774,0.376],[0.634,0.264],[0.608,0.318],[0.556,0.215],
   [0.403,0.237],[0.481,0.149],[0.437,0.211],[0.666,0.091],[0.243,0.267],
   [0.245,0.057],[0.343,0.099],[0.639,0.161],[0.657,0.198],[0.36,0.37],
   [0.593,0.042],[0.719,0.103]])
Y=np.array([1,1,1,1,1,1,1,1,-1,-1,-1,-1,-1,-1,-1,-1,-1])

#>>>>>Bagging
T=20
H=[]       #存储各个决策树桩，每行表示#划分特征,划分点,左枝取值，右枝取值
m=len(Y)
H_pre=np.zeros(m)  #存储每次迭代后H对于训练集的预测结果
error=[]           #存储每次迭代后H的训练误差
for t in range(T):
    boot_strap_sampling=np.random.randint(0,m,m)
    Xbs=X[boot_strap_sampling]
    Ybs=Y[boot_strap_sampling]
    h=tree.DecisionTreeClassifier().fit(Xbs,Ybs)
    H.append(h)
    # 计算并存储当前步的训练误差
    H_pre+=h.predict(X)
    Y_pre=(H_pre>=0)*2-1
    error.append(sum(Y_pre!=Y)/m)
    

#>>>>>绘制训练误差变化曲线
plt.title('训练误差的变化')
plt.plot(range(1,T+1),error,'o-',markersize=2)
plt.xlabel('基学习器个数')
plt.ylabel('错误率')
plt.show()

#>>>>>观察结果
x1min,x1max=X[:,0].min(),X[:,0].max()
x2min,x2max=X[:,1].min(),X[:,1].max()
x1=np.linspace(x1min-(x1max-x1min)*0.2,x1max+(x1max-x1min)*0.2,100)
x2=np.linspace(x2min-(x2max-x2min)*0.2,x2max+(x2max-x2min)*0.2,100)
X1,X2=np.meshgrid(x1,x2)

for t in [3,5,11]:
    plt.title('前%d个基学习器'%t)
    plt.xlabel('密度')
    plt.ylabel('含糖量')
    # 画样本数据点
    plt.scatter(X[Y==1,0],X[Y==1,1],marker='+',c='r',s=100,label='好瓜')
    plt.scatter(X[Y==-1,0],X[Y==-1,1],marker='_',c='k',s=100,label='坏瓜')
    plt.legend()
    # 画基学习器划分边界
    for i in range(t):
        #由于sklearn.tree类中将决策树的结构参数封装于内部，
        #不方便提取，这里采用一个笨办法：
        #用predict方法对区域内所有数据点(100×100)进行预测，
        #然后再用plt.contour的方法来找出划分边界
        Ypre=predict([H[i]],X1,X2)
        plt.contour(X1,X2,Ypre,colors='k',linewidths=1,levels=[0])
    # 画集成学习器划分边界
    Ypre=predict(H[:t],X1,X2)
    plt.contour(X1,X2,Ypre,colors='r',linewidths=5,levels=[0])
    plt.show()
posted @ 2020-09-25 23:49  之始  阅读(3683)  评论(1)  编辑  收藏  举报