ABC292 解题报告

\(\text{By yeminghan}\)

Atcoder Beginner Contest 292

Contest link

My result

A - CAPS LOCK

没啥好说的。

string s;
void Solve()
{
	cin>>s;
	for(int i=0;i<s.size();i++)cout<<(char)(s[i]-32);
}

B - Yellow and Red Card

两黄染一红。

用一个变量统计罚牌的"quality"，黄牌 \(+1\)，红牌 \(+2\)，询问时判断其 quality 是否大于等于 \(2\)。

int n,q,op,x;
int a[105];
void Solve()
{
	cin>>n>>q;
	while(q--)
	{
		cin>>op>>x;
		if(op==1)a[x]++;
		if(op==2)a[x]+=2;
		if(op==3)
		{
			if(a[x]>=2)cout<<"Yes\n";
			else cout<<"No\n";
		}
	}
}

C - Four Variables

先预处理满足 \(xy=t\) 对于每个 \(t\) 的解的个数 \(t[]\)（通过枚举 \(x,y\) 可以证明是 \(O(n\log n)\) 的）。

然后答案就等于 \(\sum\limits_{i=1}^{n-1}t_it_{n-i}\)。

const int N=200000; 
int n;
ll ans;
ll t[N+5];
void Solve()
{
	cin>>n;
	for(int i=1;i<=n;i++)
		for(int j=1;i*j<=n;j++)t[i*j]++;
	for(int i=1;i<n;i++)ans+=t[i]*t[n-i];
	cout<<ans;
}

D - Unicyclic Components

按题意模拟即可。

const int N=200005; 
int n,m,u,v;
vector<int>to[N];
int V,E;
bool vis[N];
void dfs(int x)
{
	vis[x]=1;V++;
	E+=to[x].size();
	for(int i:to[x])
		if(!vis[i])dfs(i);
}
void Solve()
{
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		cin>>u>>v;
		to[u].push_back(v),to[v].push_back(u);
	}
	for(int i=1;i<=n;i++)
		if(!vis[i])
		{
			V=E=0;
			dfs(i);
			if(V*2!=E)return cout<<"No",void();
		}
	cout<<"Yes";
}

E - Transitivity

对于每个节点 \(i\)，他必须像他能到达的其他点连边。可以证明，不需要连更多的边。

可以 dfs 出每个点能到达的点的个数。时间复杂度 \(O(n^2)\)。

代码是从 D 改的，不信你看 \(N\) 是 \(20\)w 啊。

const int N=200005; 
int n,m,u,v;
vector<int>to[N];
bool vis[N];
int ans;
void dfs(int x)
{
	vis[x]=1;ans++;
	for(int i:to[x])if(!vis[i])dfs(i);
}
void Solve()
{
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		cin>>u>>v;
		to[u].push_back(v);
	}
	for(int i=1;i<=n;i++)
	{
		memset(vis,0,sizeof(vis));
		dfs(i);
	}
	cout<<ans-m-n;
}

F - Regular Triangle Inside a Rectangle

数学题？

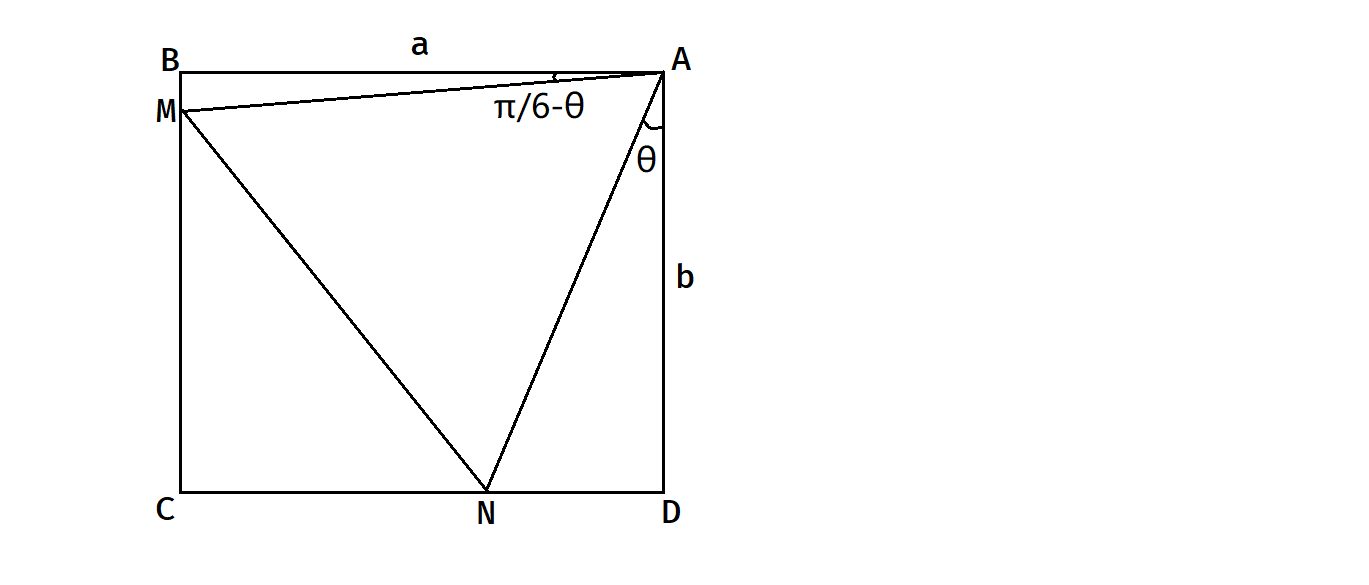
抱歉图画的丑

我们不妨假设 \(a\ge b\)。

可以证明，在最优解中，一定会让三角形的一个顶点与长方形的一个顶点重合。

我们可以二分 \(\theta\)（注意 \(\theta\) 的上限是 \(\dfrac{\pi}{6}\)），那么 \(AM=AN=\dfrac{b}{\cos\theta}\)，\(AB=AM\cos\angle BAM=\dfrac{b}{\cos\theta}\cdot\cos\left(\dfrac{\pi}{6}-\theta\right)\)。

只需判断是否有 \(AB\le a\)。

const double Pi=3.141592653589793238;
double a,b,l,r,mid;
void Solve()
{
	cin>>a>>b;
	if(a<b)swap(a,b);
	l=0,r=Pi/6.0;
	for(int i=1;i<=100;i++)
	{
		mid=(l+r)/2.0;
		double len=b/cos(mid);
		double siz=len*cos(Pi/6.0-mid);
		if(siz<=a)l=mid;else r=mid;
	}
	printf("%.15lf",b/cos(mid));
}