同态加密技术-Homomorphic Encryption
同态加密技术报告
成员:王妮婷 王静雯 郑爽
2020-03-02
前言
随着云计算的广泛应用, 特别是云平台上的大量电子商务交易, 如何安全有效地保护用户隐私与安全成为当今密码学研究领域的热点。若数据以明文形式进行存储则有可能将敏感数据暴露给云服务商, 会给用户机密数据带来一系列的安全问题。为解决这一问题, 同态加密方案应运而生, 利用全同态加密方案对用户数据进行加密, 再将密文发送到云端, 数据在云端可以进行一系列的上传、下载、删除、更新、检索等操作, 且操作的均是密文。该操作既避免了数据在传输过程中被拦截、复制、窜改或伪造等风险, 也避免了数据存储方将数据泄露或在服务器端被攻破的危险。
同态
同态是从一个代数结构(如:群、环或者向量空间)到同类代数结构的映射,它保持所有相关的结构不变。从数学的角度上讲,同态就是“保运算”。
举一个简单的例子:
考虑带加法运算的整数。保持加法不变的函数有如下性质:
f(a+b)=f(a)+f(b)
例如f(x)=3x就是这样的一个同态。因为 f(a+b)=3(a+b)=3a+3b=f(a)+f(b)。 且这个同态从整数映射回整数(整数的代数结构为群)。
同态加密技术
定义
同态加密的研究可以追溯到20世纪70年代,1978年Rivest等人在题为《On data banks and privacy homomorphic》中首次提出了同态加密的概念:允许用户直接 对密文进行特定的代数运算,得到数据仍是加密的结果,且与对明文进行同样的操作再将结果加密一样。
为了更好的理解该定义,用简易版的ElGamal加密方案为例:
若Elgamal加密方案的密文形式为:
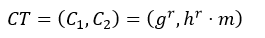
其中r是加密过程中选的一个随机数,g是一个生成元,h是公钥,m为对应的明文。
如果我们有两个密文CT1,CT2:

我们把这两个密文的第一部分相乘,第二部分相乘,会得到:
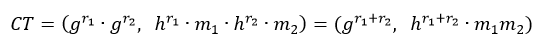
也就是说,相乘以后的密文正好是m1m2所对应的密文。这样,用户解密后得到的就是m1m2的结果了。
同态加密的主要类型
具有同态性质的加密函数是指两个明文a、b满足Dec(En(a)⊙En(b))=a⊕b的加密函数,其中En是加密运算,Dec是解密运算,⊙、⊕分别对应明文和密文域上的运算。
目前根据对其密文执行的数学运算的类型和频率的不同,将同态加密归纳为三种主要类型。
- 部分同态加密(PHE):过仅允许对加密值执行选择的数学函数来帮助敏感数据保持机密。这意味着可以在密文上无限次地执行一次操作。上述加密函数中,当⊕代表加法时,称该加密为加同态加密;当⊕代表乘法时,称该加密为乘同态加密;部分同态加密(关于乘法运算)是RSA加密算法的基础,RSA加密通常用于通过SSL / TLS建立安全连接。除此之外,常见的采用部分同态加密方案的算法还有ElGamal加密算法(具有乘法同态性)和Paillier加密算法(具有加法同态性)。
- 稍微同态加密(SHE):支持有限操作(例如,加法或乘法)直到某个复杂度的方案,但是这些操作只能执行一定次数。这是完全同态加密的先驱。
- 完全同态加密(FHE),又称全同态加密:仍处于开发阶段,但通过帮助保持信息安全且仍可访问,可以使功能与隐私保持一致。这种加密方案同时满足加同态和乘同态性质,能够使用任何有效的可计算函数(例如加法和乘法),并使安全的多方计算更有效。与其他形式的同态加密不同,它可以处理密文的任意计算。
总的来说,部分同态加密由于支持同态计算一种运算,比如乘法同态的RSA加密算法,由于它是一个确定性的公钥加密方案,因而不是语义安全的。具有较大的局限性。而全同态加密实现了在不解密的条件下对加密数据进行任何可以在明文上进行的运算,使得对加密信息仍能进行深入和无限的分析,而不会影响其保密性。但为提高全同态加密的效率,密码学界对其研究与探索仍在不断推进,这将使得全同态加密越来越向实用化靠近。
同态加密的构成
同态加密由四个部分组成, 分别为密钥的生成、同态加密、同态解密及同态赋值。
- 密钥的生成 :由安全参数 λ 生成 公钥 pk、私钥 sk;
- 同态加密 :给出指定明文 m∈{ 0, 1} * ,用公钥 pk 加密明文 m,得出密文 c;
- 同态赋值 :输入公 钥 pk,t 个输入的电路 C,一组密文 c = ( c1, …, ct ) ,输出 c* = evaluate( pk, C, c) , 且满足 dec( sk, c* ) = C( m1, …, mn ) 。
其中evaluate 算法是完全同态加密中最重要的部分,通过 evaluate可以对任意函数进行计算,输入都是密文。这里指全同态加密。
- 同态解密 :输入私钥sk 和密文 c 进行解密运算, 输出明文 m'。
为了更好的形象化这个同态加密的构成,以云场景下同态加密过程为例,简单明了:
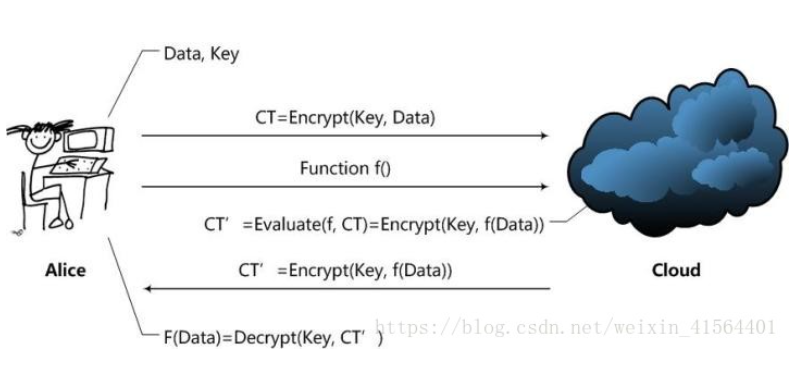
Alice通过Cloud,以Homomorphic Encryption(以下简称HE)处理数据的整个处理过程大致是这样的:
1)Alice对数据进行加密。并把加密后的数据CT发送给Cloud;
2)Alice向Cloud提交数据的处理方法,这里用函数f来表示;
3)Cloud在函数f下对密文数据进行处理,并且将处理后的结果CT‘发送给Alice;
4)Alice对数据CT’进行解密,得到结果。
同态加密技术的应用
同态加密技术在分布式计算环境下的密文数据计算方面具有比较广泛的应用领域,比如云计算、多方安全计算、匿名投票、密文检索与匿名访问等;除此之外,同态加密技术在数据挖掘隐私保护方面也有相应的应用。
安全云计算与委托计算
同态技术在该方面的应用可以使得我们在云环境下,充分利用云服务器的计算能力,实现对明文信息的运算,而不会有损私有数据的私密性。例如医疗机构通常拥有比较弱的数据处理能力,而需要第三方来实现数据处理分析以达到更好的医疗效果或者科研水平,这样他们就需要委托有较强数据处理能力的第三方实现数据处理(云计算中心),但是医院负有保护患者隐私的义务,不能直接将数据交给第三方。在同态加密技术的支持下,医疗机构就可以将加密后的数据发送至第三方,待第三方处理完成后便可返回给医疗结构。整个数据处理过程、数据内容对第三方是完全透明的。
文件存储与密文检索
用户可以将自己的数据加密后存储在一个不信任的远程服务器上,日后可以向远程服务器查询自己所需要的信息,存储与查询都使用密文数据,服务器将检索到的密文数据发回。用户可以解密得到自己需要的信息,而远程服务器却对存储和检索的信息一无所知。此种方法同样适用于搜索引擎的数据检索。
基于同态加密技术的隐私保护KNN分类算法
KNN 算法是数据挖掘技术中比较常用的分类算法, 由于其实现的简单性, 在很多领域得到了广泛的应用。KNN 分类算法的主要思想是: 先计算待分类样本与已知类别的训练样本之间的距离或相似度,找到距离或相似度与待分类样本数据最近的 K 个邻居; 再根据这些邻居所属的类别来判断待分类样本数据的类别。如果待分类样本数据的 K 个邻居都属于一个类别,那么待分类样本也属于这个类别; 否则,对每一个候选类别进行评分,按照某种规则来确定待分类样本数据的类别。
Kumar 等人提出了基于最近邻居查找的隐私保护方法, 并利用同态加密技术在数据用户终端对私有数据进行加密。尽管训练样本中的数据是加密后的数据,根据同态加密的性质,这些数据仍然可以用于计算最近邻居。在计算过程中,需要第三方参与,该第三方被认为是一个准诚信方。
Zhu Jian-ming提出了基于同态加密和EIGamal 加密系统的隐私保护 KNN 分类挖掘方法,在计算KNN 时利用同态加密技术以保证数据的隐私性,该方法也是假定在准诚信的环境下。
总结
优势
- 不必对每一个密文解密后再计算而花费高昂的计算代价。
- 可以实现无密钥方对密文的计算,密文计算无须经过密钥方,既可以减少通信代价,又可以转移计算任务。
- 第三方为明文未知,提高了信息的安全性。
- 对密文计算后解密的结果与明文进行同样运算的结果一致,保证了运算的正确性。
不足
- 同态加密技术目前的难度在于效率,不能达到一定效率的同态加密实用性并不高。
- 满足同态加密的算法并不容易找到。
参考文献
《同态加密隐私保护数据挖掘方法综述》钱萍等
《同态加密研究进展综述》李浪等
“同态加密”维基百科 https://zh.wikipedia.org/zh-hans/%E5%90%8C%E6%80%81%E5%8A%A0%E5%AF%86
博客 https://blog.csdn.net/weixin_41564401/article/details/82777335 等......

