【题解】 bzoj3894: 文理分科 (网络流/最小割)
Solution:
- 首先这是一个网络流,应该还比较好想,主要就是考虑建图了。
- 我们来分析下题面,因为一个人要么选文科要么选理科,相当于两条流里面割掉一条(怎么想到割我也不知道,颓的题解),那么我们就可以从原点连向每个人,流量为文科愉悦值,然后每个人连向汇点,流量为理科愉悦值。因为要构成最小割,就相当与每条路径一定割一条。
- 然后我们考虑周围人那个情况,拿文科做例子,我们可以从原点连到一个新点,流量为这个额外愉悦值,然后把这个新节点连向这个周围的五个点(或者四/三个点),理科反过来连到汇点即可,至于为什么这样子可以。下面是解释:
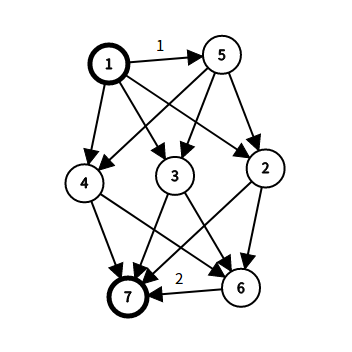
我们假设割掉所以与原点(\(1\))与文科特殊情况的新点(\(5\))的那条边(假设为边\(A\),图中标记为\(1\))割掉,如果要不练通,显然所有与汇点相连的边都会要割掉,这时候这条\(A\)边显然可以不割,那么这两条边是不会同时留下的(这其实也是显然) - 然后我们可以求出最小割,每个割表示的是不选哪种情况,那么最小割就是舍弃的愉悦值最小的情况,我们拿所有愉悦值之和减去最小割即可
- 貌似有点点卡常,用当前弧优化可以解决
- 网络流/最小割/费用流的题要多做才会知道建模的套路,不然真的想不到qwq
Code:
//It is coded by ning-mew on 6.28
#include<bits/stdc++.h>
#define FOR for(int i=1;i<=n;i++) for(int j=1;j<=m;j++)
using namespace std;
const int maxn=507,INF=1e9+7;
int n,m,S=0,T=maxn*maxn*6-1,ANS=0;
int head[maxn*maxn*6],cnt=-1,last[maxn*maxn*6];
struct Edge{int nxt,to,dis;}edge[maxn*maxn*25];
int art[maxn][maxn],sce[maxn][maxn];
int same_art[maxn][maxn],same_sce[maxn][maxn];
int add_x[5]={0,0,0,1,-1},add_y[5]={0,1,-1,0,0};
int Node(int x,int y,int num){
return n*m*(num-1)+(x-1)*m+y;
}
void add(int from,int to,int dis){
edge[++cnt].nxt=head[from];edge[cnt].to=to;
edge[cnt].dis=dis;head[from]=cnt;
}
void Add(int from,int to,int dis){
//cout<<from<<' '<<to<<' '<<dis<<endl;
add(from,to,dis);add(to,from,0);return;
}
struct Network{
int depth[maxn*maxn*6],mark[maxn*maxn*6];
void clear(){
memset(depth,0,sizeof(depth));
memset(mark,0,sizeof(mark));
}
bool bfs(int x){
queue<int>Q;while(!Q.empty())Q.pop();
Q.push(S);depth[S]=1;mark[S]=x;
while(!Q.empty()){
int u=Q.front();Q.pop();
for(int i=head[u];i!=-1;i=edge[i].nxt){
int v=edge[i].to;
if(mark[v]!=x&&edge[i].dis>0){
mark[v]=x;depth[v]=depth[u]+1;
Q.push(v);
}
}
}if(mark[T]==x)return true;return false;
}
int dfs(int u,int dist){
if(u==T)return dist;int d=0;
for(int &i=last[u];i!=-1;i=edge[i].nxt){
int v=edge[i].to;
if(mark[v]==mark[u]&&depth[v]==depth[u]+1&&edge[i].dis>0){
d=dfs(v,min(edge[i].dis,dist));
if(d){
edge[i].dis-=d;edge[i^1].dis+=d;
return d;
}
}
}return 0;
}
int Dinic(){ clear();
int ans=0,d=0,x=2;
while(bfs(++x)){
d=dfs(S,INF);
while(d){/*cout<<"Dinic:"<<d<<endl;*/ans+=d;d=dfs(S,INF);}
for(int i=0;i<=m*n*4;i++)last[i]=head[i];last[T]=head[T];
}return ans;
}
}Net;
int main(){
scanf("%d%d",&n,&m);
memset(head,-1,sizeof(head));
FOR scanf("%d",&art[i][j]),ANS+=art[i][j],
Add(S,Node(i,j,1),art[i][j]),Add(Node(i,j,1),Node(i,j,2),INF);
FOR scanf("%d",&sce[i][j]),ANS+=sce[i][j],
Add(Node(i,j,2),T,sce[i][j]);
FOR {
scanf("%d",&same_art[i][j]);ANS+=same_art[i][j];
Add(S,Node(i,j,3),same_art[i][j]);
for(int k=0;k<=4;k++){
int ii=i+add_x[k],jj=j+add_y[k];
if(ii>0&&ii<=n&&jj>0&&jj<=m){
Add(Node(i,j,3),Node(ii,jj,1),INF);
}
}
}
FOR {
scanf("%d",&same_sce[i][j]);ANS+=same_sce[i][j];
Add(Node(i,j,4),T,same_sce[i][j]);
for(int k=0;k<=4;k++){
int ii=i+add_x[k],jj=j+add_y[k];
if(ii>0&&ii<=n&&jj>0&&jj<=m){
Add(Node(ii,jj,2),Node(i,j,4),INF);
}
}
}
printf("%d\n",ANS-Net.Dinic());
return 0;
}
博主蒟蒻,随意转载。但必须附上原文链接:http://www.cnblogs.com/Ning-Mew/,否则你会终生找不到妹子!!!


