浅谈字符串
0x01 浅谈 KMP
问题简述:求字符串 s1 在给定字符串 s2 中所有的出现。
0x11 前缀数组
写在前面
本人参考多方资料,发现《算法竞赛进阶指南》、《算法竞赛入门经典》等书对于所谓的&next&数组描述并不是很清楚,容易给读者造成“应当这么设定,这么做”却不明白其原有的真谛。后本人在OI wiki上看到了他们对于前缀数组的描述,认为其讲解更易让读者理解。
当然,本文综合多方资料,下面将讲述我本人的理解。
定义与粗略算法
设字符串 \(s[0:n]\) 前缀数组 \(p[0:n]\),其中 \(p[i]\) 的含义为 \(s\) 子串 \(s[0:i]\) 中相等的真前缀与真后缀的最长长度(真前缀和真后缀即不能为字符串本身),即:\(p[i] = \max\left\{j\ \vert \ s[0:j - 1] = s[i - j + 1: j]\right\}\)。
由定义,可以两层循环枚举 \(i,\ j\), 并判断前缀与后缀是否相等求出 \(p[i]\),时间复杂度显然是 \(O(n^2)\) 的。
优化1
已经求出 \(p[i]\),当枚举到 \(s[i + 1]\) 时,已知 \(s[0:p[i]-1]=s[i-p[i]+1:i]\),则显然:若\(s[\ p[i]\ ]=s[i+1]\),则\(p[i+1]=p[i]+1\)。
- 注:上面之所以是 \(s[\ p[i]\ ] = s[i+1]\),是因为字符数组下标从 \(0\) 开始计算。
优化2
在优化1不满足时,若存在某一仅次于 \(p[i]\) 的 j 满足前缀数组的性质,即:\(s[0:j - 1] = s[i - j + 1: i]\) 且 \(j\) 的大小仅次于 \(p[i]\)。这时,若\(s[j]=s[i]\),则 \(p[i+1]=j\)。
按照 \(p[i]\) 的定义,上述思想并不难理解。但是算法的关键在于如何寻找次大的 \(j\)。
我个人认为 OI Wiki 上对于这一部分内容解释的相当不错,下面的内容部分引用自 OI wiki。
首先:有\(s[0:j - 1]=s[i - j + 1: i]\) 且 \(s[0:p[i] - 1] = s[i - p[i] + 1:i]\),可以看出 \(s[0:j-1]\) 是 \(s[0:p[i]-1]\) 的子串。不难得到以下关系:
- 注:这边数到 \(s[p[i] - 1]\) 的原因同样是因为字符串下标从 \(0\) 开始计数,以后将不再赘述,请读者注意。
下面的示意图可以很好的帮助理解上述公式(思路来源于OI wiki):
上述公式中:\(s[0:j - 1] = s[p[i] - j: p[i] - 1]\) 描述的是什么意思呢?回想 \(p[i]\) 的定义不难发现,满足 \(s[0:j - 1] = s[p[i] - j: p[i] - 1]\) 最大的 \(j\) 即为 \(p[\ p[i]-1]\)。故可得:
此时,只需判断是否满足 \(s[j]=s[i+1]\)。若满足,则\(p[i]=j+1\)。
基于这个思想出发,若不满足,我们只需再求次于 \(j\) 的长度,不妨记为 \(j^{(2)}\),初次求出的 \(j\) 记为 \(j^{(1)}\),则只要不满足 \(s[j^{(n)}]=s[i+1]\),则迭代 \(j^{(n+1)}=p[j^{(n)}-1]\),直至 \(j=0\)。按照这个想法,其实我们可以认为 \(j^{(0)}=p[i]\);
算法实现如下:
// 显然:p[0] = 0
for(int i = 1; i < slen; ++i) { // slen为字符串长度
int j = p[i - 1];
while(j and s[i] != s[j]) j = p[j - 1];
if(s[i] == s[j]) ++j;
p[i] = j;
}
发现当循环进入下一层时,\(j\) 值不变,没必要每次循环都定义并幅值,可以将算法简化:
for(int i = 1, j = 0; i < slen; ++i) {
while(j and s[i] != s[j]) j = p[j - 1];
if(s[i] == s[j]) ++j;
p[i] = j;
}
- 注:两段算法都是默认为 \(p[i-1]\) 已求出,现在枚举到 \(i\),读者自行变通便可以理解这与上述理论并无差异。
0x12 KMP 字符串匹配
做法1
根据前缀数组的含义,新建一个字符串 \(s\)。若把模式串 \(s_1\) 作为新串 \(s\) 前缀,文本串 \(s_2\) 作为新串 \(s\) 后缀,\(s_1\) 和 \(s_2\) 中间用一个未出现的字符隔开。则:对于新串 \(s=s_1+'\#'+s_2\),设 \(s1\) 长度为 \(n\),\(s\) 长度为 \(slen\),对 \(s\) 进行前缀数组 \(p[0:slen-1]\) 计算,有:
字符串 \(p\) 在 \(t\) 中出现,当且仅当 \(p[i]=n,i>n+1\)。此时,\(s_1\) 出现在 \(s_2\) 中的位置为 \(i-2n\)。(数组下标从0开始,注意 \(s\) 串中还插入了一个分割符)
这种做法有一个比较重要的前提条件,就是要已知哪些字符会在 \(s_1\) 和 \(s_2\) 中出现,以便寻找分隔符。而此条件绝大部分题目都会给出,所以本做法具有普适性。这个做法很好的利用了前缀数组定义,也是比较好理解的做法。
- 注:思路来源于 OI wiki。
完整代码如下:
#include <bits/stdc++.h>
#define N 2000005 // 注意 s1+s2 长度
using namespace std;
int pi[N];
void kmp(string s1, string s2) {
string s = s1 + "*" + s2;
int l = s1.size() + 1, r = s.size();
int n = s1.size();
for(int i = 1, j = 0; i < r; ++i) {
while(j and s[i] != s[j]) j = pi[j - 1];
if(s[i] == s[j]) ++j;
pi[i] = j;
}
for(int i = l; i < r; ++i)
if(pi[i] == n) printf("%d\n", i - 2 * n + 1); // 题目数组编号从 1 开始
for(int i = 0; i < n; ++i)
printf("%d ", pi[i]);
}
int main() {
string s1, s2;
cin >> s1 >> s2;
kmp(s2, s1);
return 0;
}
做法2
这个做法就是普遍出现在各算法竞赛资料书上的做法,即不合并 \(s_1\) 和 \(s_2\),在求出 \(s_1\) 的 \(p\) 数组后,继续计算剩余的 \(p\) 数组。这个解释是本人的理解,可能与各个算法书上描述有所差异,但同时笔者认为这样的描述可以避免对“模式串自己匹配自己”等想法感到玄学,而且更加便于理解。
为了区别原先的 \(p\) 数组,我们定义后续的 \('p'\) 数组为 \(f[0:m-1]\),此后的 \(i\) 为匹配到 \(s_2\) 中第 \(i\) 个字符。可见,\(f[i]\) 数组定义为:满足 \(s1[0:j-1]=s2[i-j+1:i]\) 的最大的 \(j\)。
考虑 \(i+1\),已知满足 \(s1[0:f[i]-1] = s2[i-f[i]+1:i\ ]\)。
-
若\(s1[\ f[i]\ ] = s2[i+1]\),显然有 \(f[i+1]=f[i]+1\);
-
若不满足上述条件,寻找次大的 \(j^{(1)}\),使得 \(s1[0:j^{(1)}]=s2[i-j^{(1)}+1:i]=s1[f[i]-j^(1):f[i]-1]\),根据前缀数组的定义 \(j^{(1)}=p[f[i]-1]\)。若仍不满足 \(s1[j^{(1)}]=s2[i+1]\),则重复迭代。显然有 \(j^{(n+1)}=p[j^{(n)}-1]\),直至 \(j=0\)。
-
开始时,可设 \(j=f[i]\)。
-
若 \(j=n\),即上一次已经求出 \(s1\) 在 \(s2\) 中的一次出现,仍要寻找次大的 \(j\),同上述步骤。
下面的示意图可以帮助理解上述想法:
可以看出上述算法其实与第一种做法并无太大差异。
完整代码如下:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
char s1[N], s2[N];
int p[N], f[N];
int main() {
scanf("%s%s", s2, s1);
int n = strlen(s1), m = strlen(s2);
for(int i = 1, j = 0; i < n; ++i) {
while(j and s1[i] != s1[j]) j = p[j - 1];
if(s1[i] == s1[j]) ++j;
p[i] = j;
}
for(int i = 0, j = 0; i < m; ++i) {
while(j and s2[i] != s1[j]) j = p[j - 1];
if(s2[i] == s1[j]) ++j;
f[i] = j;
if(f[i] == n) {
printf("%d\n", i - n + 2);
j = p[j - 1];
}
}
for(int i = 0; i < n; ++i)
printf("%d ", p[i]);
return 0;
}
写在后面
相对于做法2,做法1显然更好理解,并且充分体现了前缀数组的应用,笔者建议读者熟练掌握第一种方法,理解第二种方法即可。当然,读者亦可不认可笔者的说法,对于信息竞赛而言两种做法本质上并没有区别,读者掌握其一即可。
0x02 Z函数|扩展KMP
题意简述:对于长度为 \(n\) 的字符串 \(s[0:n-1]\),设 \(z[i]\) 表示 \(s\) 和 \(s[i:n-1]\) (即 \(s\) 以 \(s[i]\) 开头的后缀)的最长公共前缀(\(LCP\))的长度。求 \(z\)。
- 奇怪的是,很多博客(包括洛谷原题)认为 \(z[0]=n\),而 OI wiki 则写明 \(z[0]=0\)。不论如何,以题目要求为准。以大部分博客和题目而言,认为 \(z[0]=n\) 较为准确。
0x21 朴素算法
暴力比较,时间复杂度显然是 \(O(n^2)\) 的,不过多赘述。
0x22 线性算法
优化
设当前枚举到 \(i\),在此之前,我们已经计算好 \(z[0:i-1]\),设 \(j<i\) 且满足 \(j+z[j]-1\) 最大,即 \(s[0:z[j]-1]=s[j:j+z[j]-1]\)。设 \(l=j,r=j+z[j]-1\)
此优化的目的在于:
- 若 \(l≤i≤r\),则肯定有 \(s[i:r]=s[i-l:r-l]\)。回想刚刚学过的 \(KMP\),可以发现二者的思想非常像。根据 \(z\) 函数的定义,只要 \(z[l-i]<r-i+1\),则 \(z[i]=z[i-l]\)。
为什么?如果 \(z[i-l]<r-i+1\),即 \(i+z[i-l]-1<r\),说明 \(s[i+z[i-l]:r]\) 这一段是不匹配的。下面的示意图可以帮助读者理解这一性质。
另外的,若 \(z[i-l]≥r-i+1\),此时:只能保证 \(s[i,r]\) 与 \(s\) 前缀匹配,此时应当继续比较判断 \([r+1,n-1]\) 是否能和 \(s\) 的前缀继续匹配,从而确定 \(z[i]\)。
-
若 \(i>r\),直接进行暴力比较。
-
计算完后,更新维护 \(l,r\)。
代码如下:
for(int i = 1, l = 0, r = 0; i < slen; ++i) {
if(i <= r and z[i - l] < r - i + 1) z[i] = z[i - l];
else {
z[i] = max(0, r - i + 1);
while(i + z[i] < slen and s[z[i]] == s[i + z[i]]) ++z[i];
}
if(i + z[i] - 1 > r) l = i, r = i + z[i] - 1;
}
时间复杂度分析
观察内层 \(while\) 循环,每进行一次循环必将使 \(r\) 增大 \(1\),且 \(r<n\),即 \(while\) 循环最多进行 \(n\) 次,故时间复杂度 \(O(n)\)。
模板题分析
设 \(a\) 为文本串,\(b\) 为模式串(与洛谷题目相同)。不妨设新串 \(s=b+'\#'+a\),即将 \(b\) 作为新串前缀,\(a\) 作为新串后缀。直接对新串进行 \(z\) 函数计算即可。这个思想和 \(KMP\) 的做法1非常类似,这也是笔者推荐熟练掌握这种方法的原因,其背后更重要的是思想方法。注意 \(b\) 和 \(a\) 之间应当用一个不会出现的字符隔开。
完整代码如下:
#include <bits/stdc++.h>
#define N 40000005
using namespace std;
int z[N];
void z_func(string s1, string s2) {
string s = s1 + '#' + s2;
int slen = s.size(), n = s1.size();
for(int i = 1, l = 0, r = 0; i < slen; ++i) {
if(i <= r and z[i - l] < r - i + 1) z[i] = z[i - l];
else {
z[i] = max(0, r - i + 1);
while(i + z[i] < slen and s[z[i]] == s[i + z[i]]) ++z[i];
}
if(i + z[i] - 1 > r) l = i, r = i + z[i] - 1;
}
long long ans = 0;
z[0] = n;
for(int i = 0; i < n; ++i)
ans ^= 1LL * (i + 1) * (z[i] + 1);
printf("%lld\n", ans);
ans = 0;
for(int i = n + 1; i < slen; ++i)
ans ^= 1LL * (i - n) * (z[i] + 1);
printf("%lld\n", ans);
}
int main() {
ios::sync_with_stdio(false);
string s1, s2;
cin >> s1 >> s2;
z_func(s2, s1);
return 0;
}
0x30 字典树|Trie
模板题:洛谷-P8306 【模板】字典树
题意简述:给定 \(n\) 个文本串和 \(q\) 个询问,每次询问一个模式串“是否出现过”或“是否作为某个或某些文本串的前缀”等。
0x31 实现原理和方法
字典树的一个重要思想是,建立一颗树,树上的一条由根节点到叶节点的路径代表一个字符串,这个路径的每条边依次上存字符串的各个字符。
下图展示了一颗简单的 \(\text{Trie}\):
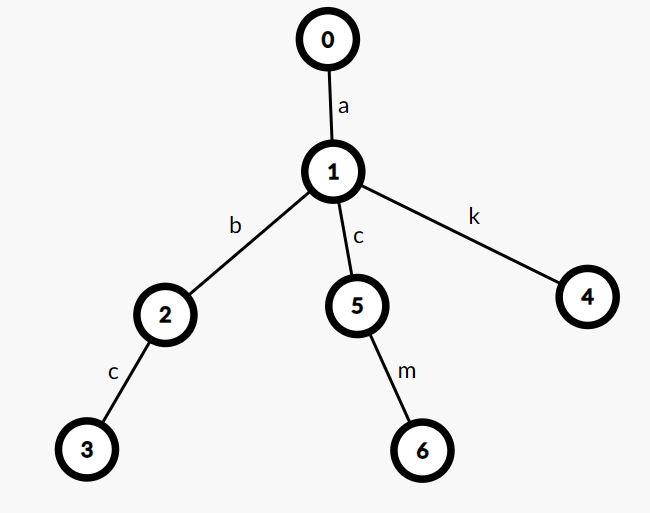
(图片为本人原创,转载请注明出处)
- 举例而言,\(\text{Trie}\) 上 \(0\to 1\to 5\to 6\) 这一条路径就代表了字符串 \(acm\)。
理解了这一点后,在树上插入字符串便不难实现,代码如下:
void insert(char *s) {
int size = strlen(s), p = 0;
for(int i = 0, d; i < size; ++i) {
d = idx(s[i]); // idx 为根据题目要求求出对应字符编号的函数,读者可自行实现
if(!trie[p][d]) trie[p][d] = ++tot;
p = trie[p][d];
}
exist[p] = 1;
}
查找字符串是否存在代码如下:
int find(char *s) {
int size = strlen(s), p = 0;
for(int i = 0, d; i < size; ++i) {
d = idx(s[i]);
if(!trie[p][d]) return 0;
p = trie[p][d];
}
return exist[p];
}
- 值得注意的是,根据题目要求不同。在插入和查找时维护的信息也不尽相同。这一点在洛谷的模板题就是很好的体现。
0x32 模板题解析
洛谷上的模板题要求求出模式串作为文本串前缀出现的次数,在建树时维护一个 \(\text{cnt}\) 数组,记录以以每个节点为结尾的子串个数即可。
完整代码如下:
#include <bits/stdc++.h>
using namespace std;
const int N = 3e6 + 5;
int trie[N][62], cnt[N], tot;
int idx(char c) {
if(c >= 'a' and c <= 'z') return c - 'a';
else if(c >= 'A' and c <= 'Z') return c - 'A' + 26;
return c - '0' + 52;
}
void insert(char *s) {
int size = strlen(s), p = 0;
for(int i = 0, d; i < size; ++i) {
d = idx(s[i]);
if(!trie[p][d]) trie[p][d] = ++tot;
p = trie[p][d];
cnt[p]++;
}
}
int find(char *s) {
int size = strlen(s), p = 0;
for(int i = 0, d; i < size; ++i) {
d = idx(s[i]);
if(!trie[p][d]) return 0;
p = trie[p][d];
}
return cnt[p];
}
char s[N];
int main() {
int T, n, q;
scanf("%d", &T);
while(T--) {
scanf("%d %d", &n, &q);
while(n--) {
scanf(" %s", s);
insert(s);
}
while(q--) {
scanf(" %s", s);
printf("%d\n", find(s));
}
for(int i = 0; i <= tot; ++i)
for(int j = 0; j < 62; ++j)
trie[i][j] = 0;
for(int i = 1; i <= tot; ++i)
cnt[i] = 0;
tot = 0;
}
return 0;
}
0x40 AC自动机
模板题:洛谷-P5357 【模板】AC 自动机(二次加强版)
题意简述:对于若干个模式串(可能相同),求每个模式串在文本串中的出现次数。
0x41 构建失配指针
定义与构建方法
与 \(\text{KMP}\) 类似,对于多个模式串,建立一棵 \(\text{Trie}\),设失配数组 \(fail[0:cnt]\) (\(cnt\) 为字典树节点个数),对于节点 \(i\)(不为 \(0\)),其 \(fail[i]\) 的含义为树上路径 \(0\to fail[i]\) 为 \(0\to trie[i]\) 的最长后缀。回想 \(\text{KMP]\) 的 \(p\) 前缀数组定义,可以发现二者具有类似之处。不同的是,\(0 \to fail[i]\) 可能不是 \(0\to trie[i]\) 字符串所对应的前缀,但总是这若干个字符串的前缀。换句话说,\(fail\) 数组与 \(p\) 数组的思想还是异曲同工的。
那么,考虑对于某个节点 \(x\),其父亲 \(p\) 的失配指针已经求出,其通通过字符 \(c\) 指向 \(x\) (\(x=trie[p,c]\)),考虑求出 \(x\) 的失配指针,显然有 \(0\to fail[p]\) 所对应字符串是 \(0\to p\) 对应字符串的最长前缀:
- 若 \(trie[fail[p], c]\) 存在,则 \(fail[x]=trie[fail[p], c]\)。显然成立,这与前缀数组的匹配思想是一致的。
- 解释:\(0\to fail[p]\) 所代表字符串是 \(0\to p\) 所代表字符串的最长后缀,而 \(p\to x\) 这条边代表字符 \(c\),\(fail[p] \to trie[fail[p], c]\) 这条边也代表字符 \(c\)。所以 \(0\to trie[fail[p], x]\) 是 \(0\to x\) 的最长后缀。
- 若 \(trie[fail[p],x]\) 不存在,则继续考虑 \(trie[fail[faik[p]], c]\) 是否存在,重复 \(1\) 的判断直至跳到根节点。
下图展示了 \(\text{i he his she hers}\) 四个模式串组成的 \(\text{Trie}\) 以及对应的失配指针。
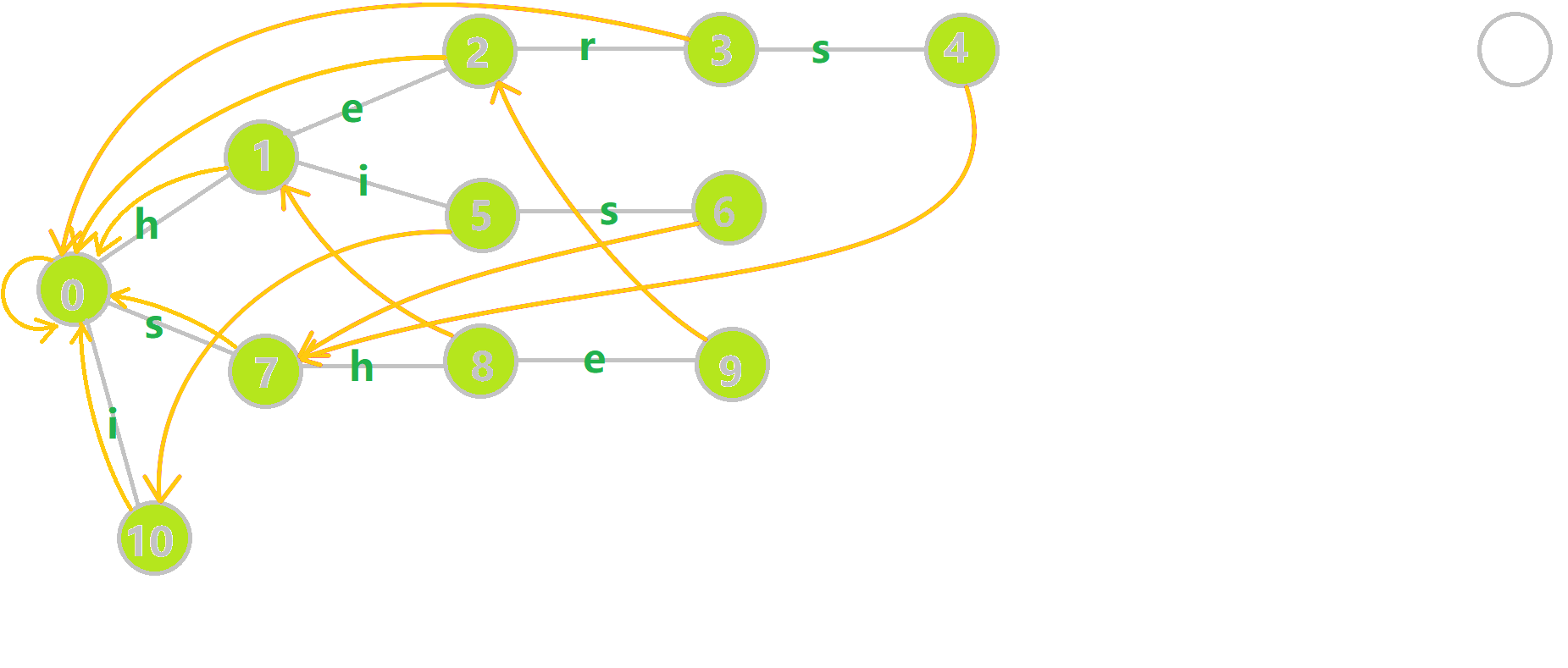
(图源 OI wiki,如有侵权请联系本人删除)
读者可以根据图自行理解或模拟上述构建规则。
构建优化
上述构建规则中第二条需要使用一个 \(while\) 循环一直跳到满足条件(或根节点)位置,如果多次重复访问会很消耗时间。
- 例子是有多个位置的失配指针指向同一个节点,但是这个节点均没有(对应)子节点,则求这多个位置的失配指针时,会重复访问。
而上述构建其实基于一个很重要的条件,即深度小于 \(x\) 节点的所有 \(fail\) 指针均已求出。这种情况下,对于访问到的某一节点 \(x\) (父节点为 \(p\),代表边为 \(c\))而言,若 \(trie[x, c]\) 不存在,则不妨令 \(trie[x, c]=trie[fail[p], c]\),即记录下若要跳转,这个不存在的子节点会跳转到的节点编号。这样,只要 \(trie[p,c]\) 存在,则直接令 \(fail[x]=trie[fail[p], c]\)即可。
这是因为:若 \(trie[fail[p], c]\) 原本就存在,则符合条件 \(1\);若 \(trie[fail[p], c]\) 原先不存在,则经过刚刚的操作,我们已经记录了 \(trie[fail[fail[p]], c]\) 会跳转到的位置(\(fail[p]\) 的深度小于 \(x\);若深度不小于 \(x\),则 \(0\to trie[fail[p],c]\) 长度比 \(0\to x\) 长而显然无法成为后缀)。这样就节约了大量时间。同时,在部分改变 \(\text{Trie}\) 结构的情况下,并不改变其记录的模式串。
要实现这样的算法,根据按照深度从小到大访问,考虑 \(\text{bfs}\)。代码如下:
void getfail() {
queue <int> q;
for(int i = 0; i < 26; ++i)
if(trie[0][i]) q.push(trie[0][i]);
while(q.size()) {
int x = q.front();
q.pop();
for(int i = 0; i < 26; ++i) {
if(trie[x][i]) {
fail[trie[x][i]] = trie[fail[x]][i];
q.push(trie[x][i]);
} else trie[x][i] = trie[fail[x]][i];
}
}
}
- 并且:由于对于每一个节点, \(fail\) 指针都是唯一且指向深度小于自己的节点(根节点除外),故 \(fail\) 指针所构成了一张 \(\text{DAG}\) (有向无环图)。
0x42 查询
在插入时,记录每个字符串插入的尾节点,即可在改变 \(\text{Trie}\) 的情况下找到每一个模式串。
插入和查询代码如下:
void insert(char *s) {
int size = strlen(s), p = 0;
for(int i = 0, c; i < size; ++i) {
c = s[i] - 'a';
if(!trie[p][c]) trie[p][c] = ++cnt;
p = trie[p][c];
}
End[p]++;
}
int query(char *s) {
int size = strlen(s), ans = 0, p = 0;
for(int i = 0; i < size; ++i) {
p = trie[p][s[i] - 'a'];
for(int j = p; j and ~End[j]; j = fail[j])
ans += End[j], End[j] = -1;
}
return ans;
}
对于查询代码的解释:
对于某一出现在文本串中模式串,其后缀也一定出现在文本串中。而顺序匹配时,是前缀匹配,忽略了后缀的计算。此时使用 \(fail\) 指针跳转至每一后缀,此后缀可能是完整的模式串也可能只是模式串的一部分。若是完整的模式串, \(End\) 不为 \(0\),否则为 \(0\)。
这样就是实现查询。
0x43 优化
注意到:查询时仍可能出现构造失配指针时“重复跳转”的情况,其最坏时间复杂度相当高,在部分题目会被卡掉。
但同时注意到,\(fail\) 数组构成一张 \(\text{DAG}\),对于此 \(\text{DAG}\) 上一边 \(x\to y\),显然 \(y\) 节点对于答案的贡献是其所有前驱节点对答案贡献之和(字典树上 \(0\to y\) 是 \(0\to x\) 的后缀),可以使用拓扑排序进行优化。查询时只需记录每个“前驱节点”的贡献即可,并在构建 \(fail\) 图时记录每个节点的入度。
模板题完整代码如下:
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10, M = 2e6 + 10;
int trie[N][26], End[N], fail[N], id[N], cnt;
void insert(char *s, int num) {
int size = strlen(s), p = 0;
for(int i = 0; i < size; ++i) {
int c = s[i] - 'a';
if(!trie[p][c]) trie[p][c] = ++cnt;
p = trie[p][c];
}
if(!End[p]) End[p] = num;
id[num] = End[p]; // 可能有重复字符串
}
int vis[N], ans[N], in[N];
void getfail() {
queue <int> q;
for(int i = 0; i < 26; ++i)
if(trie[0][i]) q.push(trie[0][i]);
while(q.size()) {
int x = q.front();
q.pop();
for(int i = 0; i < 26; ++i) {
if(trie[x][i]) {
fail[trie[x][i]] = trie[fail[x]][i];
in[trie[fail[x]][i]]++; // 记录入度
q.push(trie[x][i]);
} else trie[x][i] = trie[fail[x]][i];
}
}
}
void query(char *s) {
int size = strlen(s), p = 0;
for(int i = 0; i < size; ++i) {
p = trie[p][s[i] - 'a'];
vis[p]++; // 记录前驱节点贡献,其所有后缀在 fail 树上都是它的子节点(后继)
}
}
void topo() {
queue <int> q;
for(int i = 1; i <= cnt; ++i)
if(!in[i]) q.push(i);
while(q.size()) {
int x = q.front(), y;
q.pop();
ans[End[x]] = vis[x]; // 只有完整的模式串才有答案,否则都是对 ans[0] 赋值
y = fail[x];
vis[y] += vis[x]; // 计算贡献
if(!--in[y]) q.push(y);
}
}
char s[M];
int main() {
int n;
scanf("%d", &n);
for(int i = 1; i <= n; ++i)
scanf(" %s", s), insert(s, i);
getfail();
scanf(" %s", s);
query(s);
topo();
for(int i = 1; i <= n; ++i) printf("%d\n", ans[id[i]]);
return 0;
}

