再谈 FTT 与 NTT

前言

扯淡

之间写了一篇比较扯的博客 \(FFT/NTT\)，其实里面很多东西解释的有点复杂，基于本人对 \(FFT\) 更深入理解的情况下，再次写下这一篇博客。

此篇博客出于两个目的，一是为了巩固记忆，二是希望对 \(FFT/NTT\) 有初步了解的同学能更好理解算法。

阅读本文的一些要求

1、了解卷积（起码是多项式乘法）。

2、 有一定的数学基础。

3、 有较好的代码实现能力和思维能力。

• 如果不满足第 \(1\) 或 \(2\) 点，可以考虑阅读我上文所给出的博文；至于第三点，自己提升吧……

再探FFT

step1：优化过程

给定多项式 \(A(x),B(x)\)，不妨设 \(\displaystyle A=\sum_{i=0}^n a_ix^i\)，\(\displaystyle B=\sum_{i=0}^n b_ix^i\)，求 \(A*B\) 的每项系数。

此问题暴力算法为 \(O(n^2)\) 的复杂度，正常水平的同学能够很轻松的实现。

但是面对数据较大的情况，显然暴力算法是无法满足需求的，应当考虑卷积的过程优化：

我们知道平面直角坐标系上 \(n\) 个点能恰好表示一个 \(n\) 次函数。显然 \(n\) 次函数的表达式种有 \(n\) 个未知数，则 \(n\) 个点创造了 \(n\) 个一元 \(n\) 次方程，这样便可以求出整个 \(n\) 次函数。因为上面的式子其实也是可以看做函数的（只求系数，也就是对应的未知数），所以我们考虑把用点来表示上面的多项式。

定义多项式\(F(x)\)：

我们知道，\(1\)个n元一次方程最少需要\(n\)个式子求解，而我们把系数表达\(F(x)\)抽象为一个函数\(F(x)\)，那么这个函数至少需要\(n+1\)个点确定下来，那么我们任取\(n+1\)个不同的数构成集合\(U={k_1,k_2,…,k_{n+1}}\)，对\(F(x)\)分别求值得到一个新的集合，那么将两个集合合并成点集，有：

\[F^{d}(x)={(k_1,F(k_1)),k_2,F(k_2),…,(k_{n+1},F(n+1))} \]

\(F^{d}(x)\) 即为多项式 \(F(x)\) 的点值表达式。
（引用于我之前写的博客）

那么我们对 \(A(x),B(x)\) 分别求出其对应的点值表达，则 \(A*B \iff A^{d}(x)*B^{d}(x)\)。

进一步的可以简化计算，也就是我们对 \(A,B\) 取相同的“横坐标”，即集合 \({k_1,k_2,…,k_{2n+1}}\)，则可以得到：

\[A*B \iff A^{d}(x)*B^{d}(x)={(k_1,A(k_1)*b(k_1)),k_2,A(k_2)*B(k_2),…,(k_{2n+1},A(k_{2n+1})*B(k_{2n+1}))} \]

取 \(2n+1\) 个不同的点是因为两个 \(n\) 次的多项式相乘，最高次项有 \(2n\) 次，也就需要 \(2n+1\) 个点来表示。

• 对点值表示下多项式乘法，可以理解为画两个函数图像，对二图像上横坐标相同的点纵坐标相乘，显然得到的是卷积后的多项式所表示的函数。

接下来文章中出现的 \(n\) 默认为 \(2\) 的次幂。

step2：处理后事

问题来了，我们如何将多项式快速转化成点值表达，并且将点值表达转换回系数表达呢？

为了问题能快速解答，我们需要利用一组特殊的点，也就是 \(n\) 次单位根。（不知道的回去看博客）

严格意义上我们定义满足 \(x^n=1(x∈\text{C})\) 的 \(x\) 的解集为 \(\{\omega_{n}^k|k=0,1,2,..,n-1\}\)。

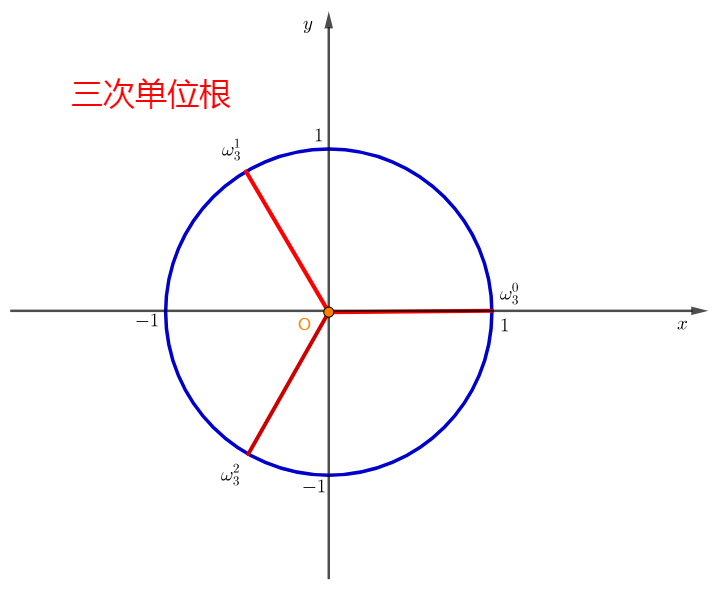
结合上面这张图简单加深下印象。

显然 \(n\) 次单位根就是从 \(x\) 轴（实轴）正半轴开始，将圆等分为 \(n\) 份。

简记 \(\omega_n^1\) 为 \(\omega_{n}\)，易得 \(\omega_{n}=\text{exp}\frac{2\pi i}{n}=(cos\big(\frac{2π}{n} \big),sin\big(\frac{2π}{n} \big))\)（据欧拉公式）。

• 单位根几个简单的性质：

1、\(\omega_n^0=1\)

2、\(\omega_n^k=\omega_n^{k\mod n}\)（周期性，显然）

3、\(\omega_n^{k+n/2}=-\omega_n^k\)（由三角表达式可以得到）

4、\(\omega_{2n}^{2k}=\omega_n^k\)

看起来这非常特殊，尤其是第四点，每次范围折半，可能可以分治！

step3：实践，DFT！

考虑将多项式 \(F(x)\) 转化为点值表达，带入的点值用单位根。

• 注意：多项式仅有 \(n-1\) 项，而不是 \(n\) 项，不然会少一个点而不能表达！具体操作的时候可以直接把 \(n\) 拓展到大于 \(n\) 的 \(2\) 的整数次幂。

我们考虑一种分治方式：

\[F(x)=(a_0+a_2x^2+…+a_{n-2}x^{n-2})+(a_1x^1+a_3x^3+…+a_{n-1}x^{n-1}) \]

设多项式 \(FL(x)\)、\(FR(x)\)：

\[FL(x)=a_0+a_2x+…+a_{n-2}x^{\frac{n}{2}-1} \]

\[FR(x)=a_1+a_3x+…+a_{n-1}x^{\frac{n}{2}-1} \]

则：

\[F(x)=FL(x^2)+xFR(x^2) \]

这样划分的方式使得分治时左右比较相似。接下来带入单位根并考虑性质：

当 \(k<\frac{n}{2}\)：

\[F(\omega_{n}^{k})=FL(\omega_{n}^{2k})+\omega_{n}^{k}FR(\omega_{n}^{2k}) \]

利用单位根性质得（\(n\) 为 \(2\) 的整数次幂）：

\[F(\omega_{n}^{k})=FL(\omega_{n/2}^{k})+\omega_{n}^{k}FR(\omega_{n/2}^{k}) \]

这样就满足分治的式子了，可以对 \(FL(x),FR(x)\) 分别计算。

当 \(k<frac{n}{2}\)，考虑 \(k+n/2\)：

\[F(\omega_{n}^{k+n/2})=FL(\omega_{n}^{2k+n})+\omega_{n}^{k+n/2}FR(\omega_{n}^{2k+n}) \]

利用性质 \(2,3,4\) 可以得到：

\[F(\omega_{n}^{k+n/2})=FL(\omega_{n/2}^{k})-\omega_{n}^{k}FR(\omega_{n/2}^{k}) \]

也满足分治的情况，分别计算。

归纳

设 \(k<n/2\)，则：

\[F(\omega_{n}^{k})=FL(\omega_{n/2}^{k})+\omega_{n}^{k}FR(\omega_{n/2}^{k}) \]

\[F(\omega_{n}^{k+n/2})=FL(\omega_{n/2}^{k})-\omega_{n}^{k}FR(\omega_{n/2}^{k}) \]

发现两个式子只差了一个 \(\omega_{n}^{k}\) 的符号，因此合并计算，且合并后即为原多项式的点值表达。

时间复杂度 \(O(n\text{ log }n)\)。

代码比较简单不放了，可以看原博客。

step4：更进一步，IDFT！

现在已知 \(A(k)=\displaystyle \sum_{i=0}^{n-1}a_i*(\omega_{n}^k)^i\)，求原多项式系数 \(a_i\)，可以比较简单的构造出矩阵：

\[\begin{equation} \begin{bmatrix} (\omega_n^0)^0 & (\omega_n^0)^1 & \cdots & (\omega_n^0)^{n-1} \\ (\omega_n^1)^0 & (\omega_n^1)^1 & \cdots & (\omega_n^1)^{n-1} \\ \vdots & \vdots & \ddots & \vdots \\ (\omega_n^{n-1})^0 & (\omega_n^{n-1})^1 & \cdots & (\omega_n^{n-1})^{n-1} \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ \vdots \\ a_{n-1} \end{bmatrix} = \begin{bmatrix} A(\omega_n^0) \\ A(\omega_n^1) \\ \vdots \\ A(\omega_n^{n-1}) \end{bmatrix} \end{equation} \]

根据单位根的对称性质不妨构造矩阵：

\[\begin{equation*} \mathbf D = \begin{bmatrix} (\omega_n^{-0})^0 & (\omega_n^{-0})^1 & \cdots & (\omega_n^{-0})^{n-1} \\ (\omega_n^{-1})^0 & (\omega_n^{-1})^1 & \cdots & (\omega_n^{-1})^{n-1} \\ \vdots & \vdots & \ddots & \vdots \\ (\omega_n^{-(n-1)})^0 & (\omega_n^{-(n-1)})^1 & \cdots & (\omega_n^{-(n-1)})^{n-1} \end{bmatrix} \end{equation*} \]

上面的系数矩阵记为 \(\mathbf V\)，则可以比较简单的证明：\(\frac{1}{n}\mathbf D = \mathbf V^{-1}\)。

则可以得到 \(IDFT\) 的式子其实就是 \(DFT\) 中单位根取相反数：

\[a_i=\frac{1}{n}\sum_{i=0}^{n-1}(\omega_{n}^{-k})^iA(i) \]

也就是做 \(DFT\) 的时候把 \(\omega_n^{k}\) 换成 \(\omega_n^{-k}\)。

更详细的证明可以看 OI Wiki，或者可以尝试用单位根反演证明（本质上就是反演）。

一些优化

递归版的 \(FFT\) 比较容易 \(TLE\)，空间占用也较大，可以考虑把递归改成循环实现。

考虑一开始按照奇偶性去分治的性质，可以理解为：

考虑对 \(A\) 做一次变换，将 \(A\) 变为 \(\{A_0, A_2, A_4, A_6, ...\}\), \(\{A_1, A_3, A_5, A_7, ...\}\)

观察二进制位，可以发现本质上是按第 \(1\) 位二进制位为关键字进行排序。

再变换一次，第一个序列变为 \(\{A_0, A_4, ...\}\), \(\{A_2, A_6, ...\}\) 观察二进制位，可以发现本质上是按第 \(2\) 位二进制位为关键字进行排序。

于是整个变换的过程，相当于我们分别以第 \(1\) 位二进制位、第 \(2\) 位二进制位、第 \(3\) 位二进制位……为关键字进行排序，也就是从低位到高位进行比较排序。可以注意到，这一方法和我们平时比较两个整数大小（从高位到低位比较）是相反的，所以整个变换相当于以二进制位翻转后的下标为关键字进行排序。

这也就是 \(FFT\) 蝴蝶变换，转化递归为循环迭代。

可以结合图理解下：

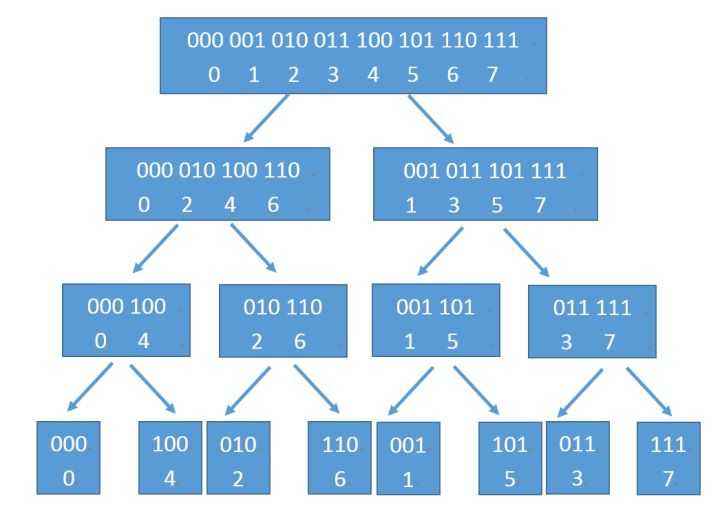
（图源网络）

实现

递归

(先占坑)

蝴蝶迭代

(先占坑)

再探 NTT

step1：寻找替身

当 \(FFT\) 拥有了模数，他就裂开了……因为复数域是不好取模的，所以考虑是否可以用一些特殊的整数代替。

设模数为 \(p\)，考虑模 \(p\) 意义一一组不同的整数可以代替单位根。我们希望这些数字都有共性，比如可以用一个底数表示，所以选择 数论原根。

原根具体的定义可以看之前那篇博客：

称 \(g\) 为模 \(p\) 的原根，当且仅当 \(\{g^0,g^1,…,g^{p-2}\}\) 在模 \(p\) 的意义下互不相同。

注意到之前所用的 \(n\) 为 \(2\) 的整数次幂，则需要尽量选择 \(p=a*2^k+1\) 这一形式的质数；换言之，也就是 \(n\mid p-1\)。

则可以令 \(\omega_{n}^{1}\equiv g^{\frac{p-1}{n}}\pmod p\)，显然根据原根的定义，\(g^{\frac{p-1}{n}*k}(k=0,1,..,n-1)\) 在模 \(p\) 意义下互不相同。

显然是与我们所要的单位根性质所一致的，并且仍有类似单位根的递推性质和对称性。

step2：替换，实现！

考虑多项式 \(A(x)\)，在原根下的点值表达（\(DFT\)）：

\[A(k)=\sum_{i=0}^{n-1}a_i(g^{\frac{p-1}{n}})^k \]

反演（\(IDFT\)）：

\[a_k=\frac{1}{n}\sum_{i=0}^{n-1}A(i)(g^{-\frac{p-1}{n}})^k \]

然后同样做 \(FFT\) 即可。