网络流详解-算法与优化

前言

我经常听别人说网络流很难、建图学不会之类的话，所以很多人都比较晚学习网络流。

但是你别看网络流这个高端的名词，也不过就那样。学习总是不能害怕的，迎难而上才是硬道理。

本文希望能帮助更多的人弄懂网络流，也希望大家再也不会“望网络流而生畏”。

请你一定要相信：任何时候，任何事，总会有最优的解决办法！

我特地将网络流拆成几篇来写，这一篇主要讲解算法，后面将会介绍一些定理和应用。

注：下文用 \(n\) 代表点数，\(m\) 代表边数。

引入

如果提到“流”你会想到什么？最简单的就是水流了。所以很多人用水流来抽象网络流的过程。

现在有一张有向无环图，\(S\) 点是自来水厂，\(T\) 点是废水厂，每条边都有一个容量，超过了容量水就会溢出。换句话说，每条边最多有一定量的水流过。从 \(S\) 点放出足量的水，现在请你求 \(T\) 点最多有多少流量。（流量就定义为水量）

仔细想想觉得很简单？只要找到每条路径中对整条路径水量限制的路径就好了，也就是一条路径中容量最小的边。但是你是否考虑过“分流”的问题呢？你可以把分流理解为水流到了“岔路口”，当然爆搜是可以的。但是如果点数很大呢？

如果你没看懂上面再说什么，那么来看看下面这个实例：

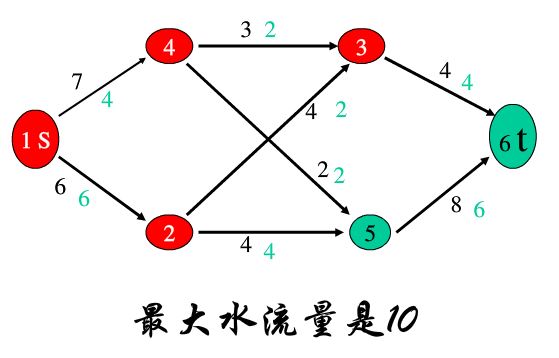
（图源网络，侵删）

我们需要一个改进的算法了。

定义

现在开始就是正式地介绍网络流了，下面会先介绍一些在网络流中的定义。

• 源点（\(S\)），从字面来看是“流出的来源”，你可以把它理解为自来水厂；

• 汇点（\(T\)），即所有水流汇聚的地方，你可以把它理解为废水厂；

• 容量，图中的每一条边都有一个非负容量，你可以理解为这条边最多流过的水量；

上面这整张图就称为“网络流图”，也就是整个水流图。

• 可行流：对于源点，流出的（水）量为整张图的流量（不浪费的情况下，也就是水不能溢出）；对于汇点，流入的（水）量为整张图的流量。注意每个节点是不能储水的！对于中间的其他点，流入的量会等于流出的量（因为不能储水，不然往哪放啊）。满足这样条件的水流就是一个可行流。

可行，也就是可以这样流。就相当于在 \(S\) 点时选择一个不会浪费的水量放出。当然一般情况下我们都要求最大流。

先别管最大流是啥了，上面的看懂了吗？注意容量和流量两个东西的区别哦！

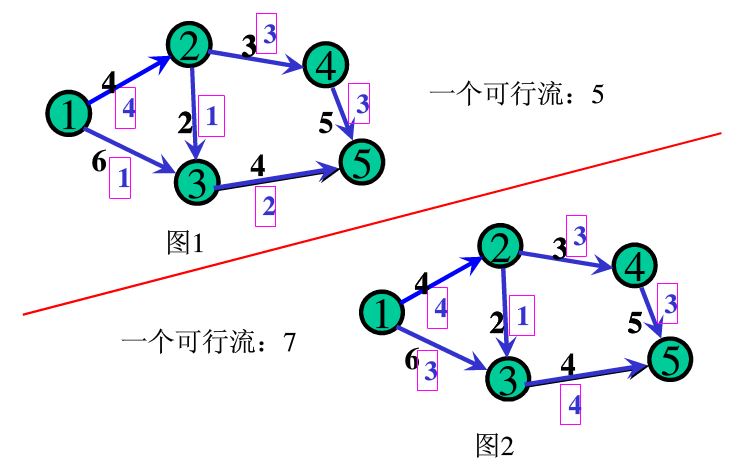
（图源网络，侵删）

其中注意黑色的是容量，方框里的是流量。

• 最大流：在所有可行流中流量最大的一个可行流。这个应该比较好理解。上图中的最大流是多少呢？就是 \(7\)。

注意：最大流的方案可能不止一个！因此题目如果让你输出路径，一般会有 \(SPJ\)。

下面我们将会讲解求最大流的几种算法。

EK 算法

算法思想

这个算法背景就不介绍了，虽然比较慢，但是也很简单。

• 增广路：即一条 \(S\) 到 \(T\) 的路，一定水流流过了这条路可以使流量增加。（注意这条路不能“满流”，不然水就流不过去了）

一开始流量是 \(0\)，我们只需要一直找增广路以增加流量，直到图中不存在增广路（原先的增广路全部满流），这样图中的流就是最大流。这个根据上面的定义应该比较好理解吧。

解释：因为流过增广路可以使流量增加，因此不存在增广路时流量就不能增加了，因此对应了最大流量。

具体操作的时候也比较简单，我们可以一直进行 \(bfs\)（拓展宽度较快，找增广路比较优，\(dfs\) 也可），一直走正边权（容量）的边。然后找到增广路时，限制整条路的流量就是增广里中容量最小的边，把整条路的容量减去这个值。因为每次都会减掉一些已经流过的流量，这样也就能“删除”增广路，也是上面找“正边权”的边的原因。（因为会有 \(0\) 边权）

看着很简单，随便模拟一下就好了。这样就求完最大流了？并不是！

要不然为啥这么多年了最大流算法那么少呢……

考虑一个问题：万一你拓展的增广路不是最优的，后面其实还有更优的路径，但是你流错地方了……

这样就会出错，为什么还会流错呢？准确来讲不是流错，而是不是最优。这样如果图比较大，那么就可能出错。

还是这张图，如果选取 \(S=1,T=5\)，选择 \((1,2,3,5)\) 这条路增广可以增加 \(2\) 的流量；而选取 \((1,3,5)\) 却可以增加 \(4\) 的流量；前面一种方案显然不会更优，甚至有可能切断其他更优的边。你可能会认为后面继续增广的时候会把流量调到正确对吧？这也是我一开始有的疑虑。下面再引入一张图：

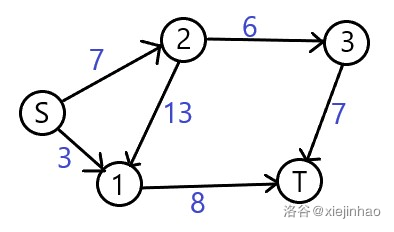
（图为本人原创，若要转载请注明出处）

别看这张图简单，但是其中大有玄妙。这其中选择增广路大有学问：

1、按照 \(bfs\) 序，可能会选择 \((S,2,1,T)\)，显然 \((S,2)\) 这条边满流了，整条路的流量为 \(7\)，然后 \((S,2)\) 就被切断了；然后还会找到 \((S,1,T)\) 这条路，因为刚刚 \((1,T)\) 流过了 \(7\) 的流量，因此此时 \((1,T)\) 仅剩 \(1\) 容量，所以可以增加 \(1\) 的流量。这样计算出来的整张图的最大流是 \(8\)；

2、更优的路径：\((S,2,3,T)\)，流过 \(6\)；\((S,2,1,T)\)，流过 \(1\)（\(S,2\) 仅剩 \(1\) 容量）；\((S,1,T)\) 流过 \(3\)；总容量 \(10\)。

是不是发现直接找增广路会出错了？这张图的最大流就是 \(10\)。

怎么解决问题呢？现在就要讲解最难懂的思想了：反向边。

简单来讲，这条边是用来撤销之前的操作的。（留条后路）一开始反向边的边权是 \(0\)。

在找到一条增广路后，我们会对这条增广路的边权操作一下（减去增加的流量），然后我们要在反向边上加上增加的流量。

让我们看看这样会发生什么？以上面的图为例，选择了 \((S,2,1,T)\)，并且添加反向边（边权为 \(0\)）的未画出：

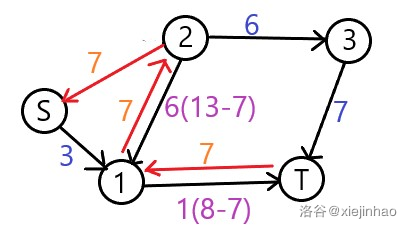
（图为本人原创，如需转载请注明出处）

然后继续找增广路，会走过 \((1,2)\) 一条反向边，走 \((S,1,2,3,T)\)，增加 \(3\) 的流量；或者走 \((S,1,T)\) 增加 \(1\)，再走 \((S,1,2,3,T)\) 增加 \(2\)；反正就是会增加 \(3\) 的流量。然后加上面所计算的 \(7\)，答案为 \(10\)，正确！

为什么反向边有这个作用？你有没有发现，在选择了 \((S,2,1,T)\) 之后，添加反向边就像是给 \((S,1)\) 这条边留了“后路”；在走 \((S,1)\) 这条边的时候，会把原本属于这条边的流量通过 \((1,2)\) 这条反向边走出去，就像是撤销了之前的操作！感觉操作了一次还留了后路，真香！

为什么这样是正确的？你可以理解为：一开始是“尝试性”去找增广路，有可能有些流量需要“调整”，反向边起到了这个调整的作用。为了大家感性理解，这里不讲冗长的证明，你只需理解上面的图和下面一小段文字解释就可以了。

不知道这里大家看不看得懂反向边这一波优秀的操作呢？如果大家有兴趣可以去看看严谨的证明。

思路总结和性能分析

所以我们得到了一个正确的算法：

1、找增广路，并给整条路减去增加的流量，答案累加上增加的流量；

2、给反向边加上流量用来撤回；

3、重复 1、2 两步直到不存在增广路，此时的答案就是整张图的最大流。

感觉简单极了！一开始自来水场的问题也可以解决了。但是这个算法的时间复杂度呢？

我们分析一下：最坏的情况下，每次增广都只能增广一条边，因此需要 \(m-1\) 次；\(bfs\) 时存在反向边，因此最坏情况下要 \(n*m\) 次遍历整张图，所以总的时间复杂度是 \(O(NM^2)\)。但是我们都说了是一般情况，因此随机情况下这个是远远达不到上界的，还是可以放心使用（当然出题人也可能卡）。

模板题：网络最大流 （因为模板到处都是我就拿洛谷的了）

代码

回顾上面的思路，我们可以得出下面的代码：

#include<bits/stdc++.h>
using namespace std;

const int inf = 1 << 29;
const int N = 1e4 + 10;
const int M = 2e5 + 10;

int head[N], edge[M], ver[M], Next[M], tot;
void add(int x, int y, int v) {
	ver[++tot] = y, edge[tot] = v, Next[tot] = head[x], head[x] = tot;
	ver[++tot] = x, edge[tot] = 0, Next[tot] = head[y], head[y] = tot;
} 
// 一开始建正边的时候顺便建反边，注意初始反边权值为 0 
// 注意：tot 从 1 开始 接下来就是 正反对应 (2,3), (3,4) 
// 正边 x1 与反边 x2 的关系是 x1 ^ 1 = x2 , x2 ^ 1 = x1 
// 注意正反是相对的，反边的反边就是正边（负负得正） 
// 你需要把正边理解成 原来存在的边 

int pre[N], incf[N], n, m, s, t;
bool vis[N];
bool bfs() { // 找增广路 
	memset(vis, 0, sizeof vis);
	queue<int> q;
	q.push(s), vis[s] = 1;
	incf[s] = inf;
	while(q.size()) {
		int x = q.front(); q.pop();
		for(int i = head[x]; i; i = Next[i]) 
			if(edge[i] and !vis[ver[i]]) {
				int y = ver[i], val = edge[i];
				incf[y] = min(incf[x], val); 
				// incf 记录增广路上最小边容量 
				pre[y] = i, q.push(y), vis[y] = 1;
				// pre 数组记录转移路径，增广完之后要更新边权 
				if(y == t) return 1; // 有一条路增广到汇点就可以 
			}		
	}
	return 0; // 增广不到汇点，因此不存在增广路了 
}

int maxflow = 0;
void update() { // 更新边权 
	int x = t;
	while(x != s) {
		int i = pre[x];
		edge[i] -= incf[t];
		edge[i ^ 1] += incf[t];
		x = ver[i ^ 1];
	}
	maxflow += incf[t]; 
}

int main() {
	tot = 1;
	scanf("%d %d %d %d", &n, &m, &s, &t);
	for(int i = 1, x, y, V; i <= m; i++) {
		scanf("%d %d %d", &x, &y, &V);
		add(x, y, V);
	} // 建图 比较简单 
	while(bfs()) update(); 
	// 1. 找增广路(bfs) 
	// 2. 正边减去增加流量，反边加上(update)
	// 3. while 重复 1、2，直到不存在增广路退出 
	printf("%d\n", maxflow);
	return 0;
}

注意上面用了一个小技巧，就是正边与反边的关系只需要异或上 \(1\)，这个是可以记住的。

（反正可以过模板就对了）

但是你会发现这个算法真的不是很优秀啊……因为每次只能增广一条路，要是能多条路增广呢？

dinic 算法

算法思路

• 残量网络：在增广后剩余流量组成的网络。（你就顾名思义吧，不要那么复杂）

其实我们上面的 \(EK\) 算法已经讲清楚了这个算法的步骤，不过它找增广路的效率实在是太低了！

考虑刚才进行的 \(bfs\)，它找到了一条 \(S-T\) 的“最短路径”，但是确实整个最短路图上的一条链而已！

我们干脆对整张图进行“分层”，上一层节点可以到达下一层节点，然后统一增广，可以证明这样找增广路的效率最高。

具体分层就是下一层的编号等于上一层的编号加一，反正模拟起来挺简单的。但是我们不是要增广嘛？分层完了有啥用啊！

别急，这次我们可以直接 \(dfs\) 增广，具体看下面的代码：

bool bfs() { // d 数组是分层的数组
	memset(d, 0, sizeof(d));
	queue<int> q;
	q.push(s), d[s] = 1;
	while(q.size()) {
		int x = q.front(); q.pop();
		for(int i = head[x]; i; i = Next[i]) 
			if(v[i] && !d[ver[i]]) {
				q.push(e[i]);
				d[ver[i]] = d[x] + 1;
				if(ver[i] == t) return 1;
			}
	}
	return 0;
}

int dinic(int x, int flow) { // flow 当前流量
	if(x == t) return flow;
	int rest = flow, k; // rest 剩余流量
	for(int i = head[x]; i && rest; i = Next[i]) 
		if(edge[i] && d[ver[i]] == d[x] + 1) { 
			// 这条边在分层的图上 注意要有容量才增广 
			k = dinic(ver[i], min(rest, edge[i]));
			if(k == 0) d[ver[i]] = 0; 
			// 小优化：一个点内子树流量为 0，后面就不用再遍历了
			// 因为无论如何遍历都是 0 
			edge[i] -= k, edge[i ^ 1] += k;
			rest -= k; // 更新流量 
		}	
	return flow - rest;
}

现在就体现出分层图的作用了吧！（变量名和模板题都是一样的）

当然此“分层图”非彼“分层图”（算了你都绕晕了），后面我还会提到。

当前弧优化

原理：用一个数组 \(cur\) 代替 \(head\) 进行增广。

\(cur\) 数组是什么呢？考虑一个节点 \(x\)，他有很多儿子（指分完层的图上的），干脆从 \(1-k\) 编号吧；那假设我们把它 \(1,2,3\) 儿子的流量都用完了，也就是它到儿子 \(1,2,3\) 的边已经没有容量（满流），那么我们下次增广从 \(4\) 开始就好了，没有必要在 \(1-3\) 上浪费时间。这也就是 \(cur\) 数组的正确性。

以上的这个优化就叫做当前弧优化。其实图论中，特别是网络，弧就相当于边。反正你好理解就行。

具体实现的时候，因为 \(bfs\) 分层还要用到原来的数组 \(head\)，因此在增广前先把 \(head\) 复制一份给 \(cur\)，然后用 \(cur\) 增广；增广的时候，更新 \(cur\)，\(cur_x\) 表示当前节点遍历到哪条边了，具体的修改就是这样的：

int dfs(int x, int flow) {
	if(x == t) return flow;
	int rest = flow, k;
	for(int i = cur[x]; i && rest; i = Next[i]) {
		cur[x] = i; // 更新当前点到哪儿了 
		if(edge[i] && d[ver[i]] == d[x] + 1) { 
			// 这条边在分层的图上 注意要有容量才增广 
			k = dfs(ver[i], min(rest, edge[i]));
			if(k == 0) d[ver[i]] = 0; 
			// 小优化：一个点内子树流量为 0，后面就不用再遍历了
			// 因为无论如何遍历都是 0 
			edge[i] -= k, edge[i ^ 1] += k;
			rest -= k; // 更新流量 
		}	
	}		
	return flow - rest;
}

int dinic() {
	int maxflow = 0, flow;
	while(bfs()) {
		for(int i = 1; i <= N; i++)
			cur[i] = head[i]; // N 最大点数
		// 具体就是复制，实在不行就 memcpy
		while((flow = dfs(s, inf))) 
			maxflow += flow; 
	} return maxflow;
}

这次我给出了更新最大流的代码（最后一段），即使是原先没有优化的 \(dinic\) 也是这样更新，\(inf\) 需要赋一个恰当的值，不要爆 \(\text{int}\) 或者 \(\text{long long}\) 了。（\(bfs\) 部分是一样的）

性能分析

先分析 \(dfs\)：修改增广路上边的流量。至多会增广 \(m\) 次，一条增广路的长度至多是 \(n\)，所以这一部分的复杂度是 \(O(nm)\)。dfs遍历时找增广路失败时经过的边。由于一旦从某条边出发找最短路失败了，我们就不会再走那条边（这个情况是当前弧优化的），所以这一部分的复杂度是 \(O(m)\) 的。故而dfs增广的复杂度是 \(O(nm)\)。

再分析 \(bfs\)：每次 \(dfs\) 增广后我们都会重新 \(bfs\) 分层整张图，因此残余网络上 \(S\) 到 \(T\) 的最短路长度一定不会减少，所以至多重建 \(n-1\) 次图。当 \(n,m\) 同阶，可以认为这一部分时间复杂度是 \(O(n)\)。

因此 \(dinic\) 的时间复杂度上界 是 \(O(n^2m)\)，会比 \(EK\) 好些。

但是注意：网络流除非出题人可以卡，否则时间复杂度都是远远达不到上界的！

但是现在出题人都有共识吧……非特殊情况绝对不卡 \(dinic\)。

（以上内容一部分改编自网络，侵删）

完整代码

还是以模板为例，为了防止你再向上翻，所以再给一次连接：网络最大流

#include<bits/stdc++.h>
using namespace std;

const int inf = 1 << 29;
const int N = 1e4 + 10;
const int M = 2e5 + 10;

int head[N], edge[M], ver[M], Next[M], tot;
void add(int x, int y, int v) {
	ver[++tot] = y, edge[tot] = v, Next[tot] = head[x], head[x] = tot;
	ver[++tot] = x, edge[tot] = 0, Next[tot] = head[y], head[y] = tot;
}

int d[N], cur[N], n, m, s, t, maxflow;

bool bfs() {
	memset(d, 0, sizeof(d)), d[s] = 1;
	queue<int> q; q.push(s);
	while(q.size()) {
		int x = q.front(); q.pop();
		for(int i = head[x]; i; i = Next[i]) 
			if(edge[i] && !d[ver[i]]) {
				q.push(ver[i]);
				d[ver[i]] = d[x] + 1;
				if(ver[i] == t) return 1;
			}
	}
	return 0;
}

int dinic(int x, int flow) {
	if(x == t) return flow;
	int rest = flow, k;
	for(int i = cur[x]; i && rest; i = Next[i]) {
        cur[x] = i;
        if(edge[i] && d[ver[i]] == d[x] + 1) {
			k = dinic(ver[i], min(rest, edge[i]));
			if(k == 0) d[ver[i]] = 0;
			edge[i] -= k, edge[i ^ 1] += k;
            rest -= k;
		}	
    }
		
	return flow - rest;
}

int main() {
	tot = 1;
	scanf("%d %d %d %d", &n, &m, &s, &t);
	for(int i = 1, x, y, V; i <= m; i++) {
		scanf("%d %d %d", &x, &y, &V);
		add(x, y, V);
	}
	
	int flow = 0;
	while(bfs()) {
        for(int i = 1; i <= n; i++)
            cur[i] = head[i];
        while((flow = dinic(s, inf)))
			maxflow += flow;
    }
		
	printf("%d\n", maxflow);
	return 0;
}

是不是感觉很简单啊

好吧请你过下这一题：网络最大流（加强版）

我：\(T\) 飞了。

大佬：我用 \(dinic\) * 过去啦！

我：……

好吧你还是很强，这里 \(dinic\) 的做法还是不谈了，因为已经可以卡到 \(T\) 了。

再次考虑有没有其他更好的算法……

当然你可能听别人说过 \(\text{SAP}\) 和 \(\text{ISAP}\)，但是前者的时间复杂度上界为 \(O(NM^2)\)，后者为 \(O(N^2M)\)，可以说也是没有办法通过这种毒瘤题的……（不然为何叫加强版）所以，换个思路试试？

预流推进-最高标号法

其实这个算法就像是暴力的思路。一开始碰到这种题目，不会网络流，就想：能不能一条路一条路把流量推出去，但是后面感觉不可做。但是确实有大佬发明出了这种东西……说不定你在想暴力的时候多钻研一下，就能自己 \(yy\) 出预留推进了呢（雾

其实最高标号预流推进你可以叫它 \(\text{HLPP}\)。

（其实预流推进也有很多种

（但是还是写 \(\text{HLPP}\) 好点

算法思想

还记得我们一开始说的水的问题嘛？我们可以让源点流出 \(inf\) 的水，即使把水管撑爆了也不要紧，反正最后到达 \(T\) 的就那么多。你可能一开始想的暴力就是这样的吧！但是你很快发现你打完之后竟然是错的，或者 \(T\) 到飞起。

为了防止出现 \(\text{TLE}\) 的情况，也就是出现两个节点，因为没有确定顺序推来推去……所以我们给每个节点确定一个高度 \(h\)，就像现实中的水流一样从高向低流。特别的，源点的高度为 \(n\)，其他点高度都可以为 \(0\)。

因为我们一开始放出了 \(inf\) 的流量，导致每个节点会流很多超过能流出的流量（当然流入还是要按照容量限制流入），我们规定一个节点可以暂时储存流量，超出的流量暂且叫它“超额流”。我们只需要把这些超额流每次推出去就好了。当遇到一个点周围所有的点高度都大于它时，我们就抬高它的高度。抬高到什么高度呢？其实我们只要恰好让它流出去就行，所以抬高到它周围高度最小的节点的高度 \(+1\) 就行。

对于 \(x\) 节点每次流出时，假设可以留到 \(y\)，当且仅当 \(h_x=h_y+1\)。为什么是等于？因为跟据我们每次抬高的性质，也是为了后面的一个小小优化。（注意要有 \(x\) 到 \(y\) 的有容量的边才行哦）每次能流出的超额流量就是 \((x,y)\) 的容量与超额流量两者的最小值。

接下来用 \(rest\) 数组表示一个节点的超额流量。\(\text{Tarjan}\) 发现每次取出高度最高的节点进行推进（也就是推出超额流）操作，时间复杂度最小。为什么呢？你可以理解成高度高的先给了低的，然和低会把这些流传给更低的，显然会少遍历一些遍历过的节点。这个可以使用优先队列维护，只要一个节点超额流不为 \(0\)，扔进去就好了。

注意：每一次推进我们都尽量推出多的超额流；特别的，如果一个节点高度抬高到超过了 \(S\) 的高度，则这个多的流会被退回给 \(S\)，所以这样的正确性是可以保证的。

然后还是考虑下一开始设的操作，我们发现除了源点外其他点高度都为 \(0\) 会很浪费时间——因为要抬高很多次。所以我们干脆从 \(T\) 开始 \(bfs\)，像 \(dinic\) 那样分层设置高度就可以了。（从 \(T\) 开始是因为 \(T\) 的高度最小）

下面是推进操作和抬高操作的代码：

void push(int x) { // 推进操作 
	for(int i = head[x], y; i and rest[x]; i = Next[i]) {
		if(x != s and h[y = ver[i]] + 1 != h[x]) continue;
		if(!edge[i]) continue;
		// 1.非源点或高度不满足限制，不能走
		// 2.这条边没有容量了，不能走 
		int flow = min(rest[x], edge[i]);
		rest[x] -= flow, rest[y] += flow;
		edge[i] -= flow, edge[i ^ 1] += flow;
		// 反向边还是要有的（万一推错了呢） 
		if(y != s and y != t and !v[y]) 
			q.push(make_pair(h[y], y)), v[y] = 1; 
		// v 1/0 数组代表一个节点 是/否 在队列中 
	}
}

void update(int x) { // 更新高度 
	h[x] = inf;
	for(int i = head[x]; i; i = Next[i]) 
		if(edge[i] and h[ver[i]] + 1 < h[x])
			h[x] = h[ver[i]] + 1;
}

\(q\) 是 \(STL\) 实现的优先队列，内容为 \(pair\)，第一关键字是高度，第二关键字是编号。

整体感觉实现起来很简单？具体代码就是那样了，也不给出了，因为可能跑的很慢过不了这题……

总结来说：

1、从 \(T\) 开始 \(bfs\)， 给每个点分层，设置初始高度，然后 \(h_s=n\)并把 \(S\) 放入队列；

2、推进（上面的 \(push\) 函数），每次取出高度最高的节点；

3、若一个节点的高度比他周围节点低，则抬高这个节点的高度至它周围节点的最低高度 \(+1\)；

4、重复步骤 \(2,3\) 直至队列为空，此时汇点的超额流就是整张图的最大流。

正确性显然吧！注意如果一个节点的超额流为 \(0\) 则不用入队哦！每个节点都恰好没有超额的流量，所有流量要么退回给 \(S\)（不得已的情况，即汇点已满），要么给了汇点，所以是正确的！

gap 优化

故名思意，“断层优化”。为什么“断层”？……

好吧其实这个优化比较简单，就是说：如果一个高度 \(h'\) 不存在，那么所有高度比 \(h'\) 高的点都不能到达汇点 \(T\)，为什么呢？想想上面的推进代码，必须要两点之间高度严格差 \(1\)，如果有一个高度不存在，那么比这个高度高的点就断开了，没有办法下传，因此这样是对的。

事实证明这个优化挺有用的，起码比上面的朴素实现快了很多！(虽然我没试过)

代码

注：这份代码是有 \(gap\) 优化的，没有 \(gap\) 优化的情况可以直接把和 \(gap\) 有关部分去掉。

还是再放上题目链接：网络最大流（加强版）

#include<bits/stdc++.h>
#define inf (1LL << 60)
using namespace std;

const int N = 1.2e3 + 10;
const int M = 2.4e5 + 10;

int head[N], ver[M], Next[M], cnt = 1;
long long edge[M];

void add(int x, int y, int v) {
	ver[++cnt] = y, edge[cnt] = v;
	Next[cnt] = head[x], head[x] = cnt;
	
	ver[++cnt] = x, edge[cnt] = 0;
	Next[cnt] = head[y], head[y] = cnt;
}

int h[N], gap[N * 2], n, m, s, t; 

bool bfs() {
	memset(h, 0x3f, sizeof h), h[t] = 0;
	queue<int> q; q.push(t);
	while(q.size()) {
		int x = q.front(); q.pop();
		for(int i = head[x]; i; i = Next[i]) 
			if(edge[i ^ 1] and h[ver[i]] > h[x] + 1) {
				h[ver[i]] = h[x] + 1;
				q.push(ver[i]);
			}
	}
	return h[s] != 0x3f3f3f3f;
}

priority_queue< pair<int, int> > q;
long long rest[N]; bool v[N];

void push(int x) { 
	for(int i = head[x], y; i and rest[x]; i = Next[i]) {
		if(h[x] != h[y = ver[i]] + 1 and x != s) continue;
		if(!edge[i]) continue;
		int flow = min(rest[x], edge[i]);
		rest[x] -= flow, rest[y] += flow;
		edge[i] -= flow, edge[i ^ 1] += flow;
		if(y != s and y != t and !v[y]) 
			q.push(make_pair(h[y], y)), v[y] = 1;  
	}
}

void update(int x) { 
	h[x] = 1 << 30;
	for(int i = head[x]; i; i = Next[i]) 
		if(edge[i] and h[ver[i]] + 1 < h[x])
			h[x] = h[ver[i]] + 1;
}

void Gap(int x) { 
	for(int i = 1; i <= n; i++)
		if(i != s and i != t and h[i] > h[x] and h[i] < n + 1)
			h[i] = n + 1;
}

long long HLPP() {
	if(!bfs()) return 0; // 无解
	h[s] = n, rest[s] = inf, push(s);
	// 可以先推进 s，因为 s 推出了无穷的流量
	// 这就意味着 s 的流量推不完的 所以先推
	// 即使 s 还有多也不要紧 
	for(int i = 1; i <= n;  i++)
		if(h[i] <= n) gap[h[i]]++;
	while(q.size()) { 
		int x = q.top().second; 
		q.pop(), v[x] = 0, push(x);
		if(rest[x]) { // 还有剩余无法流出 需要抬高 
			if(!--gap[h[x]]) Gap(x); // gap 优化 
			update(x), gap[h[x]]++, v[x] = 1;
			q.push(make_pair(h[x], x));
		}
	}
	return rest[t];
}

int main() {
	scanf("%d %d %d %d", &n, &m, &s, &t);
	for(int i = 1, x, y, v; i <= m; i++) {
		scanf("%d %d %d", &x, &y, &v);
		add(x, y, v);
	} 
	printf("%lld\n", HLPP());
	return 0;
}

彩蛋

当然加个快读可能更快……还有一个优化叫做全局重贴标签，也就是边推进边抬高高度，听说很快？

反正这也就够了，起码模板题跑的效果还不错。

但是我不得不说很多人写的 \(hlpp\) 是有问题的，所以才会导致没优化常数或没采取其他优化方式过不了……

甚至还有更离谱的，普通模板跑的比 \(EK\) 都慢……大家写代码要认真点啊！

当然还有很多奇淫技巧优化的，可以看看花姐写的（除了码风不是那么优秀其他都很好啊）

链接给上：%%%花姐

当然 \(dinic\) 混过去的代码怎么能没有呢！看这

虽然说被 \(hack\) 了，但是怎么还能过呢……

后记

完结撒花！