【LGR-109】洛谷 5 月月赛 II & Windy Round 6
排名
(见证历史)
A P8344 「Wdoi-6」走在夜晚的莲台野
显然有解要满足 \(x \leq z\) 否则无解.
再考虑最多有多少个银色木板能被放入:
显然我们一定要先放银色, 再放金色(否则先放的金色会被浪费, 没有利用).
于是我们可以贪心地每次都放满银色, 再预留一个位置给即将放的金色. 具体地:
第 \(1\) 次操作: 可以放入 \(z - 1\) 个银色, 再放入一个金色, 取出 \(z - 1\) 个银色 (最后 \(1\) 个位置留给金色)
第 \(2\) 次操作: 可以放入 \(z - 2\) 个银色, 再放入一个金色, 取出 \(z - 2\) 个银色 (前面已经有了 \(1\) 个金色, 再预留 \(1\) 个位置)
第 \(3\) 次操作: 可以放入 \(z - 3\) 个银色, 再放入一个金色, 取出 \(z - 3\) 个银色 (前面已经有了 \(2\) 个金色, 再预留 \(1\) 个位置)
......
第 \(x\) 次操作: 可以放入 \(z - x\) 个银色, 再放入一个金色, 取出 \(z - x\) 个银色 (前面已经有了 \(z - x - 1\) 个金色, 再预留 \(1\) 个位置)
最后一个操作后还剩下 \(z - x\) 个位置, 此时金色已经用完, 可以全部放银色.
故对于 \(y\) 需要满足 \(y \leq (z - 1) + (z - 2) + .. + (z - x) + (z - x)\)
即 \(y \leq \frac{(2z - x - 1)x}{2} + z - x\) (等差数列求和都会吧)
注意 \(1 \leq y \leq 5 \times 10^{17}\) , 所以要开 long long.
时间复杂度: \(O(1)\)
#include <bits/stdc++.h>
#define int long long
using namespace std;
inline int read() {
int x = 0; char c = getchar(); bool f = 1;
while(c < '0' || c > '9') { if(c == '-') f = 0; c = getchar(); }
while(c >= '0' && c <= '9') { x = x * 10 + c - '0'; c = getchar(); }
return (f ? x : -x);
}
int t, x, y, z;
signed main() {
t = read();
while(t--) {
x = read(); y = read(); z = read();
if(x <= z && y <= (2 * z - x - 1) * x / 2 + z - x) puts("Renko");
else puts("Merry");
}
return 0;
}
B P8345 「Wdoi-6」华胥之梦
假设当前我们第 \(i\) 个走过的点为 \(p_i\) 那么据题意, 有:
\(length = \sum _{i = 1} ^{|s| - 1} (a[p_i] - 2a[p_{i + 1}] + c)\)
\(\ \ \ \ \ \ \ \ \ \ \ = (|s| - 1)c + \sum _{i = 1} ^{|s - 1|} a[p_i] - 2 \sum _{i = 1} ^{|s - 1|} a[p_{i + 1}]\)
\(\ \ \ \ \ \ \ \ \ \ \ = (|s| - 1)c + \sum _{i = 1} ^{|s - 1|} a[p_i] - 2 \sum _{i = 2} ^{|s|} a[p_{i}]\)
\(\ \ \ \ \ \ \ \ \ \ \ = (|s| - 1)c + (\sum _{i = 2} ^{|s - 1|} a[p_i] + a[p_i]) - (2 \sum _{i = 2} ^{|s - 1|} a[p_{i}] + 2a[p_{|s|}])\)
\(\ \ \ \ \ \ \ \ \ \ \ = (|s| - 1)c + a[p_i] - 2a[p_{|s|}] + \sum _{i = 2} ^{|s - 1|} a[p_i] - 2 \sum _{i = 2} ^{|s - 1|} a[p_{i}]\)
\(\ \ \ \ \ \ \ \ \ \ \ = (|s| - 1)c + a[p_i] - 2a[p_{|s|}] - \sum _{i = 2} ^{|s - 1|} a[p_i]\)
\(\ \ \ \ \ \ \ \ \ \ \ = (|s| - 1)c + 2a[p_i] - a[p_{|s|}] - \sum _{i = 1} ^{|s|} a[p_i]\)
推到这里, 我们发现, 要使 \(length\) 最小, 只需要使 \(a[p_i]\) 最小, \(2a[p_{|s|}]\) 最大即可.
注意, 最终结果有可能爆 int , 保险起见要开 long long .
剩下的套公式就好了:
时间复杂度: \(O(n)\)
#include <bits/stdc++.h>
using namespace std;
inline int read() {
int x = 0; char c = getchar(); bool f = 1;
while(c < '0' || c > '9') { if(c == '-') f = 0; c = getchar(); }
while(c >= '0' && c <= '9') { x = x * 10 + c - '0'; c = getchar(); }
return (f ? x : -x);
}
const int N = 1e6 + 10;
int n, c, q, l, minv, maxv, a[N], s[N];
long long sum;
inline bool cmp(int &x, int &y) { return a[x] < a[y]; }
int main() {
n = read(); c = read(); q = read();
for(int i = 1; i <= n; ++i) a[i] = read();
while(q--) {
l = read();
sum = 0; minv = 0x3f3f3f3f; maxv = -0x3f3f3f3f;
for(int i = 1; i <= l; ++i) { s[i] = read(); sum += a[s[i]]; minv = min(minv, a[s[i]]); maxv = max(maxv, a[s[i]]); }
printf("%lld\n", ((long long)l - 1) * c + 2 * minv - maxv - sum);
}
return 0;
}
C P8346 「Wdoi-6」最澄澈的空与海
显然有一个结论: 如果一个点只有一条边与之相连, 那么它只能和这条边上另一点相连.
于是我们可以循环找这样的点, 然后让它与这条边上另一点配对.
还有一种情况就是, 虽然这个点有很多边, 但是其它的都已经配对过, 只剩下一个点没有配对, 那么也可以直接相连.
最后看所有点是否配对即可.
个人认为这题甚至比上一题简单.
时间复杂度: \(O(n^2)\) (复杂度好像不太对, 但是能过)
#include <bits/stdc++.h>
using namespace std;
inline int read() {
int x = 0; char c = getchar(); bool f = 1;
while(c < '0' || c > '9') { if(c == '-') f = 0; c = getchar(); }
while(c >= '0' && c <= '9') { x = x * 10 + c - '0'; c = getchar(); }
return (f ? x : -x);
}
const int N = 1e7 + 10;
int t, n, m, u, v, res, tmp;//res:目前配对个数 tmp:上一次配对个数
bool vis[N];//vis[i]:i是否配对
int main() {
t = read();
while(t--) {
n = read(); m = read();
res = 0;
vector<int> mp[N];
for(int i = 1; i <= (n << 1); ++i) vis[i] = 0;
for(int i = 1; i <= m; ++i) {
u = read(); v = read() + n;
mp[u].push_back(v);
mp[v].push_back(u);
}
do {
tmp = res;
for(int i = 1; i <= (n << 1); ++i) {
if(vis[i]) continue;
int pos = -1;
for(int j = 0; j < mp[i].size(); ++j) {
if(vis[mp[i][j]]) continue;
if(pos == -1) pos = j;
else { pos = -1; break; }
}
if(pos != -1) {//配对点唯一
vis[i] = vis[mp[i][pos]] = 1;//将这两个配对
res += 2;
}
}
} while(tmp != res);//没有新的配对了
if(res == (n << 1)) puts("Renko");
else puts("Merry");
}
return 0;
}
D P8347 「Wdoi-6」另一侧的月
我们有一个非常简单的结论, 当出现这种情况时, 显然先手必胜:
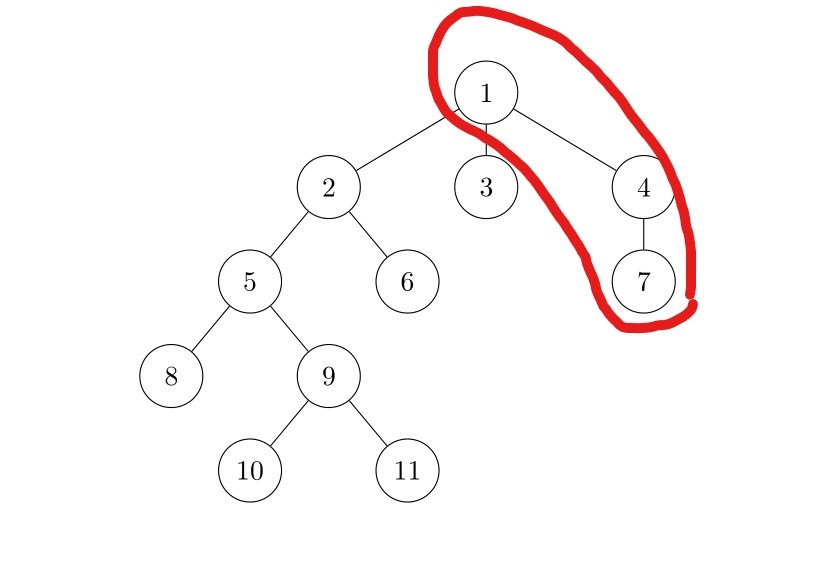
Hifuu 可以取掉 \(1\) , 之后 Luna 怎么取也会剩下一个单独的节点.
我们可以发现 \(4\) 的度数为 \(2\) , \(7\) 的度数为 \(1\) .
于是我们发现 如果一个节点 \(u\) , 和它的儿子 \(v\) 满足 \(in_u = 2, in_v = 1\) 则说明先手必胜.
再考虑扩广: 如果一个节点 \(u\) , 和它的儿子 \(v\) 满足 \(in_u = 2k, in_v = 1\) 则说明先手必胜.
想一下这么一种情况:
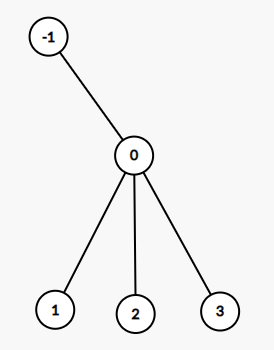
如果 Hifuu 先手取 \(-1\) , 然后指定 \(0\) 这个连通块:
显然任何一个人都不会取掉 \(0\) (这样直接就输掉了), 于是他们只能交替选 \(1\) (Luna) \(2\) (Hifuu), Luna 最后只有 \(0, 3\) 可选, 但她无论选什么都会输, 所以可以简单证明结论正确.
而如果你这么写的话会挂在 subtask 3 , 为什么呢?
我们知道, 在这个子任务中他给定树是完全二叉树, 并且节点数等于 \(2^k - 1\) , 其实就是一个满二叉树最后一层少一个节点, 大概长这样:
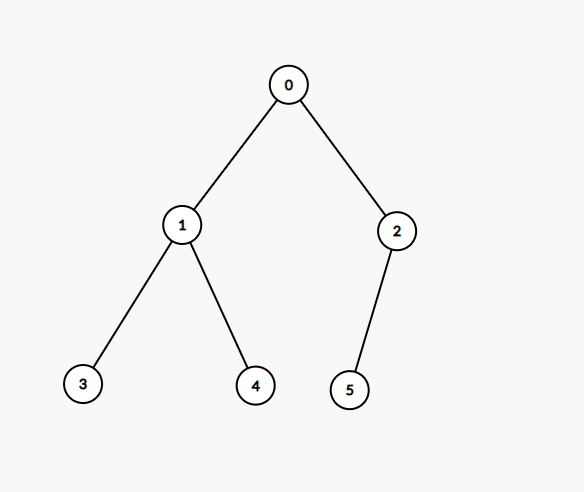
而对于这种情况, 显然选择 \(0\) 这个节点, 再选择 \(2-5\) 这个连通块, 则先手 Hifuu 必胜.
代码的话用 dfs 找 节点 \(u\) , 和它的儿子 \(v\) 满足 \(in_u = 2, in_v = 1\) 即可.
时间复杂度: \(O(n)\)
#include <bits/stdc++.h>
using namespace std;
inline int read() {
int x = 0; char c = getchar(); bool f = 1;
while(c < '0' || c > '9') { if(c == '-') f = 0; c = getchar(); }
while(c >= '0' && c <= '9') { x = x * 10 + c - '0'; c = getchar(); }
return (f ? x : -x);
}
const int N = 1e6 + 10;
int t, n, u, v, in[N];
vector<int> mp[N];
bool res;
inline void dfs(int u, int fa) {
for(auto v : mp[u]) {
if(v == fa) continue;
if(!(mp[u].size() & 1) && mp[v].size() == 1) res = 1;
dfs(v, u);
}
}
int main() {
t = read();
while(t--) {
n = read(); res = 0;
for(int i = 1; i <= n; ++i) { in[i] = 0; mp[i].clear(); }
for(int i = 1; i < n; ++i) {
u = read(); v = read();
mp[u].push_back(v);
mp[v].push_back(u);
}
dfs(1, 0);
if(res || !((n + 1) & n)) puts("Hifuu");//或者满二叉树在最后一层少一个节点也是先手胜
else puts("Luna");
end: ;
}
return 0;
}
E P8348 「Wdoi-6」未知之花魅知之旅
这应该是一道结论题, 可惜我不会, 本来能拿 30 pts 的, 晚了 2s 交题. /ll
30 pts 爆搜卡常代码:
时间复杂度: \(O(3^n)\)
#include <bits/stdc++.h>
using namespace std;
inline int read() {
int x = 0; char c = getchar(); bool f = 1;
while(c < '0' || c > '9') { if(c == '-') f = 0; c = getchar(); }
while(c >= '0' && c <= '9') { x = x * 10 + c - '0'; c = getchar(); }
return (f ? x : -x);
}
int t, a1, a2, x, y, k, l1, l2;
bool res, vis[1500][1500];
int main() {
t = read();
while(t--) {
a1 = read(); a2 = read(); x = read(); y = read(); k = read();
memset(vis, 0, sizeof(vis));
res = 0;
queue<pair<int, int>> q;
if(a1 >= k && a2 >= k) q.push({a1, a2});
while(q.size()) {
l1 = q.front().first; l2 = q.front().second; q.pop();
if(l1 >= 994 || l2 >= 994) continue;
vis[l1][l2] = 1;
if(l1 == x && l2 == y) { res = 1; break; }
if(l1 + l2 >= k && !vis[l2][l1 + l2]) { q.push({l2, l1 + l2}); }
if(l1 - l2 >= k && !vis[l2][l1 - l2]) { q.push({l2, l1 - l2}); }
if(l2 - l1 >= k && !vis[l2][l2 - l1]) { q.push({l2, l2 - l1}); }
}
if(res) puts("yes");
else puts("no");
}
return 0;
}


