树的直径 (树形dp)

定义

树的直径: 树中最长的简单路径.

状态

由于本片讲述的是树形dp方法, 故需要设计状态.
我们令dp[u][0]表示以 \(u\) 为根的子树中最长的简单路径的长度, dp[u][0] 以 \(u\) 为根的子树中次长的简单路径的长度.
那么, 最终答案 \(length = \mathop{max(dp[u][0] + dp[u][1])}\limits_{1 \leq u \leq n}\)

转移

考虑如下情况:

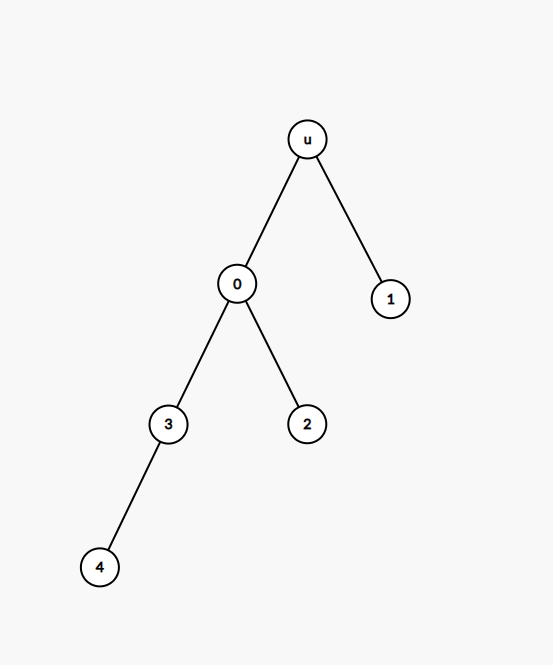
显然,
\(dp[0][0] = length(0 \to 3 \to 4)= 3\)
\(dp[0][1] = length(0 \to 2) = 2\)

思考: 如何从节点 \(0\) 去, 更新节点 \(u\)?
由于 \(0\) 是 \(u\) 的子节点, 将 \(u\) 加入到 \(0\) 中最长路径中 (路径变为u->0->3->4, 长度为 \(4\)), 易得
\(dp[u][0] = \mathop{max(dp[u][0], dp[v][0] + 1)}\limits_{v \ is\ u's\ son}\)

那么 \(dp[u][1]\)呢?
首先明确一点: \(dp[u][0]\) 和 \(dp[u][1]\) 不能同时由一个点更新, 什么意思呢?如下图, 蓝色为最长路径, 红色为次长路径.

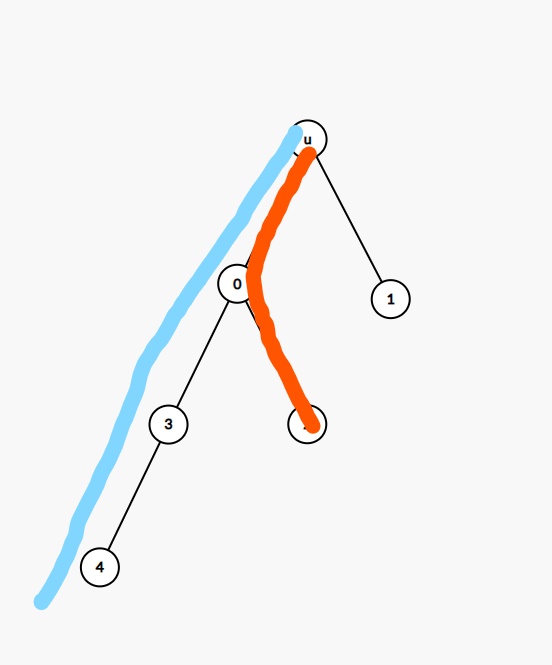
可以发现, 如果由同一点更新, 那么那个重复的点会被 重复经过 ,即 不再是简单路径 .
同样易得: \(dp[u][1] = \mathop{max(dp[u][1], dp[v][0] + 1)}\limits_{v \ is\ u's\ son\ \&\ u\ not\ updated}\)

代码

明确了思路, 代码就很好写了.
核心代码:

inline void dfs(int u, int fa) {//当前的节点点, 当前节点的祖先
    for(int i = head[u]; ~i; i = e[i].nxt) {//链式前向星
        int v = e[i].to;
        if(v == fa) continue;//防止向上走, 这是个常用的小技巧, 不需要记录vis数组
        dfs(v, u);//后序遍历

        if(dp[u][0] < dp[v][0] + 1) { dp[u][1] = dp[u][0]; dp[u][0] = dp[v][0] + 1; }//dp[u][1]得到了除了v以外的最大值 + 1
        else if(dp[u][1] < dp[v][0] + 1) dp[u][1] = dp[v][0] + 1;//确保dp[u][0]没有被更新
        res = max(res, dp[u][0] + dp[u][1]);//更新答案
    }
}