倒谱Cepstrum本质的理解
1.理解:
信号叠加时,不是都是线性关系(时域相互+ 频率相加);有的时候是两种信号成分相乘得到的,(时域卷积,频域相乘):比如很多齿轮啮合时振动信号调制现象,电机的轴向与径向的振动耦合时采集到的振动,声带的冲击(源信号)通过口腔(可以看成滤波器或者系统)发出的声音等等。
通过倒谱可以解析
步骤
1. sigData = x* y卷积 :sigData是采集到的时域信号,x,y是我们想要分离的信号成分。
2. FFT(sigData) = FFT(X) FFT(Y) 频域相乘
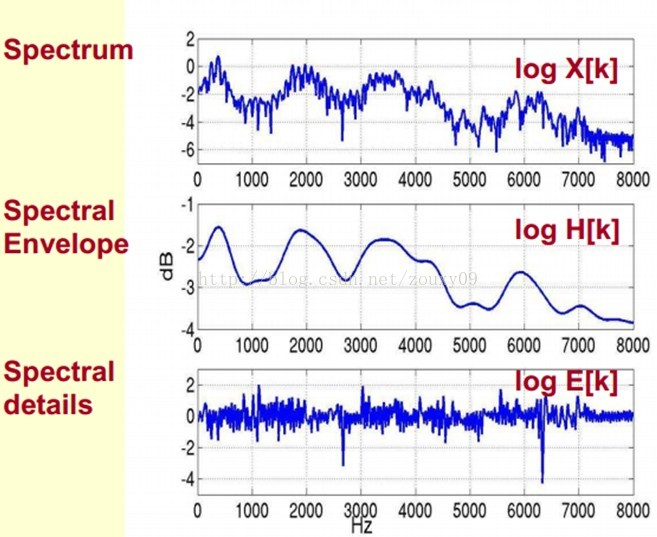
3. log (FFT(sigData)) = log(FFT(X)) + log(FFT(Y) 本质上是将信号同态化,通过 log的性质 把 乘关系的信号 变成 加的关系。比如下图中第一幅图。这时,信号中的频率是第二幅图与第三幅图的线性叠加。下一步我们通过再进行一次FFT(ifft其实本质就是FFT),得到低频部分与高频部分
(图来源见水印)
4. ifft (log (FFT(sigData)) ) 相当于 将第3步骤中得到的频率曲线,当成一个初始信号,再进行一次FFT变换,把这个频率曲线中的高频波动(上面第[3]个子图)和低频趋势(或者叫频率包络)(上面第[2]个子图)分离,以频率的形式解析出来。
IFFT 本质还是FFT,应为FFT与iFFT的结果 , 互为共轭,相差N倍
2.应用:
1. 语音信号中 获取声音信道的方法,MFCC,Mel 频率倒谱系数, 不过里面用的是 DCT, 离散余弦变换(类似FFT)。
2. 变速箱存在故障或振动较大时,采集到的是很多个齿轮与齿轮啮合、存在调制的信号,通过倒谱可以再混杂的信号中找出相关信号频率,进一步找出导致振动大的相关齿轮。
附:
关于 FFT 与 i-FFT的 Matlab 计算结果


