bzoj3684 大朋友的多叉树

Description

我们的大朋友很喜欢计算机科学，而且尤其喜欢多叉树。对于一棵带有正整数点权的有根多叉树，如果它满足这样的性质，我们的大朋友就会将其称作神犇的：点权为1的结点是叶子结点；对于任一点权大于1的结点u，u的孩子数目deg[u]属于集合D，且u的点权等于这些孩子结点的点权之和。
给出一个整数s，你能求出根节点权值为s的神犇多叉树的个数吗？请参照样例以更好的理解什么样的两棵多叉树会被视为不同的。
我们只需要知道答案关于950009857（453*2^21+1，一个质数）取模后的值。

 

Input

第一行有2个整数s,m。
第二行有m个互异的整数，d[1],d[2],…,d[m]，为集合D中的元素。

 

Output

输出一行仅一个整数，表示答案模950009857的值。

 

Sample Input

4 2
2 3

Sample Output

10

HINT

数据规模：

1<=m<s<=10^5, 2<=d[i]<=s，有3组小数据和3组大数据。

 

 

 

 

获得新知识:拉格朗日反演

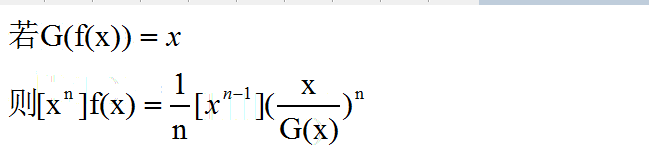
不知道怎么证

结论还是比较好记的

获得新模板:fft的基本操作

//%std
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<algorithm>
#include<cmath>
#include<vector>
#include<queue>
#include<stack>
#include<set>
#include<map>
using namespace std;
#define lovelive long long
#define lc son[x][0]
#define rc son[x][1]
#define lowbit(x) (x&(-x))
#define pt vc
const lovelive mod=950009857,G=7;
const int N=1e5+100;
void read(lovelive &x)
{
  lovelive p=1;
  x=0;
  char c=getchar();
  while(c<'0'||c>'9')
  {
    if(c=='-')
      p=-1;
    c=getchar();
  }
  while(c>='0'&&c<='9')
  {
      x=x*10+c-48;
      c=getchar();
  }
  x*=p;
}
lovelive A[N<<2],B[N<<2],tmp[N<<2],f[N<<2],g[N<<2];
lovelive pow1(lovelive x,lovelive k)
{
  lovelive r=1;
  if(k<0)
    k+=mod-1;
  while(k)
  {
   if(k&1)
     r*=x;
   x*=x;
   r%=mod;
   x%=mod;
   k>>=1;
  }
  return r;
}
void change(lovelive y[],int len)
{
  for(lovelive i=1,j=len>>1,k;i<len-1;i++)
  {
    if(i<j)
      swap(y[i],y[j]);
    k=len>>1;
    while(j>=k)
    {
      j-=k;
      k>>=1;  
    } 
    if(j<=k)
      j+=k;
  }
}
void fft(lovelive y[],int len,int on)
{
  change(y,len);
  for(int h=2;h<=len;h<<=1)
  {
    lovelive wn=pow1(G,(mod-1)*on/h);
    for(int j=0;j<len;j+=h)
    {
      lovelive w=1;
      for(int i=j;i<j+(h>>1);i++)
      {
        lovelive u=y[i],v=w*y[i+(h>>1)]%mod;
        y[i]=(u+v)%mod;
        y[i+(h>>1)]=(u-v+mod)%mod;
        w=w*wn%mod;
      }
    }
  }
  if(on==-1)
  {
    lovelive inv=pow1(len,-1);
    for(int i=0;i<len;i++)
      y[i]=y[i]*inv%mod;
  }
}
void find_inv(lovelive a[],lovelive b[],int len)
{
  if(len==1)
  {
    b[0]=pow1(a[0],-1);b[1]=0;
    return;
  }
  find_inv(a,b,len>>1);
  for(int i=0;i<len;i++)
    f[i]=a[i];
  memcpy(f,a,sizeof(b[0])*len);
  memset(f+len,0,sizeof(f[0])*len);
  fft(f,len<<1,1);
  fft(b,len<<1,1);
  for(int i=0;i<len<<1;i++)
    f[i]=b[i]*(2+mod-f[i]*b[i]%mod)%mod;
  fft(f,len<<1,-1);
  for(int i=0;i<len;i++)
    b[i]=f[i];
  memset(b+len,0,sizeof(b[0])*len);
  return;
}
lovelive inv[N<<2],jc[N<<2];
void find_ln(lovelive a[],lovelive b[],int len)
{
//  for(int i=0;i<len;i++)
//    g[i]=0;
  find_inv(a,g,len);
  for(lovelive i=0;i<len-1;i++)
    b[i]=a[i+1]*(i+1)%mod;
//  b[len]=0;
  fft(g,len<<1,1);
  fft(b,len<<1,1);
  for(int i=0;i<len<<1;i++)
    b[i]=b[i]*g[i]%mod;
  fft(b,len<<1,-1);
  for(int i=len-1;i;i--)
    b[i]=b[i-1]*(inv[i]*jc[i-1]%mod)%mod;
  b[0]=0;
  memset(b+len,0,sizeof(b[0])*len);
  memset(g,0,sizeof(g[0])*len<<1);
}
void find_exp(lovelive a[],lovelive b[],int len)
{
  if(len==1)
  {
    b[0]=1;b[1]=0;
    return;
  }
  find_exp(a,b,len>>1);
  memset(tmp,0,sizeof(tmp[0])*len<<1);
  find_ln(b,tmp,len);
  for(int i=0;i<len;i++)
    tmp[i]=((i==0)+(mod-tmp[i])+a[i])%mod;
  fft(b,len<<1,1);
  fft(tmp,len<<1,1);
  for(int i=0;i<len<<1;i++)
    b[i]=b[i]*tmp[i]%mod; 
  fft(b,len<<1,-1);
  for(int i=0;i<len;i++)
    b[i+len]=0;
  return;
}
void prepare(int len)
{
  jc[0]=inv[0]=1;
  for(lovelive i=1;i<=len;i++)
    jc[i]=jc[i-1]*i%mod;
  inv[len]=pow1(jc[len],-1);
  for(lovelive i=len-1;i>=0;i--)
    inv[i]=inv[i+1]*(i+1)%mod;
}
lovelive C[N<<2];
void find_kth(lovelive a[],lovelive b[],lovelive k,int len)
{
  find_ln(a,C,len);
  for(int i=0;i<len;i++)
    C[i]=C[i]*k%mod;
  find_exp(C,b,len);
}
int main()
{
  lovelive n,s,x,len=1;
  read(s);read(n);
  for(int i=1;i<=n;i++)
  {
    read(x);
    A[x-1]=mod-1;
  }
  A[0]++;
  while(len<=s)
    len<<=1;
  prepare(len);
  find_inv(A,B,len);
  memset(A,0,sizeof(A));
  find_kth(B,A,s,len);
  cout<<A[s-1]*pow1(s,-1)%mod<<"\n";
//  read(n);
//  for(int i=0;i<=n;i++)
//    read(A[i]);
//  while(len<=n)
//    len<<=1;
//  prepare(len);
//  find_exp(A,B,len);
//  for(int i=0;i<=n;i++)
//    printf("%lld ",B[i]);
  return 0;
}
/*
3 2
2 3

4 3
2 3 4

100000 4
2 3 4 5
*/