9月22模拟赛
A. 【雅礼2019.10.25 pm T1】极好的问题
题目
描述
\(Yazid\) 有一个序列 \(A_i(1≤i≤n)\) 和一个质数 \(P\)。
对于一个三元组 \((x,y,z)\),如果满足 \(x≤y≤z\)、\(x×y×z\) \(mod\) \(P=1\),
且存在三个互不相同的下标 \(i,j,k\) 使得 \(A_i=x,A_j=y,A_k=z\) 那么我们就说这个三元组是极好的。
现在,请你求出本质不同的极好的三元组的数目。两个三元组 \((x1,y1,z1),(x2,y2,z2)\) 被认为是本质不同的,当且仅当 \(x1≠x2\) 或 \(y1≠y2\) 或 \(z1≠z2\) 。
如果你能自如地运用你学习的算法解决这个极好的问题,那么你就会获得“Wow”的赞美,这将是你独享的时刻。
输入格式
第一行 \(2\) 个用空格隔开的整数 \(n,P\)。
第二行 \(n\) 个用空格隔开的整数 \(A_1,...,A_n\)。
输出格式
输出一行一个整数,表示极好的三元组的数目。
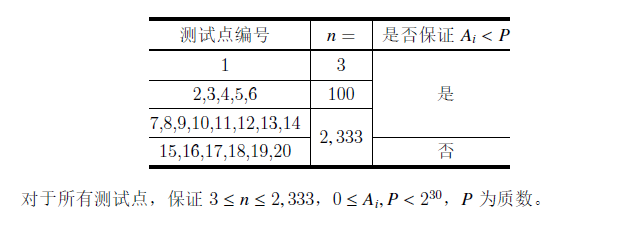
思路
首先根据题目要求,对给出的 \(A\) 序列进行去重计数操作。并算出每种数的乘法逆元。
\(\mathfrak{talk\; is\; easy\; show\; me\; the\; code}\)
inline void pre(){
sort(a+1,a+1+n);b[1]=a[1];cnt=1;s[1]=1;
for(int i=2;i<=n;i++){
if(a[i]!=a[i-1]) b[++cnt]=a[i],s[cnt]=1;
else s[cnt]++;
}
for(int i=1;i<=cnt;i++) inv[i]=qpow(b[i],P-2);
}
极好的三元组有以下三种情况:
-
\(a\times a\times a\)
-
\(a\times a\times b\)
-
\(a\times b\times c\)
对于第一种情况,可以统计每个出现次数大于等于 \(3\) 的数的三次方 (在 \(mod\) \(P\) 意义下) 是否等于 \(1\) 。
对于第二种情况,统计每个出现次数大于等于 \(2\) 的数的二次方乘去重序列中的其它数 (在 \(mod\) \(P\) 意义下) 是否等于 \(1\)
\(\mathfrak{talk\; is\; easy\; show\; me\; the\; code}\)
for(int i=1;i<=cnt;i++){
if(s[i]>=3)
if(b[i]*b[i]%P*b[i]%P==1) ans++;
if(s[i]>=2)
for(int j=1;j<=cnt;j++){
if(j==i) continue;
if(b[i]*b[i]%P*b[j]%P==1)ans++;
}
}
对于第三种情况,预处理出所有两个不同的数的乘积,并在预处理中特判 \(a\times b=a'\) 或 \(a\times b=b'\) 的情况。因为此时等价于情况二,不特判会导致重复计算。
\(\mathfrak{talk\; is\; easy\; show\; me\; the\; code}\)
for(int i=1;i<=cnt;i++)
for(int j=i+1;j<=cnt;j++) {
cj[++tot]=b[i]*b[j]%P;
if(cj[tot]==inv[i]) q++;
if(cj[tot]==inv[j]) q++;
}
sort(cj+1,cj+1+tot);
接下来利用upper_bound 和 lower_bound 作差得出每个数的乘法逆元在这些乘积中出现的次数。这些次数之和会反复出现三次如:
所以最后需要除 \(3\) 。
最后的最后:记得开\(long\) \(long\) ,记得随时 mod P
code
完整代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=6e6+105;
int a[N],b[N],s[N],P,inv[N],n,cnt,cj[N],ans,tot;
inline int qpow(int a,int b){
int res=1;
while(b){
if(b&1)res=res*a%P;
a=a*a%P;b>>=1;
}
return res%P;
}
inline void pre(){
sort(a+1,a+1+n);b[1]=a[1];cnt=1;s[1]=1;
for(int i=2;i<=n;i++){
if(a[i]!=a[i-1]) b[++cnt]=a[i],s[cnt]=1;
else s[cnt]++;
}
for(int i=1;i<=cnt;i++) inv[i]=qpow(b[i],P-2);
}
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*f;
}
inline int count(int k){
int x=upper_bound(cj+1,cj+1+tot,k)-cj;
int y=lower_bound(cj+1,cj+1+tot,k)-cj;
return x-y;
}
signed main(){
n=read();P=read();
for(int i=1;i<=n;i++) a[i]=read();
pre();
for(int i=1;i<=cnt;i++){
if(s[i]>=3)
if(b[i]*b[i]%P*b[i]%P==1) ans++;
if(s[i]>=2)
for(int j=1;j<=cnt;j++){
if(j==i) continue;
if(b[i]*b[i]%P*b[j]%P==1)ans++;
}
}
int q=0;
for(int i=1;i<=cnt;i++)
for(int j=i+1;j<=cnt;j++) {
cj[++tot]=b[i]*b[j]%P;
if(cj[tot]==inv[i]) q++;
if(cj[tot]==inv[j]) q++;
}
sort(cj+1,cj+1+tot);int res=0;
for(int i=1;i<=cnt;i++) res+=count(inv[i]);
res-=q;
printf("%d",res/3+ans);
return 0;
}
D. 【长郡-NOIP2017模拟Day2-T2】座位安排
题目
描述
费了一番口舌,\(wfj_2048\) 终于成功的说服了 \(n∗m\) 个朋友来陪自己看电影。为了这次声势浩大的行动, \(wfi_2048\) 包下了一座有 \(n∗m\) 个座位的电影院。(\(wfj_2048\) 坐哪?我也不知道。。。。。。)
电影院前门的坐标为 \((0,0)\) ,后门的坐标为 \((0,m+1)\) 。有 \(k\) 个朋友站在前门外,剩下的 \(n∗m−k\) 个站在后门外。
但是,问题来了:每个朋友都有一个不一定相同的忍耐值 \(s\),若从她到达的门到座位的曼哈顿距离超过 \(s\) ,她会感到不爽并离开,可 \(wfi2048\) 不想错过任何一个朋友。于是,他想让你告诉他:是否存在一种方案,使得所有的朋友都能安排到合适的座位,且没有朋友会离开?
输入格式
第一行为 \(n\) 和 \(m\) ,意义如描述之所示
第二行一个整数 \(k\) ,接着 \(k\) 个整数描述前门外的 \(k\) 个朋友的 \(s\) 值
第三行一个整数 \(n∗m−k\) 个数描述后门外的朋友的 \(s\) 值
输出格式
若存在合法的座位安排方案则输出YES,否则输出NO
思路
凭运气做法:
#include<bits/stdc++.h>
using namespace std;
int myrand() {
std::mt19937 rng;
rng.seed(std::random_device()());
std::uniform_int_distribution<std::mt19937::result_type> dist2(1,10);
return dist2(rng);
}
int main(){
cout<<(myrand()<=6?"YES":"NO");
}
证据:
卡评测机,像这样:
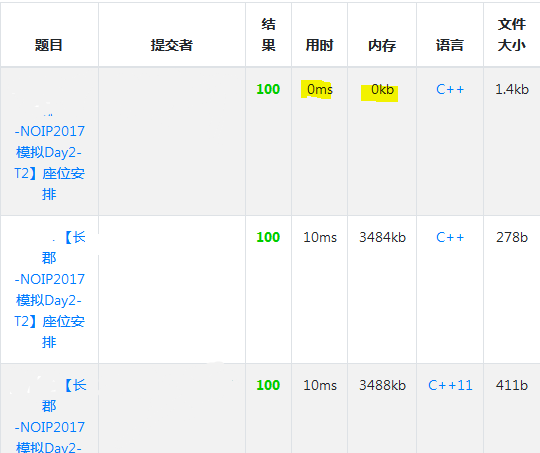
和std的数据结构法不同,其实只需要一个很基础的贪心即可解决问题。
考虑一个事情:忍耐值越小越容易找不到座位。所以我们首先给忍耐值小的人安排座位。而且让他们尽量坐得远
对于从前入口和后入口进入的人,他们呈这样分布:
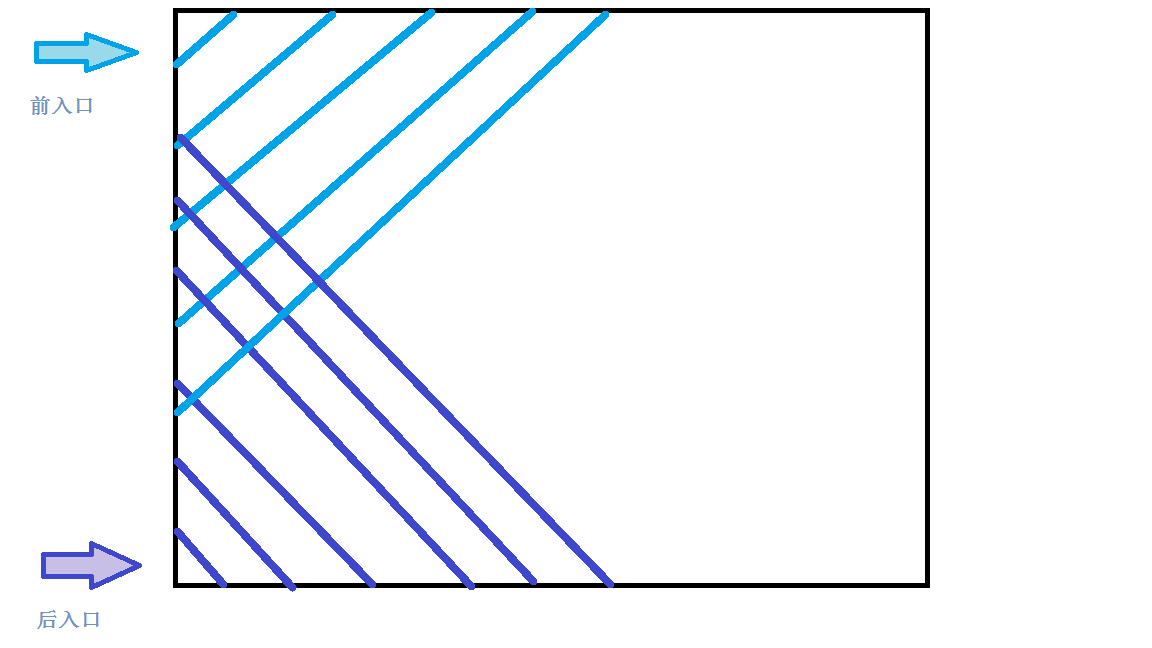
所以为了给后入口腾地方,前入口进的人的座位的列数应该尽量大。同理,后入口也是。
不同于std,这里将所有人的忍耐度都按从小到大排序,并记录一个\(qh\) 表示是从前进还是从后进。
用数组 \(vs[N][2]\) 来记录某一忍耐值的斜线是否坐满。
如 \(vs[3][1]=1\) 表示:从前入口进,\((2,1),(1,2)\) 都已经坐满。
最后,记得处理初始数据。
因为题目保证: \(n*m≤100000\) , 但是没有保证忍耐值 \(s\) 的大小。
所以:
int x=read();if(x>n+m) x=n+m;
不这么做会 \(RE\) 。
有关其他玄学优化
由于按照 \(s\) 排序后,越往后出现 NO 答案的可能性就越小,所有就有类似于模拟退火的这类优化:
\(\mathfrak{talk\; is\; easy\; show\; me\; the\; code}\)
while(t>1e-12 && i<=sum){
flag=1;
check(p[i].s,p[i].qh);
if(flag==1){printf("NO");return 0;}
i++;t*=d;
}
printf("YES");
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e7+105;
bool mp[6105][6105];
int n,m,k1,k2,cnt;//qm[N],hm[N];
struct qwq{
bool qh;//qh->0,q;qh->1,h
int s;
}p[N];
bool cmp(qwq a,qwq b){return a.s<b.s;}
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*f;
}
bool vs[N][2],flag;
inline void check(int s,int kind){
if(kind==0){
for(int i=s;i>=2;i--){
if(vs[i][0]==1) continue;
for(int j=min(i-1,m);j>=1;j--)
if(mp[i-j][j]==0)
{flag=0;mp[i-j][j]=1;break;}
if(flag==1) vs[i][0]=1;
else if(flag==0) return ;
}
}
else{
for(int i=s;i>=2;i--){
if(vs[i][1]==1) continue;
for(int j=min(i-1,m);j>=1;j--)
if(mp[m-(i-j)+1][j]==0)
{flag=0;mp[m-(i-j)+1][j]=1;break;}
if(flag==1) vs[i][1]=1;
else if(flag==0) return ;
}
}
}
int main(){
n=read();m=read();k1=read();
int sum=n*m;
for(int i=1;i<=k1;i++){
int x=read();if(x>n+m) x=n+m;
p[++cnt].s=x;
p[cnt].qh=0;
}
k2=read();
for(int i=1;i<=k2;i++){
int x=read();if(x>n+m) x=n+m;
p[++cnt].s=x;
p[cnt].qh=1;
}
sort(p+1,p+1+sum,cmp);
int i=1;
while(i<=sum){
flag=1;
check(p[i].s,p[i].qh);
if(flag==1){printf("NO");return 0;}
i++;if(i>sum) break;
}
printf("YES");
return 0;
}
E. 【雅礼2019.11.03pm-T3】红心大战
题目
描述
Resee在欢乐地和朋友们打红心大战,想请你帮她统计一下分数~
具体地游戏规则如下:
共有 \(4\) 个玩家,\(52\) 种牌
牌有"2,3,4,5,6,7,8,9,10,J,Q,K,A"自小到大种点数; 黑桃( \(S\) ), 红桃( \(H\) ), 梅花( \(C\) ), 方块( \(D\) )
一张牌由一种花色和一种点数组成
在每一回合中,每个玩家各出一张牌,点数最大的牌中最先出牌的人为该轮的赢家,四张牌被置入赢家的弃牌堆中。所有回合结束后,对于每个玩家弃牌堆中的牌独立进行结算,分两个步骤:
第一步,玩家拿出所有种类红桃牌各一张和一张黑桃 \(Q\),丢弃它们并且给其他玩家各加 \(26\) 分,重复以上过程直到不能作出这个操作
第二步,一张一张丢弃剩下所有的牌,如果这张牌是红桃则给自己加 \(1\) 分,如果是黑桃 \(Q\) 则给自己加 \(13\) 分,其他牌分数不变
输入格式
第一行一个整数 \(n\) 表示回合数
接下来四行四个字符串,依次表示四个人的名字
接下来 \(4∗n\) 行表示出的牌,三个字符串依次表示出牌的人,牌的花色,牌的点数
输出格式
四行按照输入顺序依次输出四个人的得分
思路
小模拟题,根据题意写代码。
坑点:
-
注意
10的读入 -
注意测试点中有
红桃1这张不存在的牌。 -
注意减掉一套红桃牌的同时记得减掉一张黑桃 \(Q\)
code
#include<bits/stdc++.h>
using namespace std;
int n,j;
struct wanjia{
string name;
int qp[5][21],fen;
}p[5];
struct zhuopai{int cnt,mx,belong;}zp;
struct pai{int num,hua;}zpai[11];
inline void pre(){
zp.mx=-1;zp.cnt=0;zp.belong=-1;j=0;
memset(zpai,0,sizeof(zpai));
}
inline int ZH(char c){
if(c=='S') return 1;
else if(c=='H') return 2;
else if(c=='C') return 3;
else if(c=='D') return 4;
}
inline int ZN(char c,char c2){
int x=0;
if(c=='1' && c2=='0') x=10;
else if(isdigit(c)) x=c-'0';
else{
if(c=='J') x=11;
else if(c=='Q') x=12;
else if(c=='K') x=13;
else if(c=='A') x=14;
}
return x;
}
inline void chupai(int k){
char Hua,Num[2];int zh,zn;char c2;
cin>>Hua;cin>>Num;
zh=ZH(Hua);zn=ZN(Num[0],Num[1]);
if(zp.mx==-1) {zp.mx=zn,zp.belong=k;}
else if(zn>zp.mx){zp.mx=zn;zp.belong=k;}
zpai[++zp.cnt].num=zn;zpai[zp.cnt].hua=zh;
}
inline void mljs(int k){
for(int i=1;i<=zp.cnt;i++)
p[k].qp[zpai[i].hua][zpai[i].num]++;
}
inline void zjs(int k){
bool flag=1;
while(1){
for(int i=2;i<=14;i++)
if(p[k].qp[2][i]<=0){flag=0;break;}
if(p[k].qp[1][12]<=0) flag=0;
if(flag==0) break;
else{
for(int i=2;i<=14;i++)p[k].qp[2][i]--;
p[k].qp[1][12]--;
for(int i=1;i<=4;i++)if(i!=k) p[i].fen+=26;
}
}
for(int i=2;i<=14;i++)
if(p[k].qp[2][i]!=0)
p[k].fen+=p[k].qp[2][i],p[k].qp[2][i]=0;
if(p[k].qp[1][12]!=0)
p[k].fen+=p[k].qp[1][12]*13,p[k].qp[1][12]=0;
}
int main(){
cin>>n;
for(int i=1;i<=4;i++) cin>>p[i].name;
while(n--){
pre();
for(int i=1;i<=4;i++){
string s;cin>>s;
for(j=1;j<=4;j++) if(p[j].name==s) break;
chupai(j);
}
mljs(zp.belong);
}
for(int i=1;i<=4;i++) zjs(i);
for(int i=1;i<=4;i++) printf("%d\n",p[i].fen);
return 0;
}

 乘法逆元,分块+树链剖分,小模拟,贪心,基于贪心的dp
乘法逆元,分块+树链剖分,小模拟,贪心,基于贪心的dp

 浙公网安备 33010602011771号
浙公网安备 33010602011771号