9月13日模拟赛
A. [2019.10长郡集训day12]古代龙人的谜题
题目
描述
\(Mark Douglas\) 是一名调查员。他接受了「调查古代龙人」的任务。经过千辛万苦,\(Mark\) 终于找到了一位古代龙人。\(Mark\)找到他时,他正在摆弄一些秘药, 其中一些药丸由于是从很久以前流传下来的,发出了独特的光泽。古代龙人告诉了\(Mark\) 一些他想知道的事情,看了看手中的秘药,决定考一考这位来访者。
古代龙人手中共有 \(n\) 粒秘药,我们可以用 \(1\) 表示「古老的秘药」,其余的用 \(0\) 表示。他将它们排成一列。古代龙人认为平衡是美的,于是他问 \(Mark\) 能选出 多少个「平衡的区间」。「平衡的区间」是指首先选出一个区间 \([L, R]\) ,在它内部 选出一个中间点 \(mid\) ,满足 \(L<mid<R\) ,\(mid\) 是「古老的秘药」,且区间 \([L, mid]\) 和 \([mid, R]\) 中「古老的秘药」个数相等。
输入格式
第一行为一个正整数 \(idx\) 表示该测试点所属的子任务编号,子任务的详细信 息请见「数据范围」。样例的子任务编号为 \(0\)。
第二行为一个正整数 \(n\)。
第三行为一个长度为 \(n\) 的字符串,仅包含 \(0\) 和 \(1\)。
思路
把这个 \(01\) 序列称为序列 \(a\) 。那么可以观察到,答案的贡献来源于两个部分:
-
对于合法区间 \([a_i,a_j]\) , \(a_i,a_j\) 为 \(1\) 。称其为基本的区间。
-
由基本区间向外扩展得到的区间。
-
由一堆 \(0\) 包围的 \(1\)
三种情况如图:
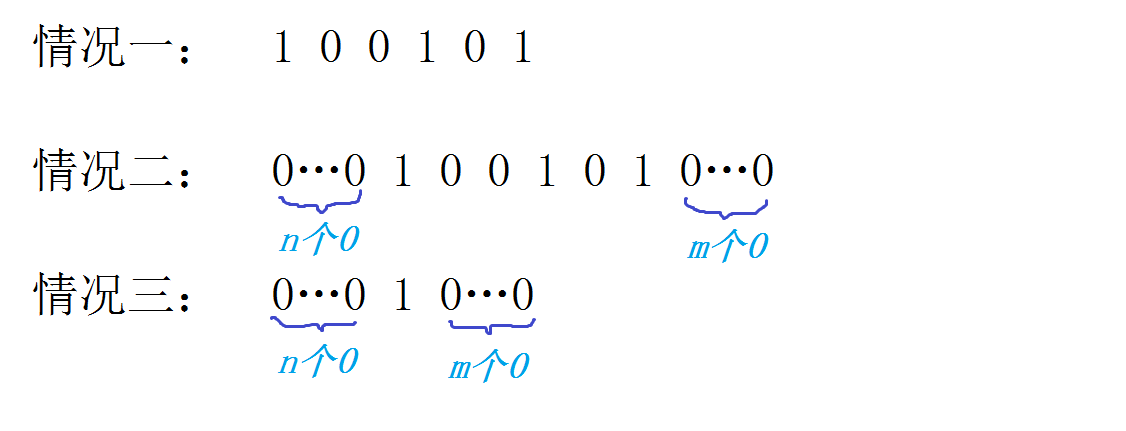
对于以上三种情况,处理出每个 \(1\) 到前一个 \(1\) 中间有多少个 \(0\) (记做 \(L\)) ,再处理出每个 \(1\) 到后一个 \(1\) 中间有多少个 \(0\) (记做 \(R\)),就可以解决 情况三 。在解决 情况一 的基础上就可以解决 情况二 。
根据乘法原理(\(n,m\)的意义如图):
情况三的贡献为: \(n\times m\)
情况二的贡献为:\((n+1)\times (m+1)\)
现在考虑怎么解决情况一,只考虑左右端点皆为 \(1\) 的情况:
假设序列 \(a\) (黑色部分)如下:
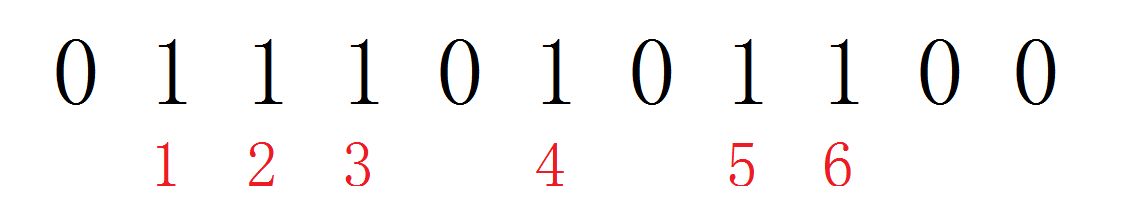
把所有的 \(1\) 按照从左到右的顺序排号,对于 \(a_i\) 称它的序号为 \(k_i\) 。(红色部分)
有一条显而易见的结论是一个合法的区间中,\(1\) 的个数是奇数。
假设有一个合法区间 \([a_i,a_j]\) 那么,\(k_i\) 和 \(k_j\) 的奇偶性是相同的。
对于这一点,预处理出每个 \(a_i=1\) 的 \(R_i\) ,求出两个值:
和
对于序列 \(a\) 中的每个 \(1\) ,尝试计算它作为左端点的贡献(情况一二)
于是有(假设这个数为 \(a_i\),选择的右端点为\(a_j\)):
那么总贡献为:
其中 \(J\) 表示 所有的可以作为右端点的\(a_j\)
再加上情况三的贡献,那么就是:
预处理出 \(R\) ,\(q_0\) , \(q_1\)后,从左到右扫一遍,每次计算前让 \(q_{0/1}-=R_i\) 就可以迅速得出 \(\sum\;(R_J+1)\) ,总复杂度应该是 \(O(n)\) 。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+105;
int opt,n,cnt1,a[N],r[N],q0,q1,ans;
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*f;
}
inline int spread(){
int x=0;char ch=getchar();
while(!isdigit(ch)){ch=getchar();}
if(isdigit(ch))x=ch-'0';
return x;
}
signed main(){
opt=read();
if(opt>=0){
n=read();
for(int i=1;i<=n;i++)a[i]=spread(),cnt1+=a[i];
int k=cnt1;
for(int i=n,j=0;i>=1;i--){j++;if(a[i]==1){r[k--]=j;j=0;}}
for(int i=1;i<=cnt1;i++){if(i%2==0) q0+=r[i];else q1+=r[i];}
k=1;
for(int i=1,j=0;i<=n;i++){
j++;
if(a[i]==1)
if(k%2==0)
{ans+=(j-1)*(r[k]-1)+j*(q0-r[k]);q0-=r[k];k++;j=0;}
else
{ans+=(j-1)*(r[k]-1)+j*(q1-r[k]);q1-=r[k];k++;j=0;}
}
printf("%lld",ans);
}
return 0;
}
B. [2019.10长郡集训day17]石头剪刀布
题目
描述
\(wzms\) 今年举办了一场剪刀石头布大赛, \(bleaves\) 被选为负责人。
比赛共有\(2^n\)个人参加, 分为 \(n\) 轮,
在每轮中,第 \(1\) 位选手和第 \(2\) 位选手对战,胜者作为新的第 \(1\) 位选手,
第 \(3\) 位和第 \(4\) 位对战,胜者作为新的第 \(2\) 位选手,以此类推。
\(bleaves\) 调查得知,每个人都有其偏爱决策,每个人在每一次对战中都会使用他的偏爱决策。
如果一次对战的双方的偏爱决策相同,那么这次对战就永远不会结束,所以 \(bleaves\) 不希望这种情况发生。
现在 \(bleaves\) 知道了每个人的偏爱决策,但她不知道如何安排初始的次序,使得上面的情况不会发生,你能帮帮她吗?
输入格式
一行三个整数 \(R,P,S\) ,表示偏爱石头,布,剪刀的人数分别为 \(R,P,S\) 。
输出格式
如果无解,输出 \(IMPOSSIBLE\) ;
否则输出一个长度为 \(R+P+S\) 的字符串,第 \(i\) 个字符表示初始时第 \(i\) 位选手的偏爱决策,
如果有多种方案,输出字典序最小的
思路
首先,假设最后胜出的是偏爱 石头/剪刀/布 的人,实际上答案是固定的。
先预处理出字典序最小的固定答案,再判断是否可行,如果可行,直接输出预处理出的答案。
这里有一个小换元。假设第 \(i\) 层的个数分别为 \(R_i,P_i,S_i\)。按照合法的规定向上推上一层的 \(R_{i-1},P_{i-1},S_{i-1}\) 那么有:
最终得到结果:
如果 \(R_{i-1},P_{i-1},S_{i-1}\) 中的任意一个值小于 \(0\) ,那么此时无解。
此外,等于 \(0\) 是可能有解的
code
#include<bits/stdc++.h>
const int N=35;
using namespace std;
int p,r,s;
string xp[N],xr[N],xs[N];
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*f;
}
inline void pre(){
xp[0]="P",xr[0]="R",xs[0]="S";
for(int i=1;i<=20;i++){
xp[i]=min(xp[i-1]+xr[i-1],xr[i-1]+xp[i-1]);
xr[i]=min(xr[i-1]+xs[i-1],xs[i-1]+xr[i-1]);
xs[i]=min(xs[i-1]+xp[i-1],xp[i-1]+xs[i-1]);
}
}
inline void work(){
int n=0;r=read();p=read();s=read();
while((1<<n)!=(r+p+s))n++;
int nn=n;
while(n){
int x=(r+p-s)/2;
int pr=x,ps=p-pr,rs=r-pr;
if(pr<0 || ps<0 || rs<0) {puts("IMPOSSIBLE");exit(0);}
p=pr,s=ps,r=rs;n--;
}
if(p)cout<<xp[nn];
if(r)cout<<xr[nn];
if(s)cout<<xs[nn];
}
int main(){
pre();work();return 0;
}
C. [2019.10长郡集训day17]投票
题目
描述
老师让 \(bleaves\) 组织一场投票来调查同学们对 \(kcz\) 出题的评价。
投票有两种选择,一种是好,一种是坏。
一共有 \(n\) 个同学, \(bleaves\) 知道第 \(i\) 个同学有 \(p_i\) 的概率投"好"。 \(bleaves\) 觉得 \(kcz\) 出题很 \(nice\) ,但她知道 \(kcz\) 出题很辛苦,所以她希望选出 \(k\) 个同学投票,使得平票的概率最大。
你能帮她求出这个最大值吗?
输入格式
第一行两个正整数 \(n\) , \(k\) 。
接下来一行 \(n\) 个实数,第 \(i\) 个数为 \(p_i\) ,保证小数点后有 \(2\) 位。
输出格式
一行一个实数表示答案,当你的答案与标准答案的绝对误差不超过 \(10^{-6}\) 时即认为正确。
思路
code
#include<bits/stdc++.h>
#define d double
using namespace std;
const int N=2e3+105;
int n,k;
d p[N],ans,pre[N][N],suf[N][N];
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*f;
}
int main(){
n=read();k=read();
for(int i=1;i<=n;i++) scanf("%lf",&p[i]);
sort(p+1,p+1+n);
pre[0][0]=suf[0][0]=1;
for(int i=1;i<=k;i++)for(int j=0;j<=i;j++){
pre[i][j]=pre[i-1][j]*(1-p[i]);
if(j)pre[i][j]+=pre[i-1][j-1]*p[i];
suf[i][j]=suf[i-1][j]*(1-p[n-i+1]);
if(j)suf[i][j]+=suf[i-1][j-1]*p[n-i+1];
}
for(int i=0;i<=k;i++){
double tmp=0;
for(int j=0;j<=k/2;j++) tmp+=pre[i][j]*suf[k-i][k/2-j];
ans=max(ans,tmp);
}
printf("%lf\n",ans);
return 0;
}
D. [2019.10长郡集训day21]小学组
题目

思路
code
#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+9;
const int N=31;
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return x*f;
}
int n,m;
char op;
long long a[N],res[N],X,ans;
void dfs(int pos,long long tot,long long cnt){
if(pos>n){if(res[pos]!=X)return;(ans+=cnt)%=mod;return;}
if(op=='&'&&(res[pos]&X!=X))return ;
if(op=='|'&&(res[pos]&(~X)))return ;
res[pos+1]=res[pos];dfs(pos+1,tot,cnt);
if(op=='&')res[pos+1]=res[pos]&a[pos];
else if(op=='|')res[pos+1]=res[pos]|a[pos];
else res[pos+1]=res[pos]^a[pos];
dfs(pos+1,tot+1,cnt*(tot+1)%mod);
}
int main(){
scanf("%s",&op);scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)for(int j=1,x;j<=m;j++)
{x=read();a[i]=(a[i]<<1)+x;}
for(int i=1,x;i<=m;i++){x=read();X=(X<<1)+x;}
for(int i=1;i<=n;i++){res[i+1]=a[i];dfs(i+1,1,1);}
printf("%lld",ans);
return 0;
}

 考试
考试

