近期模拟赛1
9月4号前言
写挂了+没开long long 造成的40分惨剧( 136->40 )
T1 [FJSC2021D9T1]殖民主义
题目
西班牙与葡萄牙是新航线的开辟者和早期殖民者的代表,当时的殖民主义者有一个基本逻辑:欧洲以外的世界,均为“无主的土地”;非基督教徒,都不是“上帝”的子民,可以彻底地剥夺他们的一切权利。
假设世界上有 \(n\) 个地区,相互之间有 \(n−1\) 航道将其连通,初始时西班牙仅占有地区 \(1\),葡萄牙仅占有地区 \(n\),其他地区均为“无主的土地”。
每次西班牙和葡萄牙会轮流进行活动,他们会从己方以占有的一个地区中派出一支探险队,前往一个与之相邻的“无主的土地”将其占为己有,进行殖民统治。
双方都会尽可能的占领多的殖民地,并且使得对方的殖民地尽可能少。
问如果在西班牙最先派出探险队的情况下,最终哪个国家占领的土地最多。
思路
额,其实这个题很简单。
以 \(1\) 为根。
首先,如果对方的必经路线上有一个点已经被占了,那么对方最多只能占这个点的儿子节点。
所以最优的策略是,两个国家去争夺\(1——n\)这条链上的点。
所以\(dfs\)处理出子树大小和父亲数组。那么葡萄牙能争夺到的点数就是这条链上的二分之一位置的点的\(siz\)
比较\(n-siz[pos]\)和\(siz[pos]\)的大小即可。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+105;
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*f;
}
int t,n,S,P;
int d[N],siz[N],f[N];
bool v[N];
int nex[N],to[N],h[N],cnt;
inline void add(int x,int y){to[++cnt]=y;nex[cnt]=h[x];h[x]=cnt;}
void dfs(int x){
v[x]=1;siz[x]=1;
for(int i=h[x];i;i=nex[i]){
if(v[to[i]])continue;
f[to[i]]=x;
d[to[i]]=d[x]+1;
dfs(to[i]);
siz[x]+=siz[to[i]];
}
}
inline void pre(){
memset(d,0,sizeof(d));d[1]=1;
memset(v,0,sizeof(v));
memset(nex,0,sizeof(nex));memset(to,0,sizeof(to));
memset(h,0,sizeof(h));cnt=0;
memset(f,0,sizeof(f));
S=0,P=0;
}
int jump(int x,int sum){
int j1=x,j2=x;int cnt=0;
while(1){
if(cnt>=(sum/2)) break;
j1=f[j1];
cnt++;
}
//printf("%d",j1);
return j1;
}
int main(){
t=read();
while(t--){
n=read();pre();
for(int i=1,x,y;i<n;i++){
x=read(),y=read();
add(x,y);add(y,x);
}
dfs(1);
int x=d[n]-d[1]-1;
int pos=jump(n,x);
P+=siz[pos];
S=n-P;
//printf("%d %d\n",S,P);
if(S>P)printf("Spain\n");
else printf("Portugal\n");
}
return 0;
}
9月8日前言
我这天的博客本来已经写完一半的……但是我就中途离开一下……
台式机被强制关机,还没来得及保存……然后就什么都不剩下了。于是我得重写。哎……
T1【2018.8雅礼8.12T1】a
题目
描述
给定一个 \(n∗m\) 的 \(01\) 矩阵,求包含 \([l,r]\) 个 \(1\) 的子矩形个数。
输入格式
第一行,两个正整数 \(n,m\)。
接下来 \(n\) 行,每行一个长度为 \(m\) 的 \(01\) 串,表示给定的矩阵。
接下来一行,两个自然数 \(l,r\)。
思路
前缀和加暴力,如图:
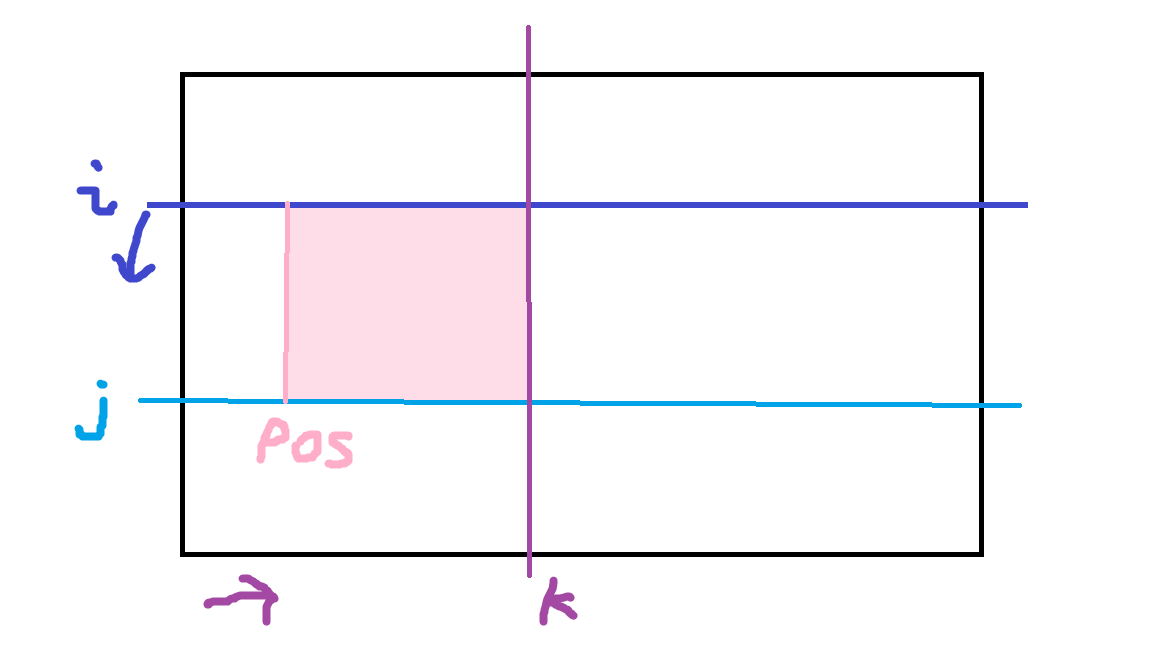
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=35,M=5e4+105;
int n,m,l,r,mp[N][M],q[N][M],s[M],ans;
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*f;
}
inline int spread(){
int x=0;char ch=getchar();
while(!isdigit(ch)){ch=getchar();}
if(isdigit(ch)){x=ch-'0';}
return x;
}
signed main(){
n=read();m=read();
for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)mp[i][j]=spread();
for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)
{q[i][j]=q[i-1][j]+q[i][j-1]-q[i-1][j-1]+mp[i][j];}
l=read();r=read();
for(int i=1;i<=n;i++)for(int j=i;j<=n;j++){
int a=0,b=0;
for(int k=1;k<=m;k++){
s[k]=q[j][k]-q[i-1][k];
while(s[k]-s[a]>=l && a<k) a++;
while(s[k]-s[b]>r && b<k) b++;
ans+=a-b;
}
}
printf("%lld",ans);
return 0;
}
T5 【雅礼2019.10.17amT2】苹果树
题目
描述
小 \(B\) 是一个辛勤的农民,他家里种了一棵很大的苹果树。
这棵苹果树可以看作一张 \(n\) 个点 \(n−1\) 条边的无向连通图,小B觉得这颗苹果树很脆弱,因为只要剪断任意一条边,苹果树就不连通了,于是他给苹果树新加了 \(m\) 条边。
现在这颗苹果树就不像是一棵树了,成了一张 \(n\) 个点 \(n+m−1\) 条边的无向连通图,小 \(Q\) 是小 \(B\) 的好朋友,他觉得这棵树依然很脆弱,他告诉小 \(B\) ,自己只要破坏两条边,一条是原树中的边,一条是小B新加的边,就能使苹果树不连通。
小 \(B\) 觉得小 \(Q\) 说得很不可思议,于是他找来了擅长编程的你,希望你告诉他,按照小 \(B\) 的破坏规则,有多少种不同的方案使得苹果树不连通。
注意:两种方案不同当且仅当一条边在第一种方案中被删除了但在第二种方案中没有被删除。
输入格式
第一行两个正整数 \(n,m\),表示苹果树的点数和后面新加的边的个数。
接下来 \(n−1\) 行,每行两个正整数 \(u,v\) ,表示 \((u,v)\) 之间有一条树边。
接下来 \(m\) 行,每行两个正整数 \(u,v\),表示包 \((u,v)\) 之间有一条小 \(B\) 新加的边。
输出格式
输出一行一个整数,表示有多少种不同的方案。
思路
树上差分。(再见了树链剖分)
把初始的,还没有加边的图上的边称为树边,将后添加的边称为非树边。
假设初始图是这样的:
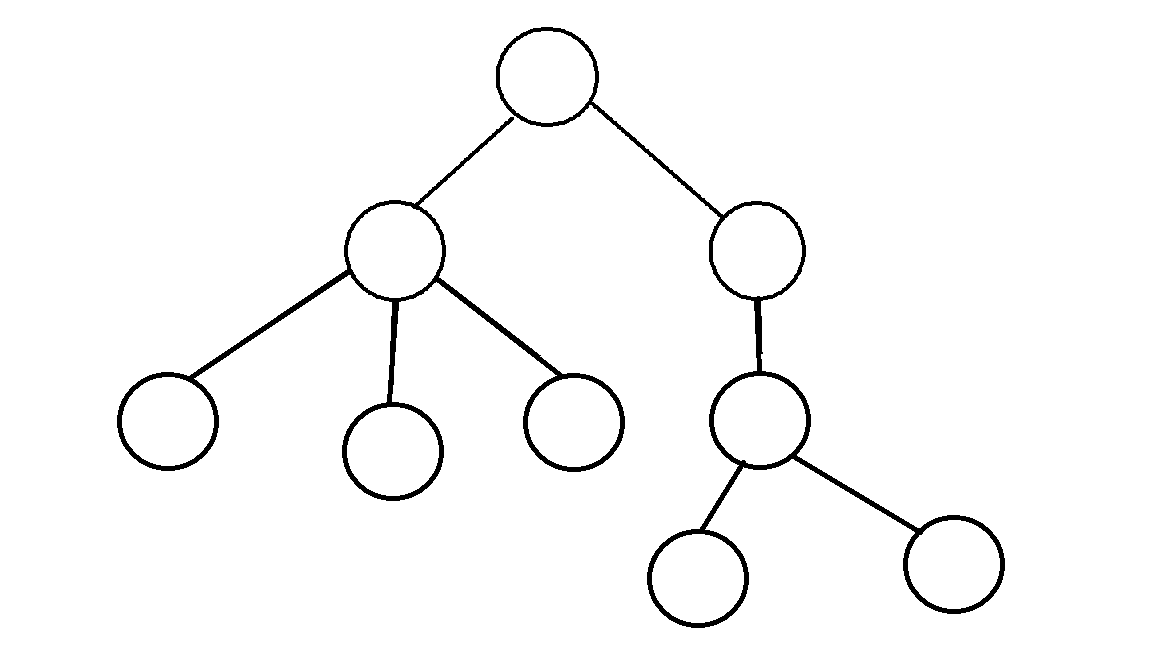
此时,图是一棵树。任意在树上添加一条非树边(橙色):
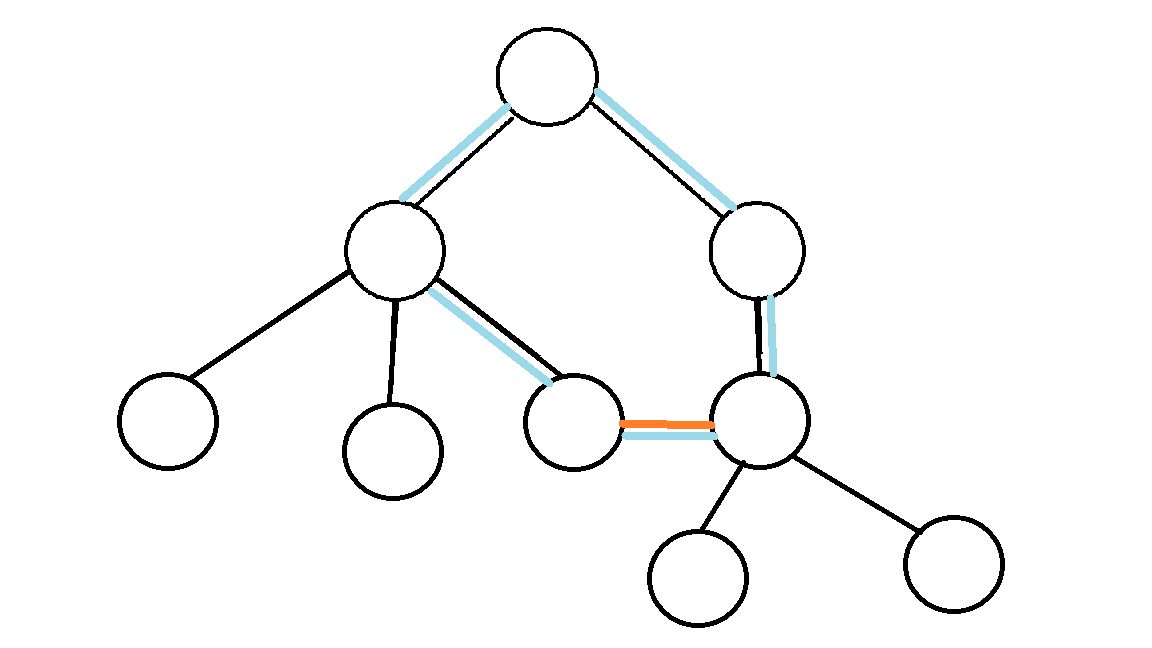
图上会出现一个环。(图中蓝色标出)砍掉环上的非树边和除非树边外的任意一边,就可以把图分为两部分。
如果有多个非树边(用橙色表示):
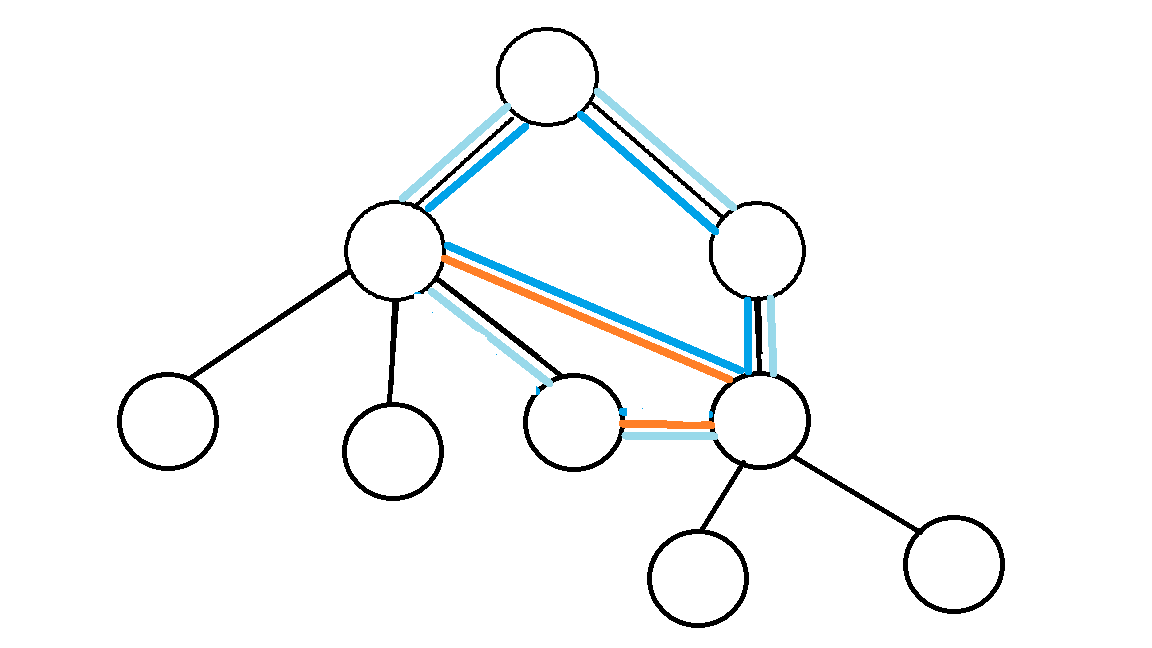
同属于多个非树边构成环的边,是不符合题目要求的。
所以可以计算有多少条边最终只被非树边覆盖小于2次,得到答案。
如果被覆盖1次:那么贡献一种方案;
如果被覆盖0次:那么贡献\(m\)种方案
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=6e5+105;
int n,m,mod,ans;
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*f;
}
//-----------------------------
int to[N<<1],nex[N<<1],h[N],cnt;
inline void add(int x,int y){
to[++cnt]=y;
nex[cnt]=h[x];h[x]=cnt;
}
int d[N],f[N][25];
//----------------------------
void bfs(int x){
queue<int> q;q.push(1);d[1]=1;
while(!q.empty()){
int x=q.front();q.pop();
for(int i=h[x];i;i=nex[i]){
int y=to[i];
if(d[y]) continue;
d[y]=d[x]+1;f[y][0]=x;
for(int j=1;j<=23;j++)f[y][j]=f[f[y][j-1]][j-1];
q.push(y);
}
}
}
inline int lca(int x,int y){
if(d[x]>d[y]) swap(x,y);
for(int i=23;i>=0;i--) if(d[f[y][i]]>=d[x]) y=f[y][i];
if(x==y) return x;
for(int i=23;i>=0;i--)if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
return f[x][0];
}
//--------------------------------
bool v[N];
int s[N];
inline void dfs(int x){
v[x]=1;
for(int i=h[x];i;i=nex[i]){
int y=to[i];
if(v[y]) continue;
dfs(y);
s[x]+=s[y];
}
}
signed main(){
n=read();m=read();
for(int i=1,x,y;i<n;i++){
x=read();y=read();
add(x,y);add(y,x);
}
bfs(1);
for(int i=1,x,y;i<=m;i++){
x=read();y=read();
s[x]++;s[y]++;
s[lca(x,y)]-=2;
}
dfs(1);
for(int i=2;i<=n;i++){
if(!s[i]) ans+=m;
if(s[i]==1) ans+=1;
}
printf("%lld",ans);
return 0;
}
T6 【2018.8雅礼8.13T1】d
题目
描述
给定 \(n\) 个边平行于坐标轴的矩形,长宽分别为 \(a_i、b_i\) 。
你可以任意平移矩形,删除至多 \(m\) 个矩形,但不允许旋转它们。
问最后所有剩余矩形的交的面积最大是多少。
输入格式
第一行,一个自然数 \(T\),代表数据组数。
对于每组数据:
第一行,一个正整数 \(n\),一个自然数 \(m\)。
接下来 \(n\) 行,每行两个正整数,\(a_i,b_i\)。
思路
最大化 \(min\) \({a_i}\) \(× min\) \({b_i}\),贪心选择若干个 \(a_i\) 最小的矩形和若干个\(b_i\)最小的矩形删除·。
枚举删除几个\(a_i\)最小的矩形,剩下的删除\(b_i\)最小的矩形,用排序预处理\(min\) \(a_i\),用堆维护 \(min\) \(b_i\)。
code
#include<bits/stdc++.h>
#define re register
#define int long long
#define ll long long
using namespace std;
const int N=1e6+105;
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*f;
}
struct qwq{int a,b;}q[N];
bool cmp(qwq x,qwq y){return x.a<y.a;}
int T,m,n;
ll ans;
signed main(){
T=read();
while(T--){
n=read();m=read();
for(re int i=1;i<=n;i++){q[i].a=read();q[i].b=read();}
sort(q+1,q+1+n,cmp);
priority_queue<int,vector<int> ,greater<int> > pwp;
for(re int i=m+1;i<=n;i++)pwp.push(q[i].b);
ans=q[m+1].a*pwp.top();
for(re int i=m;i;i--){
pwp.push(q[i].b);pwp.pop();
ll x=q[i].a*pwp.top();
if(ans<x) ans=x;
}
printf("%lld\n",ans);
}
return 0;
}
其他题目见 近期模拟赛2

 最近考试的题目
最近考试的题目

 浙公网安备 33010602011771号
浙公网安备 33010602011771号