矩阵加速递推
矩阵乘法，矩阵快速幂，矩阵加速递推
前言
几天前：
某人 ：这个题搞一下矩阵就好。
我 ： ？
某人 ：矩阵啊！先推式子，然后搞个矩阵快速幂 。
我 ：？
某人 ：你不会矩阵？开玩笑吧，你学了个啥？
我 ：不不不，矩阵乘法我还是知道的。
某人：但凡你花几分钟……来，你康康这个。
几分钟后
我 ：谢谢，我会了，我可以！
……
考试的时候式子一下就推出来了，然后写挂了。
100 ——> 30
难受
矩阵快速幂
矩阵乘法：
（由于会latex的巨佬回家打疫苗去了，所以我只能用画图拿鼠标写了
矩阵乘法的公式是：
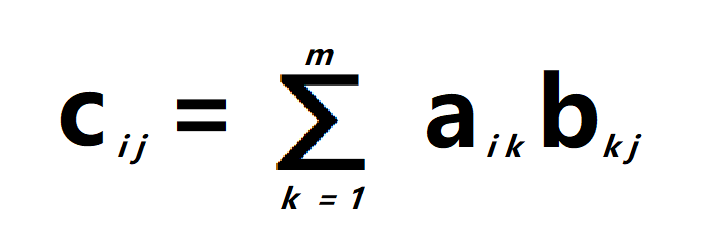
文字解释即：结果的第 \(i\) 行 \(j\) 列等于 用前一个矩阵的第 \(i\) 行 乘 后一个矩阵的第 \(j\) 列 （的对应数）各项再做和
其中，因为矩阵乘法要求前一个矩阵的列数与后一个矩阵的行数相同，即：前者为\(N_A × M\) ，后者为 \(M×N_B\)。最后得到的结果矩阵为\(N_A×N_B\)
用 \(a_{ij}\)表示，矩阵A的第\(i\)行第\(j\)列的数
举个例子：
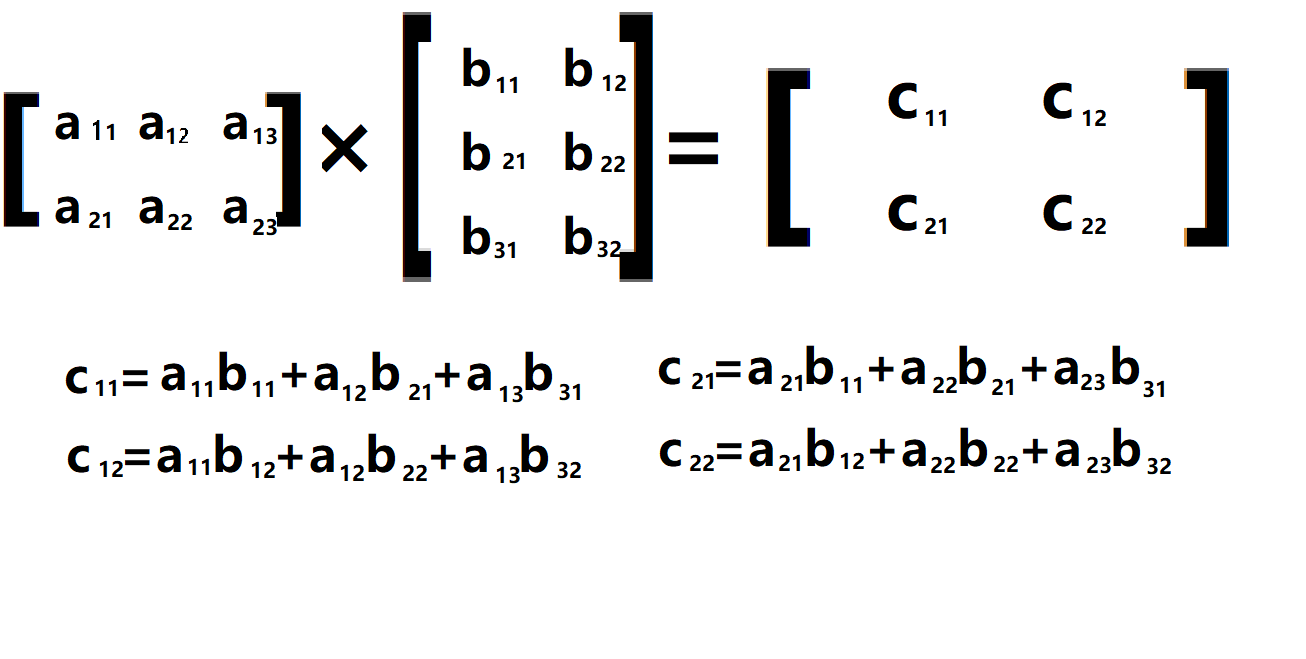
快速幂
求 \(a^b\) $ mod $ \(p\)
普通快速幂有两种操作：
1.和答案乘
if(b&1) ans=ans*a%p;
- 自乘
a=a*a%p;
矩阵快速幂同理，但是要处理矩阵乘法，也就是，不是一个"\(*\)"号就可以。
假设矩阵是\(n×n\)的（也只有这样的矩阵能够自乘
那么根据公式就有：
\((1)\) 自乘：
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
for(int k=1;k<=n;k++)
b[i][j]+=a[i][k]*a[k][j];
//先用b数组暂存新的a
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
a[i][j]=b[i][j];
//把数值赋值回去
\((2)\) 和答案矩阵乘：
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
for(int k=1;k<=n;k++)
b[i][j]+=a[i][k]*c[k][j];
//暂存
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
c[i][j]=b[i][j];
//赋值
最后不能忘记 \(mod\) \(p\) ，和清 \(b\) 数组。
code
水哥struct版
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int mod=1e9+7;
ll n,k;
struct matrix{
ll A[115][115];
inline void init(){memset(A,0,sizeof(A));}
inline ll* operator [] (const int k){return A[k];}
inline matrix operator *(matrix &B){
matrix res;res.init();
for(int i=0;i<n;i++)for(int j=0;j<n;j++)for(int t=0;t<n;t++)
res[i][j]=(res[i][j]+A[i][t]*B[t][j])%mod;
return res;
}
inline matrix ksm(ll x){
matrix res;res.init();matrix tmp=*this;
for(int i=0;i<n;i++) res[i][i]=1;
while(x){
if(x&1) res=res*tmp;
tmp=tmp*tmp;x>>=1;
}
return res;
}
}MAP;
int main(){
scanf("%lld%lld",&n,&k);
for(int i=0;i<n;i++)for(int j=0;j<n;j++)scanf("%lld",&MAP[i][j]);
MAP=MAP.ksm(k);
for(int i=0;i<n;i++){
for(int j=0;j<n;j++) printf("%lld ",MAP[i][j]);
putchar('\n');
}
return 0;
}
朴素版：
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=205;
const int mod=1e9+7;
int n,k,a[N][N],b[N][N],c[N][N];
inline void c1(){//自乘
memset(b,0,sizeof(b));
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
for(int k=1;k<=n;k++)
b[i][j]=(b[i][j]+a[i][k]*a[k][j])%mod;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
a[i][j]=b[i][j];
}
inline void c2(){//答案乘
memset(b,0,sizeof(b));
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
for(int k=1;k<=n;k++)
b[i][j]=(b[i][j]+c[i][k]*a[k][j])%mod;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
c[i][j]=b[i][j];
}
void ksm(int b){
for(int i=1;i<=n;i++)c[i][i]=1;//单位矩阵，等价于：int ans=1;
while(b){
if(b&1)c2();
b>>=1;c1();
}
}
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*f;
}
signed main(){
n=read();k=read();
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
a[i][j]=read();
ksm(k);
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++)printf("%lld ",c[i][j]);
printf("\n");
}
return 0;
}
此外，今天教练找我聊天了，超级开心，决定放出自己的正常码风的代码：
舒适版：
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=205,mod=1e9+7;
int n,k,a[N][N],b[N][N],c[N][N];
inline void c1(){//自乘
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)for(int k=1;k<=n;k++)b[i][j]=(b[i][j]+a[i][k]*a[k][j])%mod;
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)a[i][j]=b[i][j];
}
inline void c2(){//答案乘
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)for(int k=1;k<=n;k++)b[i][j]=(b[i][j]+c[i][k]*a[k][j])%mod;
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)c[i][j]=b[i][j];
}
void ksm(int k){
for(int i=1;i<=n;i++)c[i][i]=1;//单位矩阵，等价于：int ans=1;
while(k){if(k&1){memset(b,0,sizeof(b));c2();}k>>=1;memset(b,0,sizeof(b));c1();}
}
inline int read(){int x=0,f=1;char ch=getchar();while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}return x*f;}
signed main(){
n=read();k=read();
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)a[i][j]=read();
ksm(k);
for(int i=1;i<=n;i++){for(int j=1;j<=n;j++)printf("%lld ",c[i][j]);printf("\n");}
return 0;
}
矩阵加速递推
斐波那契数列
题意：求斐波那契数列第\(n\)项。
斐波那契数列：规定， \(f(n) = f(n-1) + f(n-2)\) \(（ n ≥ 3 ）\) ，且 \(f(1)=1,f(2)=1\)
假设有这样一个矩阵 \(A\) ,使得：
\[\begin{bmatrix}
f(n-1) & f(n-2)
\end{bmatrix} \times A= \begin{bmatrix}
f(n) & f(n-1)
\end{bmatrix}
\]
那么就可以有：
\[\begin{bmatrix}
f(2) & f(1)
\end{bmatrix}\times A^{n-2}= \begin{bmatrix}
f(n) & f(n-1)
\end{bmatrix}
\]
那么重点就变成了怎么求 \(A\)
\[\begin{bmatrix}
f(n-1) & f(n-2)
\end{bmatrix} \times A= \begin{bmatrix}
f(n) & f(n-1)
\end{bmatrix}
\]
\(f(n) = f(n-1) + f(n-2)\) \(（ n ≥ 3 ）\)
从这两个式子下手。
首先，因为 \(f(n) = f(n-1) + f(n-2)\) ，所以结果矩阵 \(（1,1）\) 是由两者做和得到的。根据矩阵乘法的规定，首先得知\(A\)是一个\(2×2\)的矩阵。又根据公式：
$C_{1,1} =f(n)=f(n-1) × A_{1,1} + f(n-2) + × A_{2,1} $
$C_{1,2}=f(n-1)=f(n-1) × A_{1,2} + f(n-2) × A_{2,2} $
所以，容易得到：
\[A= \begin{bmatrix}
1 & 1\\
1 & 0
\end{bmatrix}
\]
最后只需要求 \(A^{n-2}\) 再算一次矩阵乘法即可。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=205;
const int mod=1e9+7;
int n,k,a[N][N],b[N][N],c[N][N];
inline void c1(){
memset(b,0,sizeof(b));
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
for(int k=1;k<=n;k++)
b[i][j]=(b[i][j]+a[i][k]*a[k][j])%mod;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
a[i][j]=b[i][j];
}
inline void c2(){
memset(b,0,sizeof(b));
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
for(int k=1;k<=n;k++)
b[i][j]=(b[i][j]+c[i][k]*a[k][j])%mod;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
c[i][j]=b[i][j];
}
void ksm(int b){
for(int i=1;i<=n;i++)c[i][i]=1;
while(b){
if(b&1)c2();
b>>=1;c1();
}
}
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*f;
}
signed main(){
k=read();n=2;
if(k==1 || k==2){printf("1");return 0;}//注意特判，不然会T
a[1][1]=1;a[1][2]=1;a[2][1]=1;a[2][2]=0;
int f[1][2];f[1][1]=1;f[1][2]=1;
ksm(k-2);
memset(b,0,sizeof(b));
for(int j=1;j<=2;j++)
for(int k=1;k<=2;k++)
b[1][j]=(b[1][j]+f[1][k]*c[k][j])%mod;
printf("%lld",b[1][1]);
return 0;
}
bigger,better,stronger
来一道差不多的 考试 题
题意：
下面数列的第 \(n\) 项：
\(f(0) = a_0 ,f(1) = a_1 ,f(2) = a_2\)
\(f(n) = b × f(n − 1) + c × f(n − 2) + d × f(n − 3) + e\) \((n ≥ 3)\)
给出 \(a_0,a_1,a_2,b,c,d,e,n\) 求第\(n\)项
解
同样的思路
\[\begin{bmatrix}
f(n-1) & f(n-2) & f(n-3) & e
\end{bmatrix}\times A = \begin{bmatrix}
f(n) & f(n-1) & f(n-2) & e
\end{bmatrix}
\]
先得到\(A\)是一个\(4×4\)的矩阵，再联立得到式子：
\[C_{1,1}=f(n)=f(n-1)×A_{1,1}+f(n-2)×A_{2,1}×f(n-3)×A_{3,1}+e×A_{4,1}
\]
\[f(n) = b × f(n − 1) + c × f(n − 2) + d × f(n − 3) + e
\]
\[\therefore A_{1,1}=b , A_{2,1}=c , A_{3,1}=d , A_{4,1}=1
\]
\[C_{1,2}=f(n-1)=f(n-1)×A_{1,2}+f(n-2)×A_{2,2}×f(n-3)×A_{3,2}+e×A_{4,2}
\]
\[\therefore A_{1,2}=1 , A_{2,2}=0 , A_{3,2}=0 , A_{4,2}=0
\]
同理可得：
\[\therefore A_{1,3}=0 , A_{2,3}=1 , A_{3,3}=0 , A_{4,3}=0
\]
\[\therefore A_{1,4}=0 , A_{2,4}=0 , A_{3,4}=0 , A_{4,4}=1
\]
所以\(A\)长这样：
\[A=\begin{bmatrix}
b & 1 & 0 & 0\\
c & 0 & 1 & 0\\
d & 0 & 0 & 0\\
1 & 0 & 0 & 1
\end{bmatrix}
\]
code
座右铭：我从来没有见过这样阴郁而又光明的日子。
