动态规划
树形DP
没有上司的舞会
题意
有一个有\(n+1\)个节点的树,树根为 \(0\)。编号为 $ 1到n $ 的点分别有自己的权值\(r_i\)。在\(1到n\)的节点中,如果取了一个节点的父亲节点,那么就不能取这个节点。
求总权值的最大值。
解
设 \(dp[i][0/1]\) 为以\(i\)为根的子树,取 / 不取 \(i\) 所得的权值最大值。
所以答案 $ =max(dp[0][1],dp[0][0]) $ .
用 \(s_i\) 表示 \(i\) 的孩子的集合,用 \(val[i]\) 表示节点 \(i\) 的权值。
那么状态转移:
如果不选\(i\):
\(dp[i][0]=\sum_{j∈s_i}^{} max(dp[j][0],dp[j][1])\)
如果选\(i\):
$dp[i][1]=( \sum_{j∈s_i} dp[j][0] ) + val[i] $
关于循环方式:\(dfs\)
code
#include<bits/stdc++.h>
using namespace std;
const int N=6e4+105;
int dp[N][3];
int nex[N],to[N],v[N],h[N];bool f[N];
int n,x,y,z,root,cnt;
inline void add(int x,int y){to[++cnt]=y;nex[cnt]=h[x];h[x]=cnt;}
void dfs(int x){
f[x]=1;dp[x][1]=v[x];
for(int i=h[x];i;i=nex[i]){
if(f[to[i]])continue;
dfs(to[i]);
dp[x][1]+=dp[to[i]][0];
dp[x][0]+=max(dp[to[i]][1],dp[to[i]][0]);
}
}
int main(){
cin>>n;
for(int i=1;i<=n;i++)cin>>v[i];
for(int i=1;i<n;i++){
cin>>x>>y;
add(x,y);add(y,x);
}
dfs(1);
printf("%d",max(dp[1][0],dp[1][1]));
return 0;
}
最大子树和
题意
找到树上点权之和最大的一个连通分量。(虽然原题说了很多,但是总结起来确实只有这句话
解
设 \(dp[i]\) 为 以\(i\)为根的子树中的最大点权和
所以有:
\(dp[i]=v[i]+( dp [j] > 0 ? dp [j] : 0 )\) ,
\(j为i的儿子\)
code
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+105;
const int INF=2147483647;
int dp[N],n,x,y,ans=-INF;
int nex[N],to[N],h[N],v[N],cnt;bool f[N];
void add(int x,int y){to[++cnt]=y;nex[cnt]=h[x];h[x]=cnt;}
void dfs(int x){
dp[x]=v[x];f[x]=1;
for(int i=h[x];i;i=nex[i]){
if(f[to[i]])continue;
dfs(to[i]);
dp[x]+=((dp[to[i]]>0)?dp[to[i]]:0);
}
}
int main(){
cin>>n;
for(int i=1;i<=n;i++)cin>>v[i];
for(int i=1;i<n;i++){
cin>>x>>y;
add(x,y);add(y,x);
}
dfs(1);
for(int i=1;i<=n;i++)ans=max(ans,dp[i]);
printf("%d",ans);
return 0;
}
[CTSC1997]选课
题意
树形背包模板。
有一个有 \(N\) 个节点的森林,取一个节点的权值时,要求也要取其父亲节点。一共取\(M\)个点。
解
把所有树的根节点连接一个 \(0\) 节点,变成一棵树。
在树上跑背包。
code
#include<bits/stdc++.h>
using namespace std;
const int N=405;
int nex[N],to[N],v[N],h[N],cnt;
int dp[N][N],root,n,m,x,y;
inline void add(int x,int y){to[++cnt]=y;nex[cnt]=h[x];h[x]=cnt;}
void dfs(int x,int w){
if(m<=0) return ;
for(int i=h[x];i;i=nex[i]){
for(int k=0;k<w;k++) dp[to[i]][k]=dp[x][k]+v[to[i]];
dfs(to[i],w-1);
for(int k=1;k<=w;k++)dp[x][k]=max(dp[x][k],dp[to[i]][k-1]);
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>x>>v[i];
add(x,i);
}
dfs(0,m);
printf("%d",dp[0][m]);
return 0;
}
送给好友的礼物
考试题
题意:
给定一棵包含 \(n\) 个结点的树 \(T\),结点从 \(1 到 n\) 顺序编号。
小 \(M\) 和小 \(B\) 在时刻 \(0\) 都在 \(1\) 号结点。从时刻 \(1\) 开始的每个时刻初,小 \(M\) 和小 \(B\) 都可以选择:移动到一个和自己所在结点直接相连的结点,或者停留在当前所在的结点。
树上有 \(k\) 个草莓,它们分布在 \(k\) 个不同的结点上。小 \(M\) 和小 \(B\) 想要收集到所有的草莓,任何一个时刻末,如果小 \(M\) 或者小 \(B\) 在某一个草莓所在的结点上,那么这个草莓就被收集了。
她们不想花费太多的时间,因此你需要回答:至少在第几时刻末,小 \(M\) 和小 \(B\) 可以收集到所有的草莓,并且都回到结点 \(1\)。
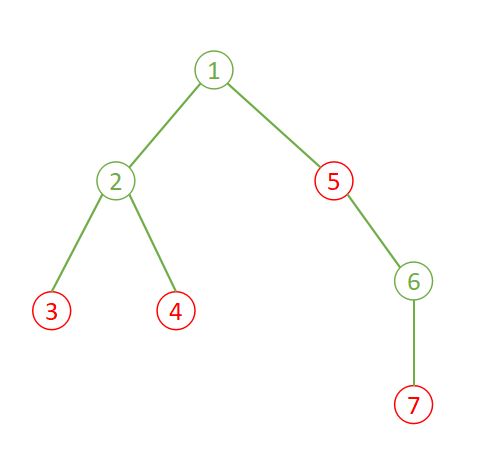
样例
\(输入\)
\(7\) \(4\)
\(1\) \(2\)
\(2\) \(3\)
\(2\) \(4\)
\(1\) \(5\)
\(5\) \(6\)
\(6\) \(7\)
\(3\) \(4\) \(5\) \(7\)
\(输出\)
\(6\)
解
其实我觉得搞玄学也不是不行……
首先把一些没有草莓的子树砍掉。那么叶子节点就都是草莓了。
所以就是需要遍历整棵树。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1000;
const int INF=2147483647;
int n,k;
int cnt,h[N],nex[N<<1],to[N<<1];
int f[N],siz[N],dp[N][N<<1];
bool vis[N];
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*f;
}
void add(int x,int y){to[++cnt]=y;nex[cnt]=h[x];h[x]=cnt;}
bool dfs(int x){
bool fs=0;
for(int i=h[x];i;i=nex[i]){
int y=to[i];
if(y==f[x] || !y) continue;
f[y]=x;bool now=dfs(y);
if(!now)to[i]=0;
fs|=now;
}
return fs|vis[x];
}
void work(int x){
siz[x]=1;dp[x][0]=0;
for(int k=h[x];k;k=nex[k]){
int y=to[k];
if(y==f[x]||!y)continue;
work(y);siz[x]+=siz[y];
for(int i=(siz[x]-1)*2;i>=0;i--){
dp[x][i]=dp[x][i]+dp[y][0]+2;
if(i>=siz[y]*2)
{dp[x][i]=min(dp[x][i],dp[x][i-siz[y]*2]+dp[y][(siz[y]-1)*2]);}
for(int j=min((siz[y]-1)*2,i-2);j>=0;j--)
{dp[x][i]=min(dp[x][i],dp[x][i-j-2]+dp[y][j]+2);}
}
}
}
int main(){
memset(dp,0x3f,sizeof(dp));
n=read();k=read();
for(int i=1;i<n;i++){
int x=read(),y=read();
add(x,y);add(y,x);
}
for(int i=1;i<=k;i++)vis[read()]=1;
dfs(1);work(1);
int ans=INF;
for(int i=0;i<=(siz[1]-1)*2;i++)ans=min(ans,max(i,dp[1][i]));
printf("%d",ans);
return 0;
}
区间DP
[NOI1995] 石子合并
题目描述
在一个圆形操场的四周摆放 \(N\) 堆石子,现要将石子有次序地合并成一堆.规定每次只能选 相邻的 \(2\) 堆 合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分。
试设计出一个算法,计算出将 \(N\) 堆石子合并成 \(1\) 堆的最小得分和最大得分。
code
#include<bits/stdc++.h>
using namespace std;
const int N=305;
const int INF=2147483640;
int a[N],q[N],n,dp1[N][N],dp2[N][N];
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*f;
}
int main(){
n=read();
memset(dp1,0x3f,sizeof(dp1));memset(dp2,0x80,sizeof(dp2));
int m=n*2;
for(int i=1;i<=m;i++)dp1[i][i]=0,dp2[i][i]=0;
for(int i=1;i<=n;i++){a[i]=read();a[i+n]=a[i];}
for(int i=1;i<=m;i++) q[i]=a[i]+q[i-1];
for(int len=2;len<=n;len++)
for(int l=1;l<=m;l++){
int r=l+len-1;
if(r>m) break;
for(int k=l;k<r;k++){
dp1[l][r]=min(dp1[l][k]+dp1[k+1][r]+q[r]-q[l-1],dp1[l][r]);
dp2[l][r]=max(dp2[l][k]+dp2[k+1][r]+q[r]-q[l-1],dp2[l][r]);
}
}
int ans1=INF,ans2=(-INF);
for(int i=1;i<=n;i++){
ans1=min(ans1,dp1[i][i+n-1]);
ans2=max(ans2,dp2[i][i+n-1]);
}
printf("%d\n%d",ans1,ans2);
return 0;
}
[NOIP2006 提高组] 能量项链
题目描述
在 Mars 星球上,每个 Mars 人都随身佩带着一串能量项链。在项链上有 NN 颗能量珠。能量珠是一颗有头标记与尾标记的珠子,这些标记对应着某个正整数。并且,对于相邻的两颗珠子,前一颗珠子的尾标记一定等于后一颗珠子的头标记。因为只有这样,通过吸盘(吸盘是 Mars 人吸收能量的一种器官)的作用,这两颗珠子才能聚合成一颗珠子,同时释放出可以被吸盘吸收的能量。如果前一颗能量珠的头标记为 mm,尾标记为 rr,后一颗能量珠的头标记为 rr,尾标记为 nn,则聚合后释放的能量为 m \times r \times nm×r×n(Mars 单位),新产生的珠子的头标记为 mm,尾标记为 nn。
需要时,Mars 人就用吸盘夹住相邻的两颗珠子,通过聚合得到能量,直到项链上只剩下一颗珠子为止。显然,不同的聚合顺序得到的总能量是不同的,请你设计一个聚合顺序,使一串项链释放出的总能量最大。
例如:设 N=4N=4,44 颗珠子的头标记与尾标记依次为 (2,3)(3,5)(5,10)(10,2)(2,3)(3,5)(5,10)(10,2)。我们用记号 \oplus⊕ 表示两颗珠子的聚合操作,(j \oplus k)(j⊕k) 表示第 j,kj,k 两颗珠子聚合后所释放的能量。则第 44 、 11 两颗珠子聚合后释放的能量为:
(4 \oplus 1)=10 \times 2 \times 3=60(4⊕1)=10×2×3=60。
这一串项链可以得到最优值的一个聚合顺序所释放的总能量为:
((4 \oplus 1) \oplus 2) \oplus 3)=10 \times 2 \times 3+10 \times 3 \times 5+10 \times 5 \times 10=710((4⊕1)⊕2)⊕3)=10×2×3+10×3×5+10×5×10=710。
输入格式
第一行是一个正整数 N(4 \le N \le 100)N(4≤N≤100),表示项链上珠子的个数。第二行是 NN 个用空格隔开的正整数,所有的数均不超过 10001000。第 ii 个数为第 ii 颗珠子的头标记 (1 \le i \le N)(1≤i≤N),当 i<Ni<N 时,第 ii 颗珠子的尾标记应该等于第 i+1i+1 颗珠子的头标记。第 NN 颗珠子的尾标记应该等于第 11 颗珠子的头标记。
至于珠子的顺序,你可以这样确定:将项链放到桌面上,不要出现交叉,随意指定第一颗珠子,然后按顺时针方向确定其他珠子的顺序。
普通的背包
(1) 01背包问题
P2871 [USACO07DEC]Charm Bracelet S
题目
有 \(N\) 件物品和一个容量是 \(M\) 的背包。每件物品只能使用一次。
第 \(i\) 件物品的重量是 \(C_i\),价值是 \(W_i\) 。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入
第一行:物品个数 \(N\) 和背包大小 \(M\)
第二行至第 \(N+1\) 行:第 \(i\) 个物品的重量 \(C_i\) 和价值 \(W_i\)
code
注释版:
#include<bits/stdc++.h>
using namespace std;
const int maxn=5e3+105;//注意空间大小
int N,M,c[maxn],w[maxn],f[maxn][maxn];
int main(){
//cout<<"Nickle's code"<<endl;
cin>>N>>M;//N为物品个数,M为背包大小
for(int i=1;i<=N;i++) cin>>c[i]>>w[i];//c为重量,w为价值
for(int i=1;i<=N;i++)
for(int j=M;j>=0;j--){
if(j>=c[i]) f[i][j]=max(f[i-1][j-c[i]]+w[i],f[i-1][j]);
else f[i][j]=f[i-1][j];
}
cout<<f[N][M];
return 0;
}
核心代码纯享版:
for(int i=1;i<=N;i++)
for(int j=M;j>=0;j--){
if(j>=c[i]) f[i][j]=max(f[i-1][j-c[i]]+w[i],f[i-1][j]);
else f[i][j]=f[i-1][j];
}
cout<<f[N][M];
(2) 分组(01)背包
题目描述
自 \(01\) 背包问世之后,小 \(A\) 对此深感兴趣。
一天,小 \(A\) 去远游,却发现他的背包不同于 \(01\) 背包,他的物品大致可分为 \(k\) 组,每组中的物品相互冲突,现在,他想知道最大的利用价值是多少。
输入格式
两个数 \(m,n\) ,表示一共有 \(n\) 件物品,总质量为 \(m\)
接下来 \(n\) 行,每行 \(3\) 个数 \(a_i,b_i,c_i\) 表示物品的重量,利用价值,所属组数
code
注释:
#include<bits/stdc++.h>
using namespace std;
const int maxn=5e3+105;//注意空间大小
int m,n,f[maxn],a[maxn],b[maxn],Kind,c_cnt[1005],c_num[1005][1005],x;
//kind记录组数,f是转移数组,a是重量,b是价值
//c_cnt[i]记录第i组一共有几件东西,c_num[i][j]记录第i组第j件物品的总序号
int main(){
//cout<<"Nickle"'s code"<<endl;
cin>>m>>n;
for(int i=1;i<=n;i++){
cin>>a[i]>>b[i]>>x;
Kind=max(x,Kind);
c_cnt[x]++;c_num[x][c_cnt[x]]=i;
}
for(int i=1;i<=Kind;i++)
for(int j=m;j>=0;j--)
for(int k=1;k<=c_cnt[i];k++)
if(j>=a[c_num[i][k]])f[j]=max(f[j],f[j-a[c_num[i][k]]]+b[c_num[i][k]]);
cout<<f[m];
return 0;
}
核心代码:
for(int i=1;i<=Kind;i++)
for(int j=m;j>=0;j--)
for(int k=1;k<=c_cnt[i];k++)
if(j>=a[c_num[i][k]])f[j]=max(f[j],f[j-a[c_num[i][k]]]+b[c_num[i][k]]);
(3) 完全背包问题
题目
有 \(N\) 种物品和一个容量是 \(V\) 的背包,每种物品都有无限件可用。第 \(i\) 种物品的体积是 \(v_i\),价值是 \(w_i\) 。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。输出最大价值。
输入格式
第一行两个整数,\(N\),\(V\),用空格隔开,分别表示物品种数和背包容积。
接下来有 \(N\) 行,每行两个整数 \(v_i,w_i\),用空格隔开,分别表示第 \(i\) 种物品的体积和价值。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e7+5;
int n,V,w[N],v[N],f[N];
signed main(){
cin>>n>>V;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
for(int i=1;i<=n;i++)
for(int j=v[i];j<=V;j++)
f[j]=max(f[j],f[j-v[i]]+w[i]);
cout<<f[V];
return 0;
}
核心代码:
for(int i=1;i<=n;i++)
for(int j=v[i];j<=V;j++)
f[j]=max(f[j],f[j-v[i]]+w[i]);
(4) 多重背包问题
问题一
题目
有 \(N\) 种物品和一个容量是 \(V\) 的背包。
第 \(i\) 种物品最多有 \(s_i\) 件,每件体积是 \(v_i\),价值是 \(w_i\)。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。输出最大价值。
输入格式
第一行两个整数,N,V,
用空格隔开,分别表示物品种数和背包容积。
接下来有 N 行,每行三个整数 vi,wi,si,
用空格隔开,分别表示第 i 种物品的体积、价值和数量。
code
#include<bits/stdc++.h>
using namespace std;
const int m=1e4+5;
int T,M,num,val,wight,cnt,tot,w[m],v[m],f[m];
int main(){
cin>>M>>T;
while(M--){
cin>>wight>>val>>num;
while(num--){v[++cnt]=val;w[cnt]=wight;}
}
for(int i=1;i<=cnt;i++)for(int j=T;j>=w[i];j--)f[j]=max(f[j],f[j-w[i]]+v[i]);
cout<<f[T];
return 0;
}
核心代码
while(num--){v[++cnt]=val;w[cnt]=wight;}
问题二 二进制优化方法
给定任意一个数\(s\),最少把\(s\)分为多少个数,可以使得这些数拼成小于等于\(s\)的所有数?
\(log2(s)\)
假设这个数是\(8\),可以拆成\(1,2,4\)
假设这个数是\(10\),可以拆成\(1,2,4,3\)
假设这个数是\(7\),可以拆成\(1,2,4\)
\(s-1-2-4……\)一直到不能减为止
code
#include<bits/stdc++.h>
using namespace std;
int n,m,f[2105],v,w,s;
struct qwq{int v,w;};
vector<qwq> q;
int main(){
cin>>n>>m;
for(int i=0;i<n;i++){
cin>>v>>w>>s;
for(int k=1;k<=s;k<<=1){s-=k;q.push_back({v*k,w*k});}
if(s>0) q.push_back({v*s,w*s});
}
for(auto qwq: q)for(int j=m;j>=qwq.v;j--)f[j]=max(f[j],f[j-qwq.v]+qwq.w);
cout<<f[m]<<endl;
return 0;
}
问题三 单调队列优化
code
#include<bits/stdc++.h>
using namespace std;
const int N=2e4+105;
int n,m,f[N],g[N],q[N],c,w,s;
int main(){
cin>>n>>m;
for(int i=0;i<n;i++){
cin>>c>>w>>s;
memcpy(g,f,sizeof(f));
for(int j=0;j<c;j++){
int hh=0,tt=-1;
for(int k=j;k<=m;k+=c){
f[k]=g[k];
if(hh<=tt&&k-s*c>q[hh]) hh++;
if(hh<=tt) f[k]=max(f[k],g[q[hh]]+(k-q[hh])/c*w);
while(hh<=tt&&g[q[tt]]-(q[tt]-j)/c*w<=g[k]-(k-j)/c*w) tt--;
q[++tt]=k;
}
}
}
cout<<f[m];
return 0;
}
没有auto的代码:
#include<bits/stdc++.h>
using namespace std;
const int N=1e4+105,M=2e3+105;
int n,m,v[N],w[N],f[N],cnt,a,b,s;
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a>>b>>s;
int k=1;
while(k<=s){v[++cnt]=a*k;w[cnt]=b*k;s-=k;k<<=1;}
if(s>0){v[++cnt]=a*s;w[cnt]=b*s;}
}
for(int i=1;i<=cnt;i++)for(int j=m;j>=v[i];j--)f[j]=max(f[j],f[j-v[i]]+w[i]);
cout<<f[m];
return 0;
}
(5) 混合背包问题
题目
有 \(N\) 种物品和一个容量是 \(V\) 的背包。
物品一共有三类:
-
第一类物品只能用 \(1\) 次( \(01\) 背包);
-
第二类物品可以用无限次(完全背包);
-
第三类物品最多只能用 \(s_i\) 次(多重背包);
每种体积是 \(v_i\),价值是 \(w_i\) 。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。输出最大价值。
输入格式
第一行两个整数,\(N,V\),用空格隔开,分别表示物品种数和背包容积。
接下来有 \(N\) 行,每行三个整数 \(v_i,w_i,s_i\),用空格隔开,分别表示第 \(i\) 种物品的体积、价值和数量。
-
\(s_i=−1\) 表示第 \(i\) 种物品只能用 \(1\) 次;
-
\(s_i=0\) 表示第 \(i\) 种物品可以用无限次;
-
\(s_i>0\) 表示第 \(i\) 种物品可以使用 \(s_i\) 次;
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+105;
int n,m,v[N],w[N],f[N],cnt,a,b,s;
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a>>b>>s;
int k=1;
if(s<0) s=1;
else if(s==0) s=m/a;
while(k<=s){v[++cnt]=a*k;w[cnt]=b*k;s-=k;k<<=1;}
if(s>0){v[++cnt]=s*a;w[cnt]=b*s;}
}
for(int i=1;i<=cnt;i++)for(int j=m;j>=v[i];j--)f[j]=max(f[j],f[j-v[i]]+w[i]);
cout<<f[m];
return 0;
}

 树形dp
树形dp

 浙公网安备 33010602011771号
浙公网安备 33010602011771号