差分约束
负环，差分约束系统。
前言
这个算是鸽了很久都没去学的算法。然后模拟赛考出来（我又不会并查集做法），所以在改题之前，还得先完成一下前置知识。
差分约束的前置知识
<Ⅰ>\(Spfa\)判断负环
用\(Spfa\)判断入队次数是否\(≥n\)，如果是，说明有负环。感性理解一下，一个图上如果有负环，它会一直绕着负环跑，然后越来越小，越来越小……
\(code\):
#include<bits/stdc++.h>
using namespace std;
const int N=2e3+105,M=6e3+105;
int n,m,h[N],nex[M],to[M],v[M],cnt,d[N],tot[N],T,x,y,z;
bool f[N];//v已经有了
inline void add(int x,int y,int z){
to[++cnt]=y;v[cnt]=z;
nex[cnt]=h[x];h[x]=cnt;
}
bool spfa(){
memset(f,0,sizeof(f));memset(d,0x3f,sizeof(d));memset(tot,0,sizeof(tot));
queue<int>q;
d[1]=0;f[1]=1;q.push(1);
while(!q.empty()){
int x=q.front();q.pop();f[x]=0;
for(int i=h[x];i;i=nex[i])
if(d[to[i]]>d[x]+v[i]){
d[to[i]]=d[x]+v[i];
if(!f[to[i]]){
if(++tot[to[i]]>n) return 1;
q.push(to[i]);f[to[i]]=1;
}
}
}
return 0;
}
int main(){
scanf("%d",&T);
while(T--){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
scanf("%d%d%d",&x,&y,&z);
add(x,y,z);if(z>=0)add(y,x,z);
}
spfa()?puts("YES"):puts("NO");
memset(h,0,sizeof(h));cnt=0;
}
return 0;
}
<Ⅱ> 定义
差分约束系统
给出\(n\)个变量（\(x_1,x_2,x_3……x_n\)），和 \(m\) 个 约束条件 （粗略理解为不等式，求一些满足约束条件的解。
假设给出一个这样的差分约束系统：
\(x_a-x_b ≤ k_1\)
\(x_a-x_c ≤ k_2\)
\(x_b-x_d ≤ k_3\)
\(x_d-x_c ≤ k_4\)
可以把它写成统一形式： \(x_i≤x_j+k\)
转化成图，大概是这样的：
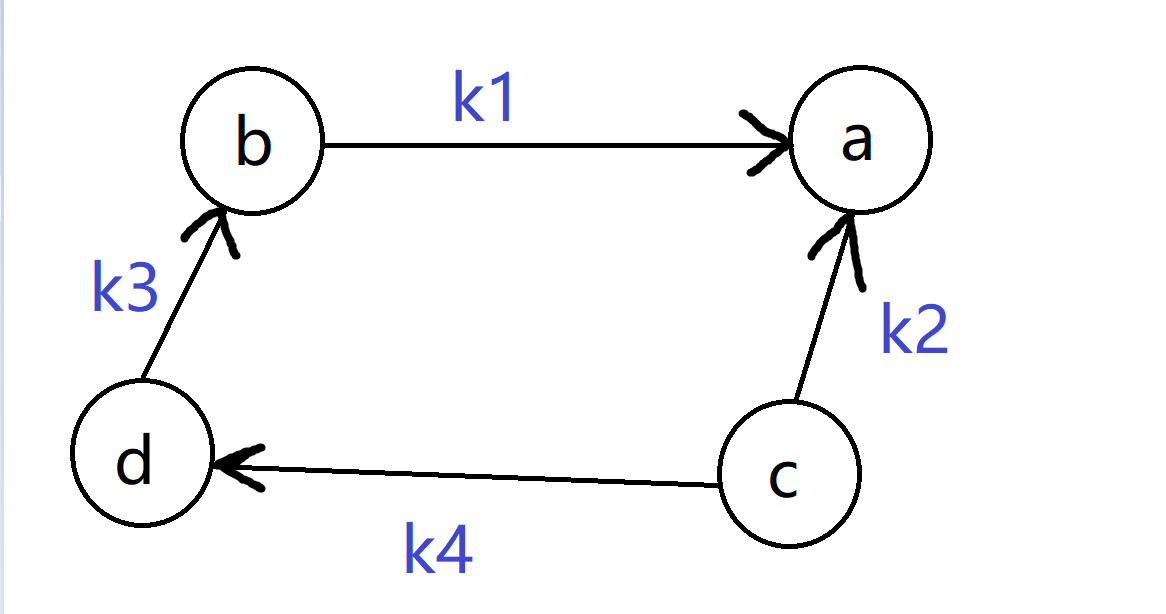
如果要找\(x_a-x_d\)的最小值，即在图上跑点\(a\)到点\(d\)的最短路。
<Ⅲ> 例题
【模板】差分约束算法
\(code\):
#include<bits/stdc++.h>
using namespace std;
const int N=2e4+105,M=6e4+105;
//变量名
int n,m,h[N],nex[M],to[M],v[M],cnt,d[N],tot[N],T,x,y,z;
bool f[N];
//建图 ,to,cnt,nex,v,h
inline void add(int x,int y,int z){
to[++cnt]=y;v[cnt]=z;
nex[cnt]=h[x];h[x]=cnt;
}
//判负环 ,f,d,tot
bool spfa(int s){
memset(f,0,sizeof(f));memset(d,0x3f,sizeof(d));memset(tot,0,sizeof(tot));
queue<int> q;
d[s]=0;f[s]=1;q.push(s);
while(!q.empty()){
int x=q.front();q.pop();f[x]=0;
for(int i=h[x];i;i=nex[i])
if(d[to[i]]>d[x]+v[i]){
d[to[i]]=d[x]+v[i];
if(!f[to[i]]){
if(++tot[to[i]]>n) return 1;//有负环->无解
q.push(to[i]);f[to[i]]=1;
}
}
}
return 0;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) add(0,i,0);
for(int i=1;i<=m;i++){
scanf("%d%d%d",&x,&y,&z);
add(y,x,z);//这里注意
}
if(spfa(0))printf("NO");
else for(int i=1;i<=n;i++)printf("%d ",d[i]);
return 0;
}
[FJOI2018]所罗门王的宝藏
题意
有一个 \(n×m\) 的矩阵，初始每个格子的权值都为 \(0\)，可以对矩阵执行两种操作：
Ⅰ 、选择一行， 该行每个格子的权值加 \(1\) 或减 \(1\)；
Ⅱ 、选择一列， 该列每个格子的权值加 \(1\) 或减 \(1\)。
现在有 \(K\) 个限制，每个限制为一个三元组 \((x,y,c)\)，代表格子 \((x,y)\) 权值等于 \(c\)。问是否存在一个操作序列，使得操作完后的矩阵满足所有的限制。如果存在输出 “\(Yes\)”，否则输出 “\(No\)”。
解
对于一个位置\((i,j)\),它的目标权值为\(c\),那么有关于第\(i\)行，第\(j\)列的值分别为\(x_i\) , \(y_j\)。可以列出一个式子：\(x_i + y_j = c\).
进一步转化：
$ => $
$ => $
再设\(y_i' = (-y_i)\).
成功转换为差分约束问题
\(code\):
#include<bits/stdc++.h>
using namespace std;
const int N=2e6+105,M=3e4+105;
//变量名
int n,m,h[N],nex[M],to[M],v[M],cnt,d[N],tot[N],T,x,y,z,k;
bool f[N];
//建图 ,to,cnt,nex,v,h
inline void add(int x,int y,int z){
to[++cnt]=y;v[cnt]=z;
nex[cnt]=h[x];h[x]=cnt;
}
//判负环 ,f,d,tot
bool spfa(int s){
memset(f,0,sizeof(f));memset(d,0x3f,sizeof(d));memset(tot,0,sizeof(tot));
queue<int> q;
d[s]=0;f[s]=1;q.push(s);
while(!q.empty()){
int x=q.front();q.pop();f[x]=0;
for(int i=h[x];i;i=nex[i])
if(d[to[i]]>d[x]+v[i]){
d[to[i]]=d[x]+v[i];
if(!f[to[i]]){
if(++tot[to[i]]>n+m) return 1;//有负环->无解
q.push(to[i]);f[to[i]]=1;
}
}
}
return 0;
}
int main(){
scanf("%d",&T);
while(T--){
memset(h,0,sizeof(h));memset(tot,0,sizeof(tot));memset(v,0,sizeof(v));
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=n+m;i++)add(0,i,0);
for(int i=1;i<=k;i++){
scanf("%d%d%d",&x,&y,&z);
add(x,y+n,z);add(y+n,x,-z);
}
spfa(0)?printf("No\n"):printf("Yes\n");
}
return 0;
}
