线段树优化建图
线段树优化建图，最短路
前言
今天我打开考试题目一看，发现四道考试题甚至看不出来是什么算法。
于是我听大佬说，这个题啊，是线段树优化建图板子题。很毒瘤的，不搞线段树优化建图就会爆\(0\)。
我害怕极了，自从我打暴力的水平提高，模拟退火用得越发熟练，玄学预估答案越发准确，我就没爆\(0\)过了。（至少有20分吧
所以我赶紧开始现学线段树优化建图，希望能在四个小时内学会模板
原理
结合着线段树优化建图模板题来说
题意：
有一个n个节点的有向有权图，现在给出三个类型的边：
- 从\(u\)到\(v\)的一条边权为\(w\)的边
- 从\(u\)到区间\([l,r]\)任意一点，都有权值为\(w\)的边
- 从区间\([l,r]\)任意一点到\(u\)，都有权值为\(w\)的边。
简单来说，即单点到单点，单点到区间，区间到单点。
要求求出\(1\)到其他所有边点的最短路。
首先最短路好想，直接上\(dij\)。（我不太会\(spfa\)，但我估计这题不太能用\(spfa\)）
难的是建图。如果直接暴力建图，真的直接每个点都向整个区间连边的话，空间是不够的
然后就有了线段树优化建图。
出树和入树
假设节点数量为\(3\),单点 \(3\) 向\([2,3]\)连边，权值为\(17\)。
那么建图应该是这样的：
初始图：
在还没有加边的时候，是这样的：
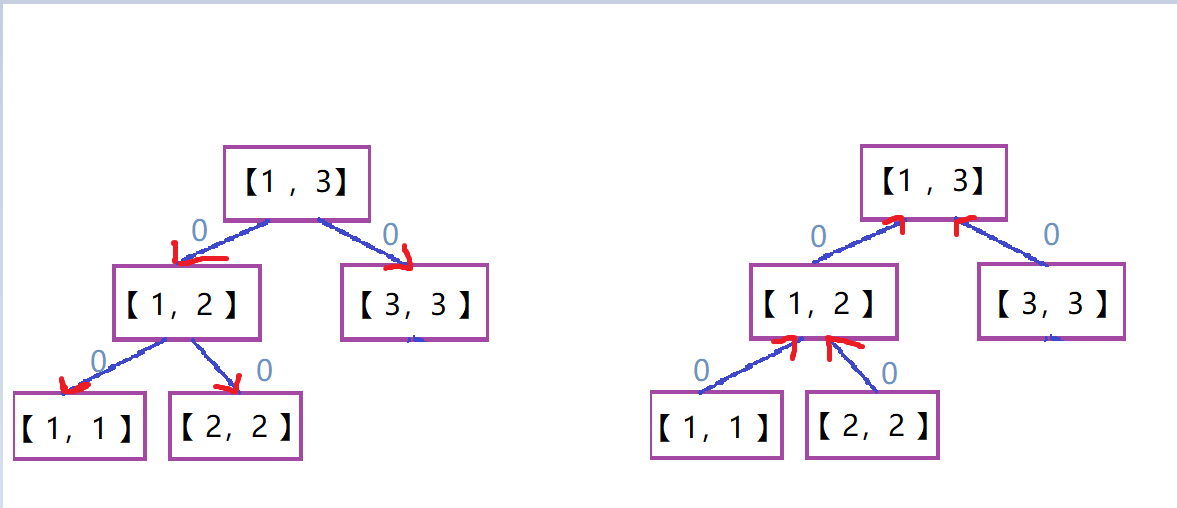
对于左边这个父亲指向儿子的线段树，叫它出树，对于右边这个儿子指向父亲的树，叫它入树
默认的，两边的对应的叶子节点应该用权值为\(0\)的无向边连接（接下来就不画了
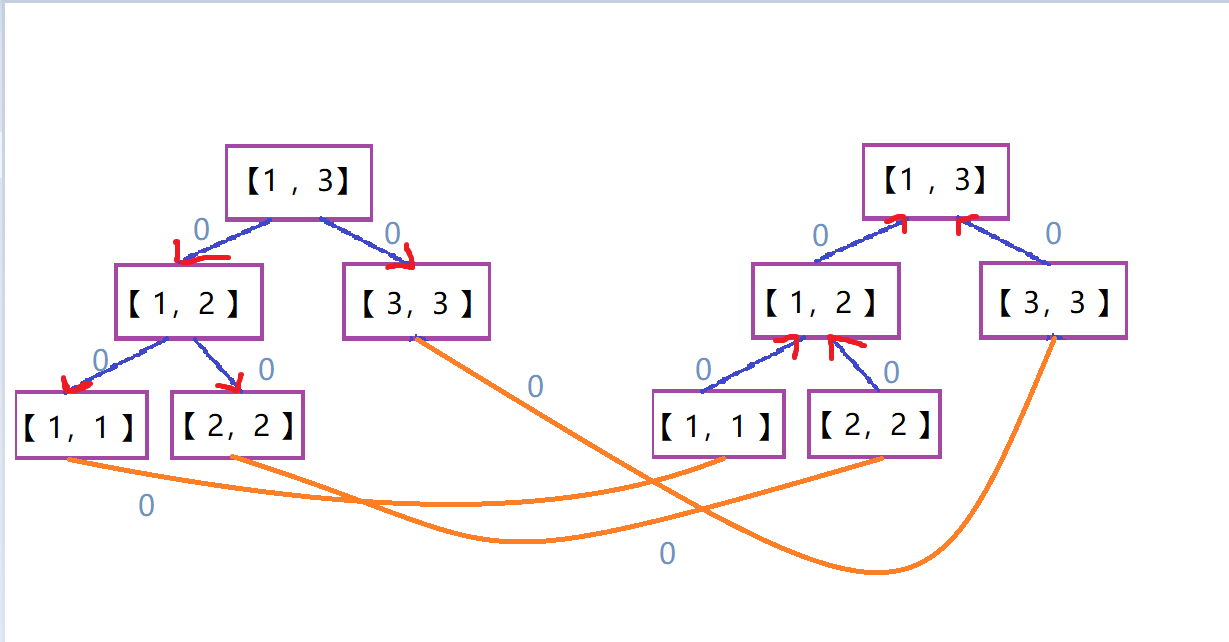
单点向区间
接下来，加上这条单点向区间的边，图是这样的：
因为都是叶子节点所以不明显（所以题目给的什么鬼样例啊）
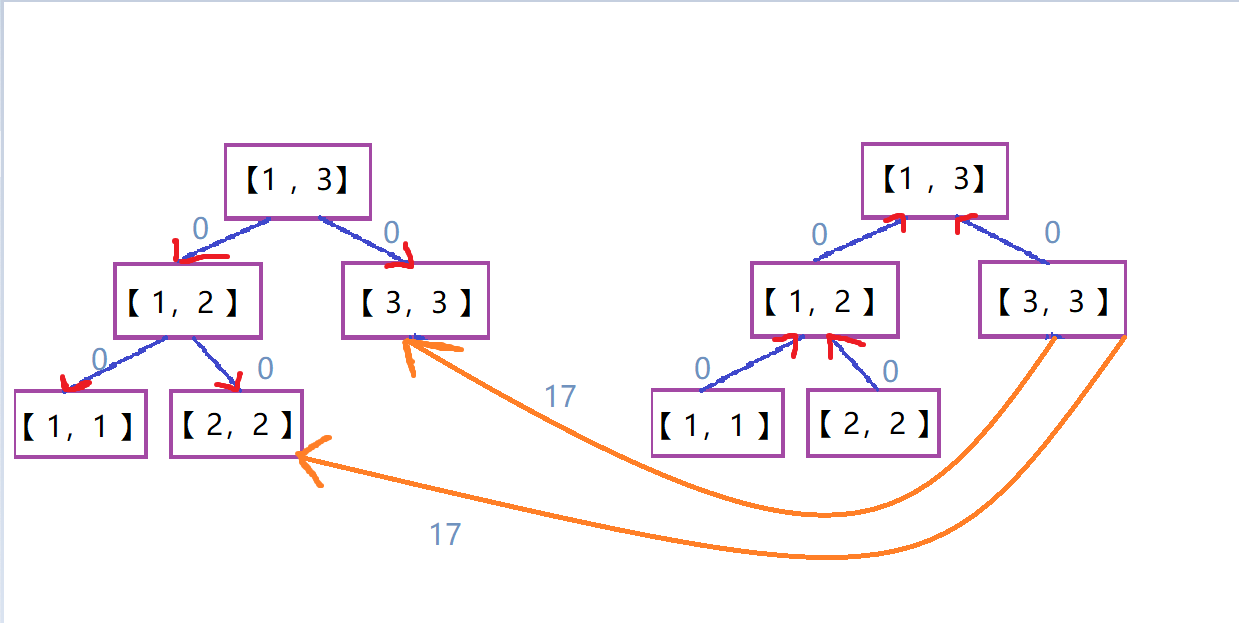
假设再建一个单点1向区间[1,3]连边，权值为10.
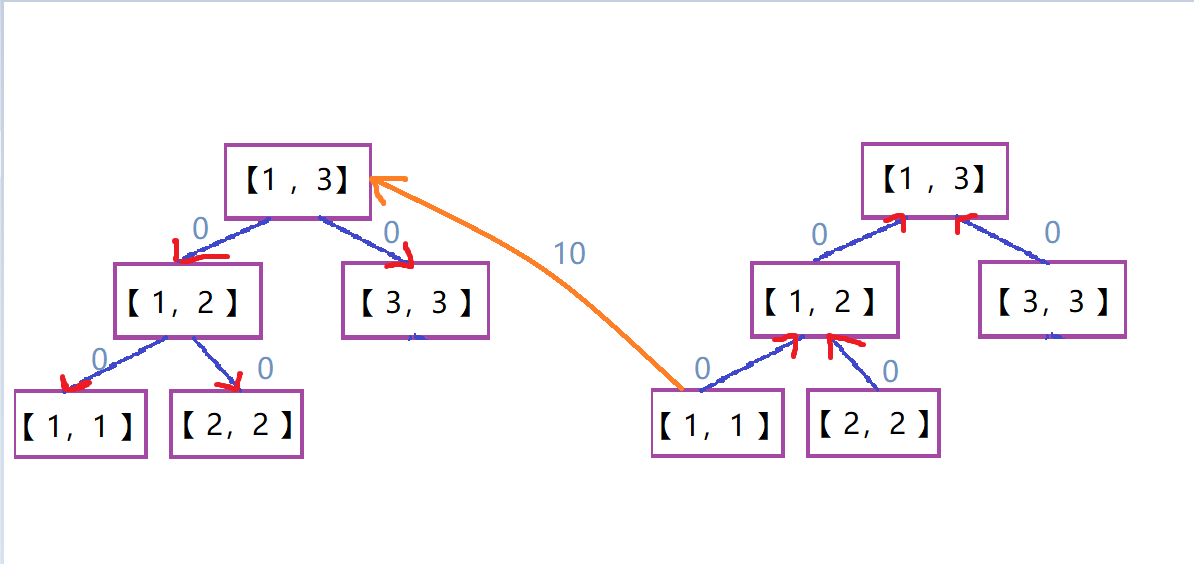
如果要跑这样一条路：\(1——>2\)
那么就是这样跑的：
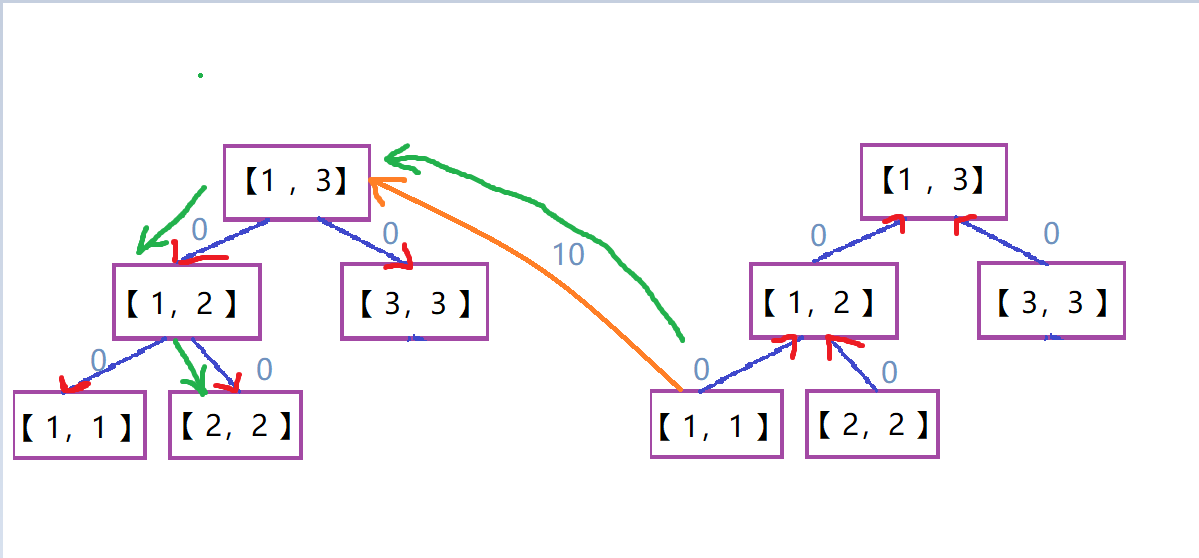
因为树内部是\(0\)所以最终的路径长还是10.
区间向单点
同理，如果是区间向单点连边。反过来搞就行了
假设\([1,3]\)向\(3\)连边。并要跑这样一条路：$ 1——>3 $,如下图
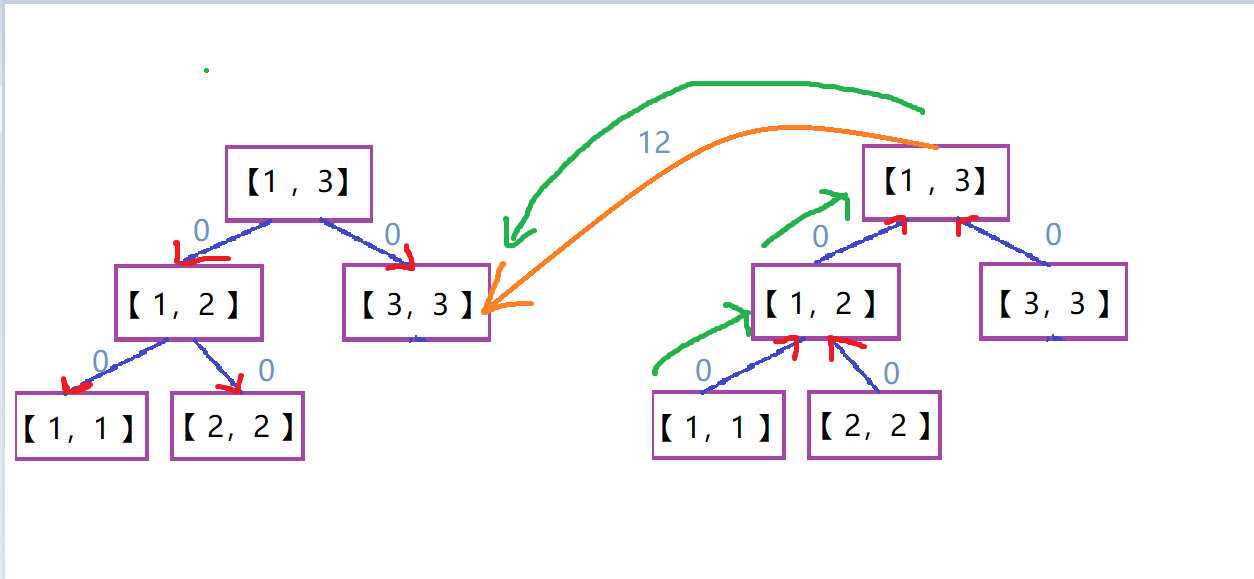
\(code\)
#include<bits/stdc++.h>
#define int long long
#define mid ((l+r)>>1)
using namespace std;
const int N=5e5+105;
const int INF=0x3f3f3f3f3f3f3f3f;
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*f;
}
int n,m,s,d[N],ls[N<<1],rs[N<<1];
int nex[N<<2],to[N<<2],v[N<<2],h[N<<2],cnt,tot;
bool vis[N<<2];
struct qwq{
int dis,id;
bool operator < (const qwq &x) const
{return x.dis<dis;}
};
priority_queue<qwq> q;
inline void pre(){
memset(d,0x3f,sizeof(d));d[s]=0;
}
inline void dij(int s){
q.push((qwq){0,s});
while(!q.empty()){
qwq tem=q.top();int x=tem.id;q.pop();
if(!vis[x]){
vis[x]=1;
for(int i=h[x];i;i=nex[i])
if(d[to[i]]>d[x]+v[i]){
d[to[i]]=d[x]+v[i];
if(!v[to[i]])q.push((qwq){d[to[i]],to[i]});
}
}
}
}
inline void add(int x,int y,int z){
to[++cnt]=y;v[cnt]=z;
nex[cnt]=h[x];h[x]=cnt;
}
void build1(int &p,int l,int r){//2操作
if(l==r){p=l;return ;}
p=++tot;
build1(ls[p],l,mid);build1(rs[p],mid+1,r);
add(p,ls[p],0);add(p,rs[p],0);
}
void build2(int &p,int l,int r){//3操作
if(l==r){p=l;return ;}
p=++tot;
build2(ls[p],l,mid);build2(rs[p],mid+1,r);
add(ls[p],p,0);add(rs[p],p,0);
}
int L,R;
void A(int p,int l,int r,int u,int w,int f){
if(L<=l && r<=R){
if(f)add(u,p,w);else add(p,u,w);
return ;
}
if(L<=mid)A(ls[p],l,mid,u,w,f);
if(mid<R)A(rs[p],mid+1,r,u,w,f);
}
signed main(){
n=read();m=read();s=read();
int rt1=0,rt2=0;tot=n;
build1(rt1,1,n);build2(rt2,1,n);
while(m--){
int opt,x,y,z;
opt=read();
if(opt==1){
x=read();y=read();z=read();
add(x,y,z);
}
else {
x=read();L=read();R=read();z=read();
if(opt==2) A(rt1,1,n,x,z,1);
else A(rt2,1,n,x,z,0);
}
}
pre();dij(s);
for(int i=1;i<=n;i++)printf("%lld ",(d[i]<INF?d[i]:-1));
return 0;
}
那如果是区间到区间怎么搞？
区间向区间
题意：
有\(n\)个点和许多双向边，点y用\(1~n\)编号。
用\(( a , b ),( c , d )\) 表示，对于任意两个点\(x\)，\(y\)，\(（a≤x≤b），（c≤y≤d）\) ,之间有一条边，权值为\(1\).
从\(P\)点出发，求到任意一个国家的最短路。
解题
其实很简单，只要树的区间连树的区间就行了。（之前不是叶子节点连区间嘛）
这个题因为是双向边，所以是双向的快乐要搞两遍。
又因为是权值都是\(1\),就更好搞了（指最短路）
\(code\):
//题目：T3 Path
//重构次数：3
//不压行
#include<bits/stdc++.h>
#define mid ((l+r)>>1)
using namespace std;
const int N=4e6+105;
int n,m,s,h[N<<1],cnt,tot,d[N],ls[N],rs[N],a,b,c,D,x,y;
int nex[N<<1],to[N<<1],val[N<<1];
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*f;
}
void add(int x,int y,int z){
to[++cnt]=y;val[cnt]=z;
nex[cnt]=h[x];h[x]=cnt;
}
void build(int &x,int &y,int l,int r){
if(l==r){x=l;y=l;return ;}
if(!x)x=++tot;if(!y)y=++tot;
build(ls[x],ls[y],l,mid);
add(ls[x],x,0),add(y,ls[y],0);
build(rs[x],rs[y],mid+1,r);
add(rs[x],x,0),add(y,rs[y],0);
}//递归建初始树
void A(int p,int l,int r,int x,int y,int z,int f){
if(x<=l &&y>=r){
if(f)add(z,p,0);else add(p,z,0);
return ;
}
if(x<=mid)A(ls[p],l,mid,x,y,z,f);
if(mid<y)A(rs[p],mid+1,r,x,y,z,f);
}
void dij(){
memset(d,0x3f,sizeof(d));
deque<int> q;d[s]=0;q.push_back(s);
while(!q.empty()){
int u=q.front();q.pop_front();
for(int i=h[u];i;i=nex[i])
if(d[to[i]]>d[u]+val[i]){
d[to[i]]=d[u]+val[i];
if(val[i])q.push_back(to[i]);else q.push_front(to[i]);
}
}
}
int main(){
n=read();m=read();s=read();
int rt1=0,rt2=0;tot=n;
build(rt1,rt2,1,n);
while(m--){
a=read();b=read();c=read();D=read();
x=++tot,y=++tot;
add(x,y,1);A(rt1,1,n,a,b,x,0);A(rt2,1,n,c,D,y,1);
x=++tot,y=++tot;
add(x,y,1);A(rt1,1,n,c,D,x,0);A(rt2,1,n,a,b,y,1);
}
dij();
for(int i=1;i<=n;i++)printf("%d\n",d[i]);
return 0;
}
朋友们，我出息了！呜呜呜……
书写ing
