精神网络学习笔记

本篇接上篇 深度学习笔记 喵~

1. 精神网络模型

考虑到在之前的模型中，我们训练的模型的决策界限都可以轻易找到其表达式，相对来说较为简单，我们下面来看一个复杂的模型，精神网络。

精神网络模型是通过模仿人的神经元的出的模型，即大脑中一般会分为多层神经元，第一层神经元负责接受一个输入，然后刺激第二层神经元，第二层神经元再刺激第三层神经元，最终将信息传输到大脑里。并且相邻两层在刺激的时候会对信号进行加工，以至于最终可以识别出信息。

我们之前讲的各种回归可以看作为一个两层神经元的配合，即通过输入一个向量 \(\mathbf{x}\)，将向量的第 \(i\) 个分量 \(x_i\) 的值作为第一层输入层神经元的输入，然后第二层神经元的输入是第一层神经元的输入通过一个函数 \(h_{\mathbf{\theta}}(\mathbf{x})\) 计算得出（即第二层的输入是第一层的输出）。最终第二层精神元的输入即视作分类结果（即该数据被分到正类的概率）。

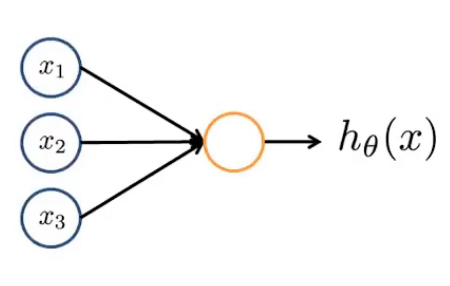
我们可以考虑更加复杂的情况，即在输入层和输出层之间多加几层神经元，我们称为隐藏层，然后这些隐藏层的输入也为上一层的输出。

即如果我们设 \(\mathbf{a}^{(i)}\) 为第 \(i\) 层精神元的输入，那么我们就可以对于每一层建立都建立一个函数模型：

\[\mathbf{a}^{(i + 1)} = h_{\mathbf{\Theta}^{(i)}}(\mathbf{a}^{(i)}) = g((\Theta^{(i)})^{\mathbf{T}} \mathbf{x}) \]

如果 \(\mathbf{x}\) 为一个 \(m\) 维向量，则我们约定记号 \(g(\mathbf{x})\) 代表 \(g(\mathbf{x}) = [g(x_1), g(x_2), \cdots, g(x_m)]^{\mathbf{T}}\)。我们将 \(g(x)\) 称为激活函数，一般我们会使用非线性函数来作为激活函数。

同样，我们在输入层和隐藏层中，每层加一个偏置量，即为图中的 \(a_0^{(i)}\)，和之前的两个回归的做法相似，我们让这个偏置量等于 1，所有的 \(a_0^{(i)} = 1\).

下图即为我们精神网络模型，我们将第 \(i\) 层非偏置结点的数量记作 \(s_i\)，精神网络的层数记为 \(L\).

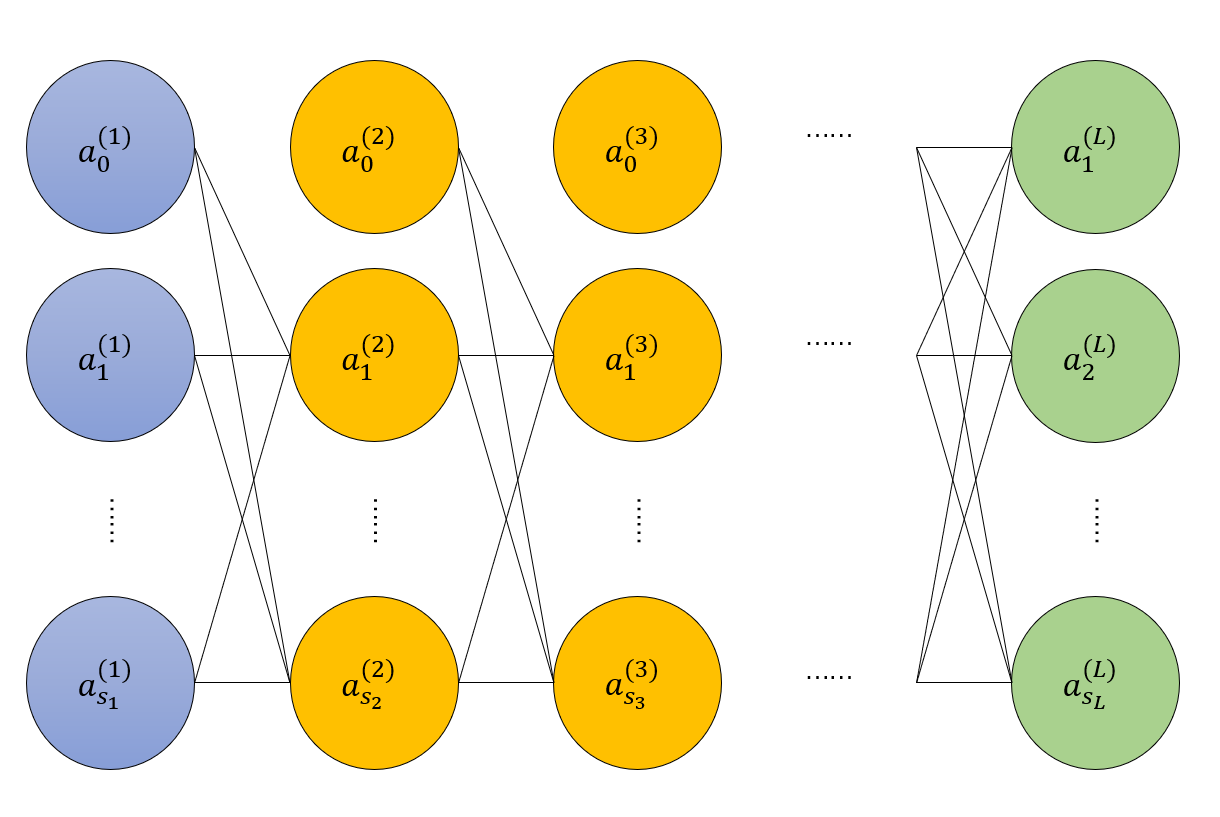
综上所述，对于第 \(k + 1\) 层的输入向量的第 \(j\,(j > 0)\) 个分量 \(a_j^{(k + 1)}\)，它和第 \(k\) 层的关系为：

\[a_j^{(k + 1)} = g\bigg(\sum_{i = 0}^{s_k} \theta_{ij}^{(k)} a_i^{(k)}\bigg) \]

我们不妨设 \(z_j^{(k + 1)} = \sum_{i = 0}^{s_k} \theta_{ij}^{(k)} a_i^{(k)}\)，此时我们将此式简化为 \(a_j^{(k + 1)} = g(z_j^{(k + 1)})\)。

2. 反向传播算法

我们还是希望通过梯度下降算法来训练精神网络模型。故接下来我们就要定义该模型代价函数了。我们可以像线性回归那样，将代价函数简单的定义为：

\[J(\Theta) = \frac{1}{2m} \bigg[ \sum_{i = 1}^m \sum_{j = 1}^{s_L} (a_j^{(L, i)} - y_j^{(i)})^2 + \lambda\sum_{k = 1}^{L - 1} \sum_{i = 1}^{s_k} \sum_{j = 1}^{s_{k + 1}}(\theta_{ij}^{(k)})^2 \bigg] \]

其中 \(a_j^{(L, i)}\) 为将训练集中第 \(i\) 组数据作为精神网络的输入，得到的输出向量中，第 \(j\) 个分量的值。如果我们将精神网络看作关于矩阵序列 \(\Theta\) 的一个函数模型，那么其实 \(a_j^{(L, i)} = \mathbf{h}_{\Theta}(\mathbf{x}_i)_j\).

不难发现尽管后面的那个三重和式求偏导非常容易，但是前面 \(a_j^{(L, i)}\) 是一个复合函数，对其求偏导非常麻烦，即难点主要集中在 \(\sum_{j = 1}^{s_L} (a_j^{(L, i)} - y_j^{(i)})^2\)。由链式法则的启发，我们就考虑相邻两层之间的偏导如何表示。

我们就仅考虑一组数据如何求 \(J(\Theta) = \frac{1}{2}\sum_{j = 1}^{s_L} (a_j^{(L)} - y_j)^2\) 的梯度，而之后对于多组数据，就对于各组数据分别求梯度然后相加即可。显然对于 \(\frac{\partial J}{\partial \theta_{ij}^{(k)}}\) 来说，根据求导的链式法则，我们有如下递推关系：

\[\frac{\partial J}{\partial \theta_{ij}^{(k)}} = \dfrac{\partial z_j^{(k + 1)}}{\partial \theta_{ij}^{(k)}} \dfrac{\partial a_j^{(k + 1)}}{\partial z_j^{(k + 1)}} \dfrac{\partial J}{\partial a_j^{(k + 1)}} \\ \frac{\partial J}{\partial a_i^{(k)}} = \sum_{j = 1}^{s_{k + 1}} \dfrac{\partial z_j^{(k + 1)}}{\partial a_i^{(k)}} \dfrac{\partial a_j^{(k + 1)}}{\partial z_j^{(k + 1)}} \dfrac{\partial J}{\partial a_j^{(k + 1)}} \]

递推边界为 \(\frac{\partial J}{\partial a_i^{(L)}} = a_i^{(L)} - y_i\).

而显然 \(\dfrac{\partial a_j^{(k + 1)}}{\partial z_j^{(k + 1)}} = g'(z_j^{(k + 1)}), \dfrac{\partial z_j^{(k + 1)}}{\partial \theta_{ij}^{(k)}} = a_i^{(k)}, \dfrac{\partial z_j^{(k + 1)}}{\partial a_i^{(k)}} = \theta_{ij}^{(k)}\)，故有：

\[\frac{\partial J}{\partial \theta_{ij}^{(k)}} = a_i^{(k)} g'(z_j^{(k + 1)}) \dfrac{\partial J}{\partial a_j^{(k + 1)}} \\ \frac{\partial J}{\partial a_i^{(k)}} = \sum_{j = 1}^{s_{k + 1}} \theta_{ij}^{(k)} g'(z_j^{(k + 1)}) \dfrac{\partial J}{\partial a_j^{(k + 1)}} \]

这样我们就可以通过先将数据作为输出，逐层计算其输出，然后从最后一层从后往前递推，求出所有的 \(\frac{\partial J}{\partial \theta_{ij}^{(k)}}\)，进而得到 \(\nabla J\)，然后就可以梯度下降了。

3. 初值设置

对于 \(\Theta\) 矩阵序列中各个元素的初值，我们最好不要将他们全部赋值为 0. 这是因为这会使得我们在计算梯度时，对于任意的 \(a, b\) 都有 \(\frac{\partial J}{\partial \theta_{ia}^{(k)}} = \frac{\partial J}{\partial \theta_{ib}^{(k)}}\)，进而最终的精神网络满足这样的性质 \(\theta_{ia}^{(k)} = \theta_{ib}^{(k)}\). 显然这样的精神网络会较为简单，可能会出现欠拟合的情况。

所以通常的做法是，初始将所有的 \(\theta_{ij}^{(k)}\) 赋值为在 \([-\epsilon, \epsilon]\) 的随机数。