Afternoon Tea - 形式语言与自动机

数学证明是一首叙事诗。

—— 知乎用户 “cyb 酱” 曾使用的签名

这里是 Nickel 自学离散数学中“形式语言与自动机”的相关内容时的笔记。由于是单纯的看书自学，就拉来了 Windy 一起学习，以减弱 消除 笔记的正式性，可以看做是一个随笔，这也意味这学校开设这门课程时会再有一个正式的笔记。其实发现这样的对话形式不容易排版，所以可能会很影响阅读体验（尤其是对于一些比较长的定义和证明）。

这里是基于上海科学技术文献出版社出版的《离散数学》来学习相关知识点的，如果之后看情况可能会揉进一些《算法导论》中的相关内容。根据书上内容，本篇只会介绍最简单的形式语言——正则语言以及有限自动机。

由于 \(\LaTeX\) 公式中似乎没有数学书上幂集符号所对应的公式，故使用 \mathcal{P}，即 \(\mathcal{P}\) 代替。博客园似乎不支持大写的带注释的箭头，即 \xRightarrow{}，故使用 \overset{}{\Rightarrow} 代替。

\[\newcommand{\lvert}{\left\vert} \newcommand{\rvert}{\right\vert} \newcommand{\cP}{\mathcal{P}} \newcommand{\bN}{\mathbf{N}} \newcommand{\Emp}{\mathsf{\Phi}} \newcommand{\emp}{\varnothing} \rule{750px}{1px} \]

Part 1 串和语言

W：好久没和 Nickel 一起学习了，让我们来看 Nickel 一直想学的内容吧，（翻书）第一节是“串和语言”看来书上想让我们从语言的定义本身学起。

N：看来是的，我曾看过《算法导论》中关于语言的相关内容，而书上似乎并没有很快给出语言的定义，它先告诉我们任意语言都是使用一些字符拼成的单词和句子相连接组成的。然后它将“单词”，“句子”抽象成字符串，并定义任意个符号组成的集合为字母表，其中的元素称为字母。通常我们使用小写字母表示字母，使用大写字母表示字母表。

W：这里还强调我们只讨论为有限集的字母表。接下来是串的严格定义：由字母表 \(V\) 中有限个字母组成的序列，并将串 \(w\) 中所含字符的个数称为串的长度，记作 \(\lvert w \rvert\)，规定空串记作 \(\lambda\)，其长度为 0。

N：感觉我们说话的语气好像自己没有学过字符串似的，不过下面就似乎很有趣了，为了表示所有长度为 \(k\) 的串组成的集合，我们可以将这些串看成一个个 \(k\) 元组，这很容易使我们想起笛卡儿积，所以我们用 \(V^k\) 就可以表示所有长度为 \(k\) 的串组成的集合了！

W：看来 Nickel 几个月来将这章前所有知识都过了一遍还是有一定好处的。可惜的是这样无法定义由空串组成的集合，所以要单独规定 \(V^0\) 为只有空串的集合，也可记作 \(\Lambda\)。有了这些就可以再形式化的定义 \(V^+\) 为所有非空串组成的集合，\(V^*\) 为所有串组成的集合。当然上述讨论的所有串都是 \(V\) 上的串。

N：和《算法导论》中似乎对上了，不过《算法导论》中似乎是用 \(\Sigma\) 表示的字母表。我们可以看到 \(V^+, V^*\) 都是可数集。当然了，有集合，那么怎么能少了运算呢？我们定义在 \(V^*\) 上的二元运算连接 \(\circ\) 如下：两个串 \(w = u_1 u_2 \cdots u_m, \varphi = v_1 v_2 \cdots v_n\) 的连接 \(w \circ \varphi\) 也是一个串，为 \(u_1 u_2 \cdots u_m v_1 v_2 \cdots v_n\)。我们将其简记为 \(w \varphi\)，而 \(w, \varphi\) 分别称为 \(w \varphi\) 的前缀和后缀，当 \(w \ne \lambda\) 时，则其可称为 \(w \varphi\) 的真前缀，同样当 \(\varphi \ne \lambda\) 时，\(\varphi\) 可称为 \(w \varphi\) 的真后缀。居然可以这样定义前缀后缀，感觉真是奇特。

W：当然我们只要能注意到 \(\lambda\) 为代数系统 \(\langle V^*, \circ \rangle\) 上的幺元，就不难发现该代数系统为一个独异点，并且其不可交换。连接运算的性质也很好注意到：\(\lvert w \varphi \rvert = \lvert w \rvert + \lvert \varphi \rvert\)。

N：当然由于 \(w\) 是可结合的，所以我们定义 \(w^k\) 为 \(\overset{k}{\overbrace{w \circ w \circ \cdots \circ w}}\)，即 \(w\) 的 \(k\) 次重复连接。当然我们再定义一种运算，求逆运算。称一个串 \(w = u_1 u_2 \cdots u_m\) 的逆为 \(w' = u_m u_{m - 1} \cdots u_1\)。显然此运算有以下性质：

\[\lambda = \lambda' \\ (w')' = w \\ w = \varphi \psi \Leftrightarrow w' = \psi' \varphi' \]

当一个串满足 \(w = w'\) 时，称为回文。当我看到书上使用 \('\) 表示串的逆时，我是拒绝的。

W：看来 Nickel 对不能随便使用加 ' 的变量这件事很敏感呢。不过有了这些知识，我们终于可以定义语言了，我们定义有限字母表 \(V\) 所生成的集合 \(V^*\) 的任意一个子集为 \(V\) 上的一个语言。语言通常用 \(L\) 表示。而字母表 \(V\) 上所有语言组成的集合正好就是幂集 \(\cP(V^*)\)。由于 \(V^*\) 是可数个有限集的并，所以 \(V^*\) 为可数集。即 \(V^*\) 和自然数集 \(\bN\) 等势，所以我们有 \(K[\cP(V^*)] = \aleph\)，即 \(\cP(V^*)\) 为不可数集。而当 \(V = \emp\) 时，\(V\) 上仅有空语言 \(\Emp\) 一种语言。

N：而由于语言是集合，所以集合上的运算都可以作用在语言上。而语言是由串构成的，故串的连接运算也可定义在语言上，故定义语言 \(L_1, L_2\) 的连接运算为 \(L_1 \circ L_2 = \{w \varphi | w \in L_1 \and \varphi \in L_2 \}\)，我们将其简记为 \(L_1 L_2\)，而且由于串的连接是不可交换的，故语言的连接也不可交换。并且跟串一样，\(\langle \cP(V^*), \circ\rangle\) 是一个独异点。

W：那我们就来看一下这个代数系统的性质吧，设 \(A, B, C, D\) 是在 \(V\) 上的任意语言，则：

\[A \Lambda = \Lambda A = A \\ (A \subseteq B) \and (C \subseteq D) \Rightarrow AC \subseteq BD \\ A (B \cup C) = AB \cup AC \\ (B \cup C) A = BA \cup CA \\ A (B \cap C) \subseteq AB \cap AC \\ (B \cap C) A \subseteq BA \cap CA \]

N：最后两个式子似乎有些奇怪呢，让我想一想……

W：感觉可能是如果 \(w, \varphi \in A\) 且 \(w \in B - C, \varphi \in C - B\) 但却可以有 \(w \varphi, \varphi w \in AB \cap AC\) 所导致的呢……

N：好神奇，Windy 也进步不少呢。我们接着往下看吧，语言也有逆运算。语言 \(L\) 的逆 \(L'\) 为 \(\{\varphi' | \varphi \in L\}\)，若一个语言满足 \(L = L'\) 则称其为镜像语言，需要注意镜像语言中的串不一定都回文，其实只要保证语言中所有串的逆都在语言中就可以。

W：由于语言的连接运算是可结合的，故定义 \(L^k\) 为 $\overset{k}{\overbrace{L \circ L \circ \cdots \circ L}} $，即 \(L\) 的 \(k\) 次重复连接。并定义 \(L^0 = \Lambda\)。看来下面是重头戏了，要介绍语言的 Kleene 闭包 \(L^*\) 和 + 闭包 \(L^+\) 了！下面是它们的定义：

\[L^* = \bigcup_{k = 0}^{\infty} L^k = \Lambda \cup L \cup L^2 \cup \cdots \\ L^+ = \bigcup_{k = 1}^{\infty} L^k = L \cup L^2 \cup \cdots \]

显然有 \(L^* = L^+ \cup \Lambda\)。我们称一元运算符 \(*\) 为 Kleene star（Kleene 星号）。

N：虽然感觉比《算法导论》上讲的要慢，但是好像还是有点晕，我要思考一下……

W：闭包的性质好像有点多啊，不过好多都比较显然，唯一需要笔头写一写才能证出来的是 \((A^* B^*)^* = (A \cup B)^* = (A^* \cup B^*)^*\)，今天看来 Nickel 已经很累了呢，我们明天再继续吧。

N：谢谢 Windy，明天第二部分再会 qwq！

Part 2 形式文法

N：昨天我们读到了形式语言，今天我们就开始学习形式文法了！我们再次类比自然语言中的语法来理解形式文法。

W：我们可以发现自然语言中的句子都是由“主谓宾定状补”等句子成分组成，然而这些句子成分还可以划分成各个短语，短语还可以在往下划分成一个个单词。如果我们将一个句子像这样不断划分，最终得到一个个单词，我们就可以得到一棵树形结构。

N：我们通过观察自然语言可以发现，一个文法要由“单词”，“句子结构”和“句子结构的排列顺序”。刚才 Windy 所说的句子成分，短语都属于我这里所说的句子结构。而“句子结构的排列顺序”就是诸如句子中“谓语必须在主语后”、“形容词在被修饰的名词前、句子中出现的括号必须配对”等规定。但这里要注意，我们强调形式文法拥有构造合乎文法的句子的功能，并不只有在学习自然语言文法中所强调的限制句子格式的作用。

W：形式文法和自然语言语法本质一样，所要强调的却不同，我想这可能和我们在学习自然语言通常是先学会如何说出一个简单句子而再去细究其语法，而对于形式语言来说，我们则是通过形式文法来理解形式语言内在的性质。

N：这么说形式语言大多是没有意义的呢……形式文法应该是研究形式语言内在结构的利器吧……

W：让我们回到数学上吧，我们不妨将“单词”，“句子结构”和“句子结构的排列顺序”抽象成数学中的概念，即形式文法的三个主要部分：终结符集、非终结符集、生成式集。

• 终结符集中的字符称为终结符，即通过文法规则的构造最终可以出现在句子中的字符；
• 非终结符集中就相当于是一个个的“句子成分”的名称组成的集合；
• 生成式集即相当于“句子结构的排列顺序”的集合，也就是文法规则。

N：所以我们可以定义形式文法 \(G\) 是有序四元组 \(\langle V_N, V_T, P, \sigma \rangle\)，其中 \(V_N\) 为非终结符集，\(V_T\) 为终结符集，\(P\) 为生成式集，\(\sigma\) 为开始符。要求 \(V_N \cap V_T = \emp, \sigma \in V_N\)，\(P\) 中的每一个元素即为一种生成式，我们通常将一种生成式记作：\(\alpha \rightarrow \beta\)，其中 \(\alpha = \varphi A \psi, \beta = \varphi w \psi\)，\(\varphi, \psi, w\) 均为字母表 \(V_N \cup V_T\) 上的一个串，所以他们有可能是空串，而 \(A\) 为非终结符。不难看出，生成式可以理解为一种句子的递归生成形式。

W：在形式文法 \(G = \langle V_N, V_T, P, \sigma \rangle\) 上，我们定义 \((V_N \cup V_T)^*\) 上的符号串为句型。如果 \(\alpha \rightarrow \beta\) 是一个生成式，\(w = \varphi \alpha \psi, \widetilde{w} = \varphi \beta \psi\) 是句型，则称 \(\widetilde{w}\) 为 \(w\) 的直接派生，记作 \(w \Rightarrow \widetilde{w}\)。如果 \(w_1, w_2, \cdots, w_n\) 为一串句型，其中 \(w_1 \Rightarrow w_2 \Rightarrow \cdots \Rightarrow w_n\)，则称 \(w_n\) 可由 \(w_1\) 派生得到或称 \(w_n\) 为 \(w_1\) 的派生，记作 \(w_1 \overset{*}{\Rightarrow} w_n\)。而有了派生的概念，我们就可以让开始符由一些作用了，并且还可以让形式文法生成一个语言了：记形式文法 \(G\) 生成的语言为 \(L(G)\)，它是由 \(\sigma\) 派生得到的所有终结符串组成的集合，即：

\[L(G) = \{w | w \in V_T^*, \sigma \overset{*}{\Rightarrow} w\} \]

N：我们其实不难发现，一个文法所产生的语言，主要有生成式来决定。文法还有分类，可以分为 4 类：

（0 型）无限止文法，对其生成式没有要求，要强调的是其生成式 \(\varphi A \psi \rightarrow \varphi w \psi\) 中 \(w\) 可以为空串，这样的话可使 \(\lvert \alpha \rvert > \lvert \beta \rvert\) 成立。我们称这样的规则为缩减规则，只有 0 型文法能缩减。0 型文法生成的语言可称为 0 型语言。

（1 型）上下文有关文法，在其生成式 \(\varphi A \psi \rightarrow \varphi w \psi\) 中，要求 \(w \ne \lambda\)，即要求所有生成式都是非缩减的。因此在 1 型文法中，如果有

\[w_1 \Rightarrow w_2 \Rightarrow \cdots \Rightarrow w_n \]

将一个特例 \(\sigma \rightarrow \lambda\) 排除后，则必有

\[\lvert w_1 \rvert \le \lvert w_2 \rvert \le \cdots \le \lvert w_n \rvert \]

由 1 型文法生成的语言可称为 1 型语言。

（2 型）上下文无关文法，在其生成式 \(\varphi A \psi \rightarrow \varphi w \psi\) 中，要求 \(\varphi = \psi = \lambda, w \ne \lambda\)，即排除特例 \(\sigma \rightarrow \lambda\) 后，生成式形如 \(A \rightarrow w\,(w \ne \lambda).\) 由 2 型文法生成的语言可称为 2 型语言。

（3 型）正则文法，在其生成式 \(\varphi A \psi \rightarrow \varphi w \psi\) 中，要求 \(\varphi = \psi = \lambda, w \ne \lambda\) 且串 \(w\) 中至多有一个非终结符。3 型文法还可以再分出两类特殊的文法：将全部生成式均形如 \(A \rightarrow a B\) 或 \(A \rightarrow a\) 的文法称作右线性文法，将全部生成式均形如 \(A \rightarrow Ba\) 或 \(A \rightarrow a\) 的文法称作左线性文法，其中 \(A, B \in V_N, a \in V_T\)。我们同样将由正则文法生成的语言称为正则语言。

W：在了解上述分类后，很容易发现，3 型文法 \(\subsetneqq\) 2 型文法 \(\subsetneqq\) 1 型文法 \(\subsetneqq\) 0 型文法。再强调 Nickel 所说的一个特例：生成式 \(\sigma \rightarrow \lambda\) 可以包含在任意 0 型文法中，不受上述文法种类的限制。

N：我们可以通过建立以 \(\sigma\) 为树根的派生树生成形式语言的一个句子，这正如前文自然语言中的树形结构一样，所以就不再赘述了……

W：感觉今天的知识可以让我们更好理解正则表达式了呢，到时候学会它就可以用它来快速匹配字符串了呢……

N：同样很期待，但是明天终于就要正式进入自动机相关内容了，让我们先把这个有意思的知识点学完吧！

Part 3 有限状态自动机

N：在学习完使用文法表示语言后，我们就可以学习有限状态自动机了，可以继续考虑类比现实中的一台信号转化器，其可以在任意时刻工作，为了方便，不妨设工作时间点 \(T = 0, 1, 2, \cdots\)。在 \(t = 0\) 时，我们对其进行一些设置并让其开始工作。之后在每一个时刻 \(t\)，机器都会收到一个输入信号 \(s(t)\)，并通过计算产生一个输出信号 \(r(t)\)。我们将提供给机器的一串输入信号 \(s(1)s(2) \cdots s(t)\) 称为一个激励，将所产生的输出信号称为机器 \(M\) 对此激励的响应。

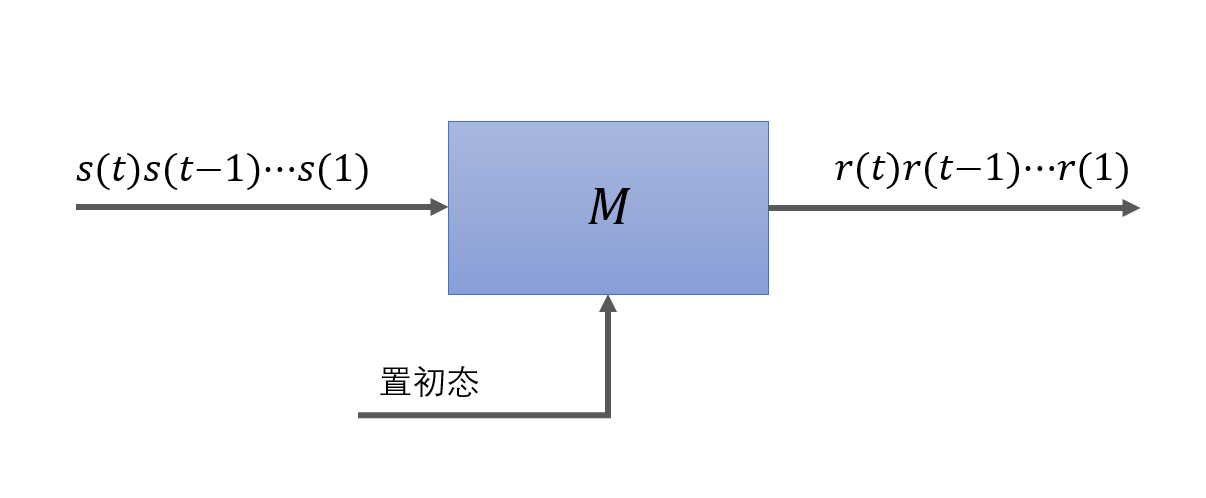
W：我们将所有输入符号组成的集合称为输入符号集 \(S\)，将输出符号组成的集合称为输入符号集 \(R\)。现实中的机器可以认为由有限个部件组成，而每一个部件都有有限种状态。不妨假设机器 \(M\) 由 \(N\) 个部件组成，并且用 \(q^{(i)}(t)\) 表示 \(t\) 时刻第 \(i\) 个零件的状态，则 \(t\) 时刻整个机器的状态 \(q(t)\) 可以使用一个 \(N\) 元组 \(\langle q^{(1)}(t), q^{(2)}(t), \cdots, q^{(N)}(t) \rangle\) 表示，由机器的所有不同状态组成的集合称为状态集 \(Q\)，状态集的大小即为机器各个零件状态数之积，机器在 \(t = 0\) 时的状态称为初始状态，记作 \(q_I\)，即 \(q_I = q(0).\)

N：机器 \(M\) 在接收到输入信号 \(s(t)\) 时，其机器状态的变化和对应输出信号 \(r(t)\) 需要由上一时刻机器的状态和输入信号共同决定，故我们将这样的对应关系分别用函数 \(f, g\) 表示，即 \(q(t) = f(q(t - 1), s(t)), r(t) = g(q(t - 1), s(t))\)。如果确定了上一时刻机器的状态和输入信号，就可以确定相应的输出，我们称这种机器为确定型的机器。

W：有限状态自动机顾名思义就是状态数是有限的机器。有了前文所述的概念，我们可以定义一种有限状态自动机，即转换赋值有限状态自动机 \(M\) 为一个六元组 \(\langle Q, S, R, f, g, q_I \rangle\)，各个字母的意义刚才我们已经提到了，这个机器种类型的机器称米兰机。由于它的输出字符不仅和输入的字符有关系，还和机器从哪一个状态转移过来有关。故也称为转换赋值机。

N：一个有限状态自动机可以使用状态表和状态图来描述。状态表中横着的表头是所有输入字符，竖着的表头是所有状态，表中每个格是对应输入和状态的下一个状态与输出字符。而状态图则是一个有向图，每一个结点表示一个状态，每一条有向边表示从一个状态到被指向状态的转换，有向边上的标记 \(s / r\) 表明了相应的输入符号和输出符号。对于初态 \(q_I\)，用一个指向它的箭头来标明。这幅图就是有限状态自动机的一部分。

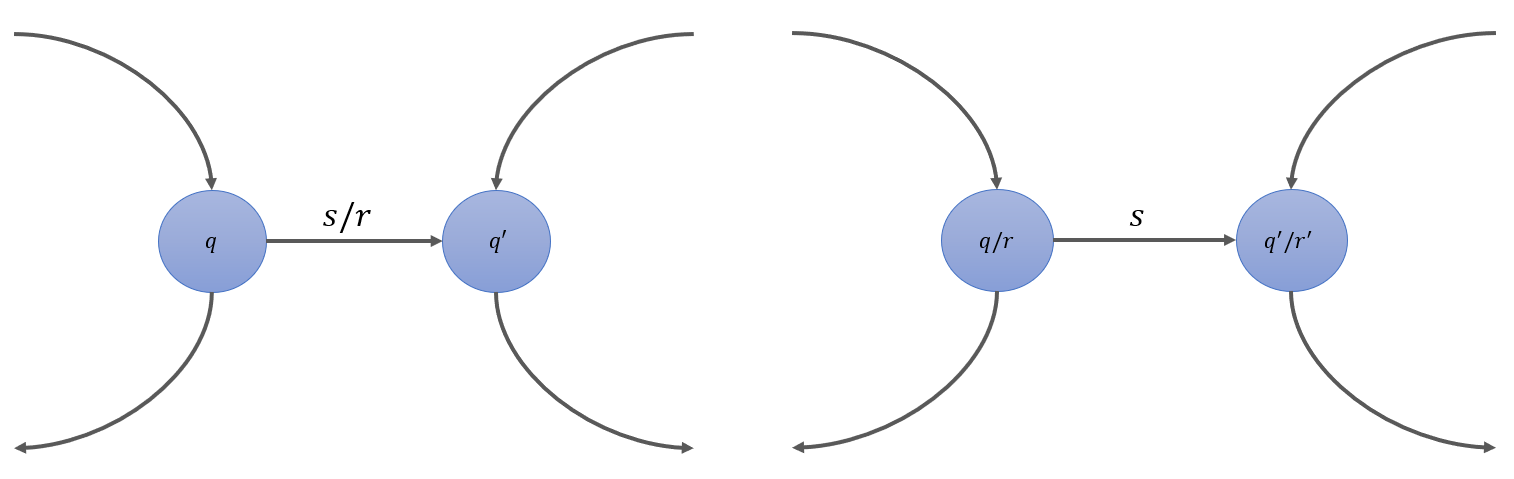
W：无论是图还是表，都可以表示函数 \(q' = f(q, s), r = g(q, s)\)，我们经常也将它们记为 \(q \xrightarrow{s/r} q'\)。我们经常将对激励 \(s(1)s(2) \cdots s(t)\) 所做出的响应 \(r(1)r(2) \cdots r(t)\) 和状态序列 \(q(0)q(1) \cdots q(t)\) 记为：

\[q(0) \xrightarrow{s(1)/r(1)} q(1) \xrightarrow{s(2)/r(2)} q(2) \xrightarrow{s(3)/r(3)} \cdots \xrightarrow{s(t)/r(t)} q(t) \]

N：还有一类有限状态自动机，其输出只和到达的状态有关，而从与哪个状态转换过来无关，这样的有限状态自动机，称为状态赋值机，又称摩尔机。在定义这类有限状态自动机时，我们只要将前面的定义精简一下，就可以了：将这个六元组用 \(M = \langle Q, S, R, f, h, q_I \rangle\) 表示，其和刚才提到的转换赋值机的区别在于将 \(g: Q \times S \rightarrow R\) 变为了 \(h : Q \rightarrow R\)，因为不需要考虑机器之前的状态了。所以状态表的格子中只会写对应的下一个状态，而在表的最右一列写上表各状态对应的输出，而状态图中的点标记为 \(q/r\) 表明状态和对应的输出，而边的标记则为 \(s\)，表明输入字符产生的状态转移。同样，状态转移可表示为 \(\langle q, r \rangle \xrightarrow{s} \langle q', r' \rangle\)。

Part 4 两类自动机的转换

N：我们已经学习了两类有限状态自动机，这两类有限状态自动机也可以相互转换，在这之前，让我们先来接受后继的概念……

W：说实话，感觉做了这么多图论题后，只要稍微想一想就可以知道这两种机器怎么转换。然而在看了书上的公式推导后，我反而感到很晕……

N：不过看一些定义还是有一点用处的。让我们回到正题，如果在有限状态机 \(M\) 中有 \(f(q, s) = q'\)，则称 \(q'\) 是状态 \(q\) 的 \(s\) -后继，记为 \(q \xrightarrow{s} q'\)，如果对于输入串 \(w = s(1)s(2) \cdots s(t)\) 将 \(M\) 从状态 \(q = q(0)\) 转向 \(q' = q(t)\) 即：

\[q = q(0) \xrightarrow{s(1)} q(1) \xrightarrow{s(2)} q(2) \xrightarrow{s(3)} \cdots \xrightarrow{s(t)} q(t) = q' \]

称状态 \(q'\) 为状态 \(q\) 的 \(w\) -后继，记作 \(q \overset{*}{\Rightarrow} q'\) 并称 \(q(0)q(1) \cdots q(t)\) 是 \(w\) 的可接受状态序列。

W：我们容易知道，对于两类自动机，我们可以将它们统一输出记作 \(r(t) = O(q_I, s(1)s(2) \cdots s(t)), \, (t \ge 1)\)。对于状态赋值机有 \(r(0) = h(q_I)\)，但转换赋值机却在初态没有输出。并且易知 \(f(q, w \varphi) = f(f(q, w), \varphi), O(q, w \varphi) = O(f(q, w), \varphi)\)。

N：有了这些性质，我们先给出两类机器相似的定义，我们考虑一个状态赋值机 \(M_s\) 和状态转换机 \(M_t\)，如果对于每一激励，\(M_s\) 的响应恰好等于 \(M_t\) 的响应前面加任一且确定的输出符号，称 \(M_s\) 和 \(M_t\) 是相似的。

W：我们现在说明如果我们有 \(M_s = \langle Q, S, R, f, h, q_I \rangle\)， 则必然可以构造出 \(M_t = \langle Q, S, R, f, g, q_I \rangle\)，与之相似，其实只需使得 \(g(q, s) = h(f(q, s)), q \in Q, s \in S\) 成立即可，如果从状态图上来看，就是将除初态外每一个状态的输出都重新填到所有指向该状态的边上即可。

N：如果反过来，已知一个 \(M_t\) 要构造出与之相似的 \(M_s\)，就稍微要想一下了，有一个问题是在 \(M_t\) 中从不同状态到达同一个状态的输出字符不同。于是我们考虑拆点，即若到达一个状态会产生 \(c\) 个输出，则就将其拆成 \(c\) 个状态，再让原先各个不同的边指向对应的状态，如果形式化的讲，即 \(M_t = \langle Q, S, R, f_t, g, q_I \rangle, M_s = \langle Q, S, R, f_s, h, \langle q_I, r_0 \rangle \rangle\)，即在构造出的 \(M_s\) 中，我们使用我们不再使用单个字符而是使用二元组 \(\langle q, r \rangle\) 给状态编号，代表在 \(M_t\) 中 \(q\) 这个状态被多个对应的输出拆成的相应状态，即若在 \(M_t\) 中有 \(q \xrightarrow{s / r} q'\) 那么，在 \(M_s\) 中有 \(\langle \langle q, r' \rangle, r' \rangle \xrightarrow{s} \langle \langle q', r \rangle, r \rangle\)。如果写成函数的形式，即为 \(\forall r \in R, f_s(\langle q, r' \rangle, r') = \langle q', r \rangle, h(\langle q', r \rangle) = r\)。显然我们可以任取 \(\langle q_I, r \rangle\) 中的任意一个 \(\langle q_I, r_0 \rangle\) 做初态，初态其实并不需要拆点，但是我们选择的 \(r_0\) 会成为激励为空串时 \(M_s\) 的响应。

W：感觉这一节知识容量有些小，不过下下节就可以将自动机和正则文法对应起来了，还是很期待的 ~

N：似乎 Windy 期待的有些早呢……

Part 5 有限自动机的简化

N：感觉和上次编辑有一段时间了……有些知识得复习一下……

W：上次说到的两类自动机的转化，其实当时学的时候就发现了如果将一个转换赋值机转化为状态赋值机，那么自动机的结点数量会增加，而转化前后自动机的功能没有改变，所以自动机是可以被简化的。

N：在研究简化方法前，我们需要想办法描述两个有限自动机功能相同。我们只需要求这两台自动机 \(M_1, M_2\) 的输入输出字符集相同，对于任意一个非空激励的输出相同即可，这时我们称两台自动机等价。

W：两台自动机等价的概念过于宏观，我们更善于把握微观的信息。我们不妨先定义状态等价，即对于自动机 \(M\) 的两个状态 \(q_a, q_b\) 来说，它们是等价的当且仅当将它们分别作为 \(M\) 的初态所生成的两个自动机等价，记作 \(q_a \sim q_b\)。

N：其实两个状态的等价定义就是从这两个状态开始如果输入一样，那么输出也一样。那么就可以得出对于两个等价状态的 \(w\) -后继，从它们开始接受相同激励 \(\varphi\) 的输出，可以看作是原先两个等价状态接受 \(w \varphi\) 输出的连续子串。所以两个等价状态的任意 \(w\) -后继也等价。

W：但是由于输入字符串集合是无限集，我们不能通过定义判断两个状态是否等价。所以我们找到一个更弱的定义：\(k\) -等价，即对于两个状态 \(q_a, q_b\) 来说，对于任意 \(\lvert w \rvert \le k\) 的激励，有 \(O(q_a, w) = O(q_b, w)\)，则称这两个状态 \(k\) -等价，记作 \(q_a \overset{k}{\sim} q_b\)。

N：上面两个等价关系都可以诱导出在状态集 \(Q\) 上的划分，即各个等价类。我们将 \(k\) -等价诱导出的划分记为 \(P_k = \{[\,q\,]_k | q \in Q \}\)，将等价诱导出的划分记为 \(P = \{[\,q\,] | q \in Q\}\)。由定义可知 \(q_a \sim q_b \Rightarrow q_a \overset{k + 1}{\sim} q_b \Rightarrow q_a \overset{k}{\sim} q_b\,(\forall k \in \textbf{N}^*)\)。

W：我们需要找到一个将 \(P\) 和 \(P_k\) 连接的桥梁，我们发现一个结论：

\(P = P_k\) 当且仅当 \(P_k = P_{k + 1}\)。

必要性比较显然，下面证其充分性：

使用反证法，设 \(P_k = P_{k + 1}\) 且 \(P \ne P_k\)，则必有存在两个状态 \(q_a, q_b \in Q, q_a \overset{k}{\sim} q_b, q_a \nsim q_b\)。则必然存在一个最小的 \(j\)，\(j > k\) 并且使得 \(q_a \overset{j}{\nsim} q_b\)。

当 \(j = k + 1\) 时，\(q_a \overset{k + 1}{\nsim} q_b\)，进而推出 \(P_k \ne P_{k + 1}\)，矛盾。

当 \(j > k + 1\) 时，则必然存在一个长度为 \(j\) 的字符串 \(w\)，使得 \(O(q_a, w) \ne O(q_b, w)\)。我们不妨将 \(w\) 分解为 \(w = \varphi \psi\)，其中 \(\lvert \varphi \rvert > 0\) 且 \(\lvert \psi \rvert = k + 1\)。若设 \(q_a' = f(q_a, \varphi), q_b' = f(q_b, \varphi)\)，则有 \(O(q_a', \psi) \ne O(q_b', \psi)\)，则 \(q_a' \overset{k + 1}{\nsim} q_b'\)。而对于任意长度不超过 \(k\) 的字符串 \(\mu\) 来说， \(\lvert \varphi \mu \rvert \le j - k - 1 + k = j - 1\)，由于 \(j\) 的最小性，所以有 \(q_a \overset{j - 1}{\sim} q_b\)，进而 \(O(f(q_a, \varphi), \mu) = O(f(q_b, \varphi), \mu)\)，即 \(O(q_a', \mu) = O(q_b', \mu)\)，则有 \(q_a' \overset{k}{\sim} q_b'\)，进而推出 \(P_k \ne P_{k + 1}\)，矛盾。

综上，故有 \(P = P_k\)。

N：我们也比较容易得知 \(q_a \overset{k + 1}{\sim} q_b\) 的充要条件为 \(q_a \overset{k}{\sim} q_b\) 且对于任意字符 \(s \in S\) 都有 \(f(q_a, s) \overset{k}{\sim} f(q_b, s)\)。

W：我们完善了找等价类的方法，那么如果要化简一台有限自动机 \(M\)，只需将各个状态都找到其所在的等价类，构造一个与 \(M\) 输入输出字符集相同的有限自动机 \(M'\)，而 \(M'\) 中的每一个状态对应 \(M\) 中的唯一的一个等价类，且 \(M'\) 中状态的连边和输出即对应 \(M\) 中相应等价类的状态间的连边与输出。这样就完成了自动机的简化。

N：感觉和缩点的思维很像呢……

W：当时看书上的描述时，我还没有反应过来。但这样熟悉的感觉，应该不会随着这个章节的完结而消散吧……

N：虽然感觉 Windy 有点语无伦次，但是马上就到最后一节了，加油！

Part 6 有限状态机与正则语言

N：距离上一次学习又过了一段时间呢，终于可以将有限状态机的学习告一段落了。

W：是的，我们今天要考察的，是有限状态机和正则语言的关系。我们考虑构造这样一种有限状态机 \(M\)，其可以识别某个串 \(w\) 是否在一个语言 \(L\) 中。形式化的来讲，自动机对于一个激励 \(w\)，如果 \(w \in L\)，则有 \(O(q_I, w) = 1\)，否则有 \(O(q_I, w) = 0\)。

N：而 \(O(q_I, w)\) 和 \(q_I\) 的 \(w\)-后继有关，故我们可以在状态集 \(Q\) 中构造一个子集 \(F\)，使得 \(f(q_I, w) \in F\) 当且仅当 \(O(q_I, w) = 1\)，我们将 \(F\) 称为终态集，将终态集中的状态称为终态，在状态机中用双圈表示。

W：然而对于判断一个串 \(w\) 是否在语言中，我们其实不用关心其作为激励在自动机中的输出，我们只需关心 \(f(q_I, w)\) 是否为终态即可。所以我们可以简化定义一个有限状态接受器是五元组 \(M = \langle Q, S, \delta, I, F \rangle\)，\(Q\) 为状态集，\(S\) 为输入字符集，\(I \subseteq Q\) 为初态集，\(F \subseteq Q\) 为终态集，\(\delta\) 为 \(Q \times S \rightarrow Q\) 的关系，称为 \(M\) 的转换关系，当 \(q' \in \delta(q, s)\) 时，就有 \(q \overset{s}{\rightarrow} q'\)。

N：对于一个有限状态接受器 \(M\)，若存在 \(q_I \in I\)，使得 \(\delta(q_I, w) \cap F \ne \emp\)，则称 \(w\) 被 \(M\) 接受。所有被 \(M\) 接受的输入字符串组成的集合为 \(M\) 可接受的语言，记为 \(L(M)\)。

W：值得注意的是，对于有限状态接受器，其可以有多个初态，并且我们注意关心对于激励的 \(w\)-后继是否在终态集当中，以此决定激励是否被接受。并且对于某个状态 \(q\) 的 \(s\)-后继，其不一定唯一，也不一定存在，即 \(\delta(q, s)\) 为一个状态集合而不是一个确定的状态。

N：不过当 \(\delta\) 为 \(Q \times S \rightarrow Q\) 的一个函数且 \(I\) 中仅有一个状态时，我们称 \(M\) 为确定的有限状态接受器，否则称其为不确定的有限状态接受器。对于一个不确定的有限状态接收器 \(M\)，都有一个确定的有限状态接受器 \(M'\)，使得 \(L(M) = L(M')\)。但是这个定理的证明好像在一个外国文献上……

W：那么我们先看一下有限状态接收机和 3 型文法的关系吧，设 \(G = \langle V_N, V_T, P, \sigma \rangle\) 为一个 3 型文法，则存在一台有限状态接受器 \(M = \langle Q, S, \delta, I, F \rangle\)，使得 \(L(M) = L(G)\)。书上又是各种符号化的证明……好难受啊……

N：那我们就考虑对于给定的 \(G\)，我们构造出一个 \(M\) 的方法，虽然这样可能并不严谨，但是我们可以更好的理解证明的过程。首先肯定有 \(V_T = S\)，其他的集合间关系不是很好表述，不过我们可以通过生成式集 \(P\) 作为突破口。对于 3 型文法来说，其生成式无非以下几种形式：（设 \(A, B \in V_N, a \in V_T\)）

\[A \rightarrow Ba, A \rightarrow aB, A \rightarrow a, \sigma \rightarrow \lambda \]

对于前两种，我们可以将其对应为 \(M\) 中 \(B \in \delta(A, a)\)，但似乎无法确定是前两种的哪一种，我们可以考虑对前两种生成式分开，分别构造自动机。而对于第三种，我们可以引入一个新状态 \(C \notin V_N\)，作为所有句子的结尾（终态），即 \(C \in \delta(A, a)\)，而对于第四种，我们可以让 \(\sigma \in F\) 来解决此问题。

这样我们就有 \(S = V_N \cup \{C\}, C \notin V_N\) 且 \(I = \{\sigma\}\)。当 \(P\) 中没有生成式 \(\sigma \rightarrow \lambda\) 时，\(F = \{C\}\)，否则 \(F = \{\sigma, C\}\)。

W：那我就来说如何根据一个 \(G\) 构造出一个 \(M\) 吧。我们先考虑当 \(I\) 只包含一个初态的时候，我们将初态 \(q_I\) 对应初始符 \(\sigma\)，状态集 \(Q\) 中所有状态和非终结符集 \(V_N\) 中的字符一一对应，\(P\) 的构造方式也跟 Nickel 所述相仿：若 \(\delta(A, a) = \{B_1, B_2, \cdots B_k\}\)，则 \(P\) 中就有生成式 \(A \rightarrow aB_1, A \rightarrow aB_2, \cdots, A \rightarrow aB_k\)，若 \(B_i \in \delta(A, a)\) 且 \(B_i \in F\)，则 \(P\) 中有生成式 \(B \rightarrow a\)。若 \(I \cap F \ne \emp\)，则 \(P\) 中有生成式 \(\sigma \rightarrow \lambda\)。

而当 \(I\) 有多个初态时，我们可以先将自动机外加一个状态 \(C\)，然后 \(C\) 向所有与初态集相连的状态连对应的边。然后再删去整个初态集内的状态，将 \(C\) 当作新的初态，这样就转化为了只包含一个初态的情况。

N：似乎就没有了呢，感觉这本教材并没有什么比较硬核的知识的样子，可能只是起到普及概念的作用……

W：回头如果有机会，还想和 Nickel 继续看其他的自动机相关知识，这次有点意犹未尽呢。

N：那么随缘了（x