算法漫游指北(第十四篇):二叉树的深度优先遍历、前序遍历(递归方式/非递归方式)、中序遍历(递归方式/非递归方式)、后序遍历(递归方式/非递归方式)
一、二叉树的深度优先遍历
递归实现先序、中序、后序非常强大的地方是每个都会访问同一个节点三次,所以三个遍历方式只是调换一下函数执行顺序。
无论是否是递归方式都用到了栈(函数栈也是栈):因为树的结构是从上到下访问,如果要返回去访问另一处的节点,那么必须要有栈来“记忆”。
前序遍历
在先序遍历中,我们先访问根节点,然后递归使用先序遍历访问左子树,再递归使用先序遍历访问右子树 根节点->左子树->右子树 Python代码实现:
递归方式前序遍历
def pre_order_traversal(self, node):
"""递归实现前序遍历"""
if node == None:
return
print(node.elem,end=' ')
self.pre_order_traversal(node.lchild)
self.pre_order_traversal(node.rchild)
思路:
1、先打印根节点
2、再执行self.pre_order_traversal(node.lchild)递归的寻找到二叉树的左节点,
此时左边的节点也作为一个树的根节点,打印,
直到找到树的左边的叶节点,
打印左边的叶节点,打印这个叶节点的所在树的右边的叶节点。
3、返回上一层树,已经处理完上一层树左边的子树,开始处理上一层树的右子树
也是先打印这个右子树的根节点,如果这个子树层次多,需要递归则重复第二步
4、处理完右子树继续返回上一层树,递归的处理完整个二叉树的左子树,开始处理右子树。
重复执行第二步,直到递归到最右的叶节点,叶节点的lchild或者rchild为None,则结束递归。
非递归方式前序遍历
def pre_order_traversal_not_recursion(self,node):
"""前序遍历,非递归方式"""
if node == None:
return
ret = []
stack = []
while node or stack:
while node:
ret.append(node.elem)
stack.append(node)
node = node.lchild
if stack:
t = stack.pop()
node = t.rchild
return ret
思路:
-
使用列表保存结果;
-
使用栈(列表实现)存储节点;
-
当根节点存在,保存结果,根节点入栈;
-
将根节点指向左子树;
-
根节点不存在,栈顶元素出栈,并将根节点指向栈顶元素的右子树;
-
重复步骤3-6,直到栈空。
中序遍历
在中序遍历中,我们递归使用中序遍历访问左子树,然后访问根节点,最后再递归使用中序遍历访问右子树 左子树->根节点->右子树 Python代码实现:
递归方式中序遍历
def in_order_traversal(self, node):
"""递归中序遍历"""
if node is None:
return
self.in_order_traversal(node.lchild)
print(node.elem, end=" ")
self.in_order_traversal(node.rchild)
思路:
1、先递归的执行寻找左节点,直到找到左子树的左边的叶节点,打印,
2、然后找到该层子树的根节点,右节点,返回上一层
3、已经处理完该层的左子树,打印该层的根节点,然后处理右子树,重复第二步
4、当整个二叉树做子树已经处理完后,打印根节点,处理右子树,重复第二步。
5、当处理到右子树最右的叶节点时,递归结束。
非递归方式中序遍历
def in_order_traversal_not_recursion(self,node):
"""非递归方式的中序遍历"""
if node == None:
return
ret = []
stack = []
while node or stack:
while node:
stack.append(node)
node = node.lchild
if stack:
t = stack.pop()
ret.append(t.elem)
node = t.rchild
return ret
思路:
-
使用一个栈保存节点(列表实现);
-
如果节点存在,入栈,然后将当前指针指向左子树,直到为空;
-
当前节点不存在,则出栈栈顶元素,取得当前节点的值,并把当前指针指向栈顶元素的右子树;
-
栈不为空,循环2、3步。
后序遍历
在后序遍历中,我们先递归使用后序遍历访问左子树和右子树,最后访问根节点 左子树->右子树->根节点 Python代码实现:
递归方式后序遍历
def post_order_traversal(self, node):
"""递归的后序遍历"""
if node is None:
return
self.post_order_traversal(node.lchild)
self.post_order_traversal(node.rchild)
print(node.elem, end=" ")
思路:
1、先递归的寻找左节点,直到左子树的最左边的叶节点,打印这个节点的值
2、返回上一层,递归的该子树找到右节点打印,返回上一层
3、重复执行第二步,直到处理完整个二叉树的左子树,开始处理右子树,重复第二步
4、直到整个二叉树的左右子树都处理完了,打印根节点的值,递归结束。
非递归方式后序遍历
def post_order_traversal_not_recursion(self, node):
"""非递归方式的后序遍历"""
if node == None:
return
ret = []
stack = []
while node or stack:
while node:
ret.append(node.elem)
stack.append(node)
node = node.rchild
if stack:
top = stack.pop()
node = top.lchild
return ret[::-1]
思路:
后续遍历根节点,先遍历左子树,然后遍历右子树,此时反过来考虑:先遍历根节点,然后遍历右子树,最后是左子树,这样就可以转化为和先序遍历一个类型了,最后只把遍历结果逆序输出就ok了,而先序遍历是之前写过并且比较好理解的。
-
使用栈存储节点;
-
当节点存在或者栈不为空,判断节点;
-
当节点存在,节点值保存,节点入栈,并将指针指向节点的右子树;
-
当栈不为空,节点出栈,并将指针指向左子树;
-
重复2-4直到结果产生;
-
逆序输出结果,利用Python列表的-1.
重建二叉树图
例如:已知前序遍历的结果为:ABDHIEJKCFLMGNO,中序遍历的结果为:HDIBJEKALFMCNGO。
思路: 1)、根据前序遍历结果确定根节点。 前序遍历的第一个节点为根节点。 2)、在中序遍历结果中找到根节点,根节点左侧的部分为左子树节点,根节点右侧的部分为右子树节点。 3)、将中序遍历的结果按根节点分为两部分,迭代的执行第一步和第二步,直到还原整个二叉树。
重画解答过程
1、前序遍历结果为ABDHIEJKCFLMGNO,则根节点是A,
根据中序遍历结果,将HDIBJEKALFMCNGO分为两个部分,HDIBJEK、LFMCNGO,即左子树和右子树
2、左子树HDIBJEK,根据前序遍历结果第二个,B是这个子树的根节点,
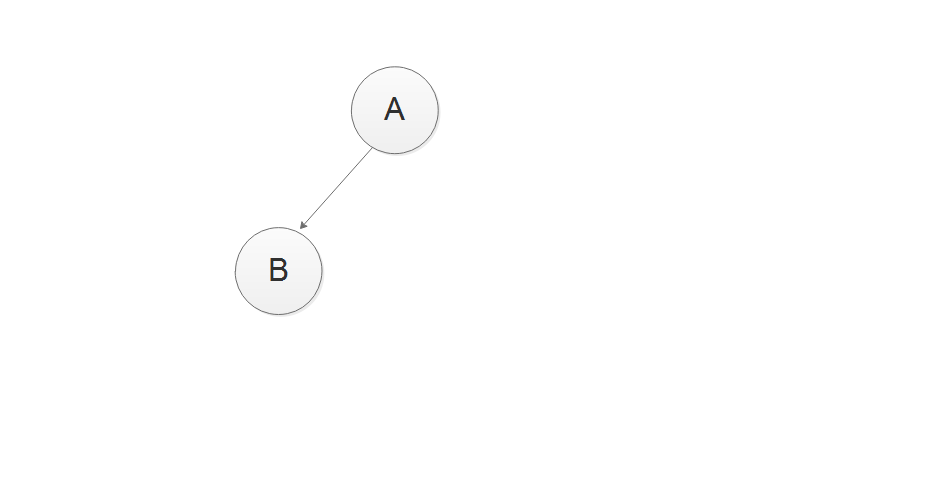
根据中序遍历结果,再次将这个子树分割成2个部分,HDI和JEK,
3、根据前序遍历结果,D为HDI这个子树的根节点,
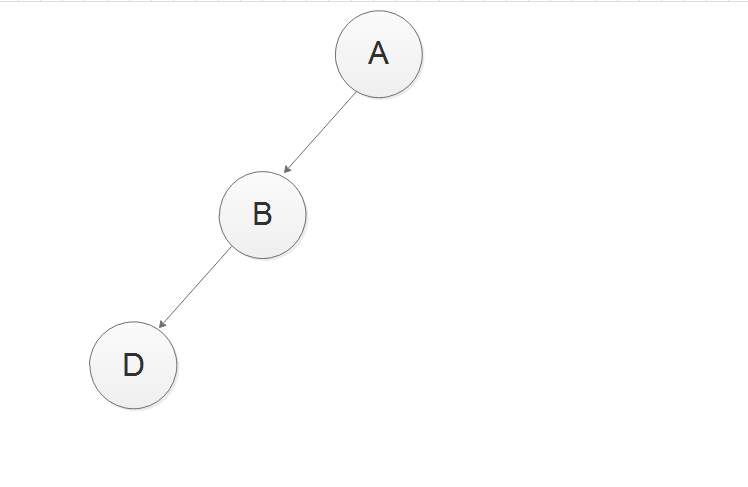
针对HDI这个左子树,因为中序遍历规则是左节点--根节点--右节点,根据中序遍历结果,H为这个子树的左节点,I为这个子树的右节点。所以添加节点如下
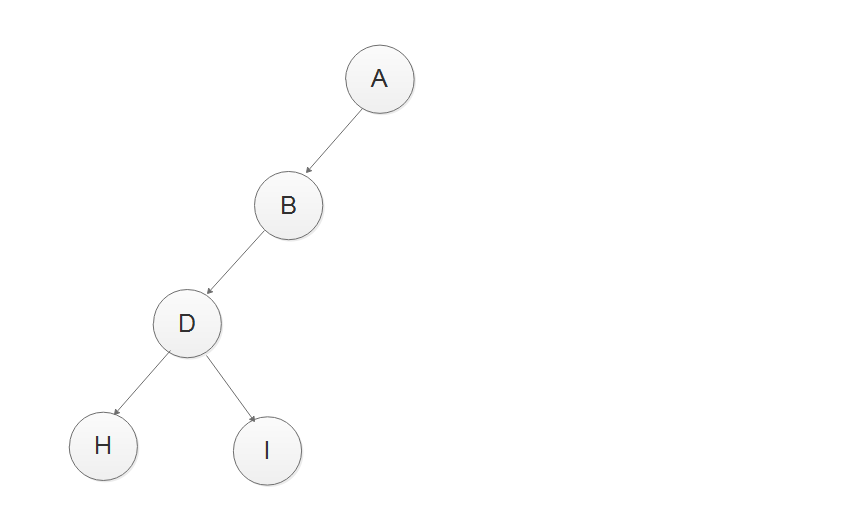
4、根据前序遍历结果,ABDHI EJKCFLMGNO,
E为JEK子树的根节点,根据第二步,这个子树的父节点是B,
根据中序遍历结果JEK,可知,J为这个子树的左节点,K为这个子树的右节点。
可添加节点如下
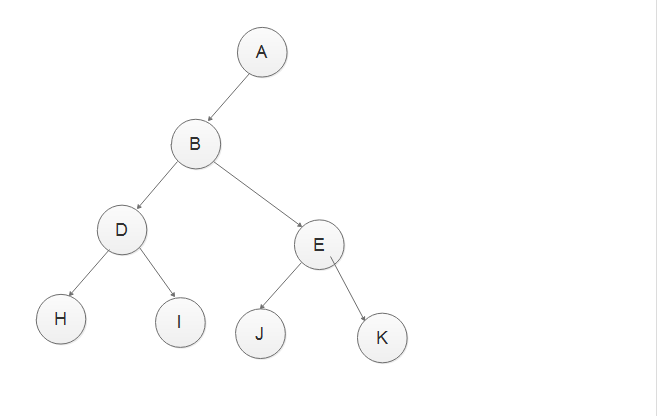
5、根据第一步划分的左子树HDIBJEK已经处理完成,继续处理右子树LFMCNGO
根据前序遍历结果ABDHIEJK CFLMGNO,可知C作为右子树LFMCNGO的根节点

6、根据中序遍历结果LFMCNGO,将这个子树再次分为LFM和NGO两个子树,
先处理左子树LFM,根据前序遍历结果可知F是这个子树的根节点,
则L为左节点,M为右节点
添加节点如下
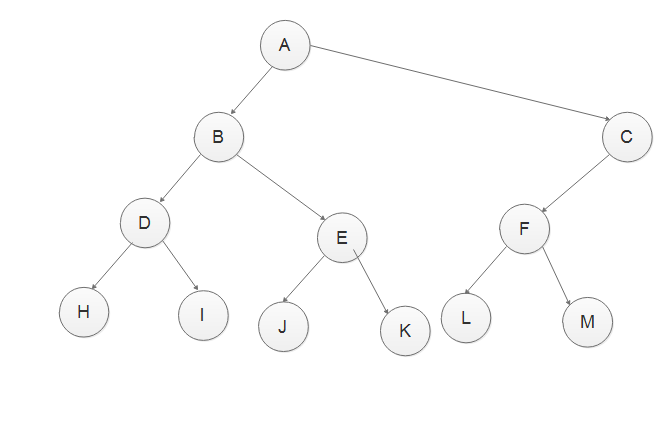
7、处理完LFM,继续处理C作为父节点的右子树NGO,根据前序遍历结果GNO可知,G作为这个子树的根节点
则N作为左节点,O作为右节点,则添加节点如下
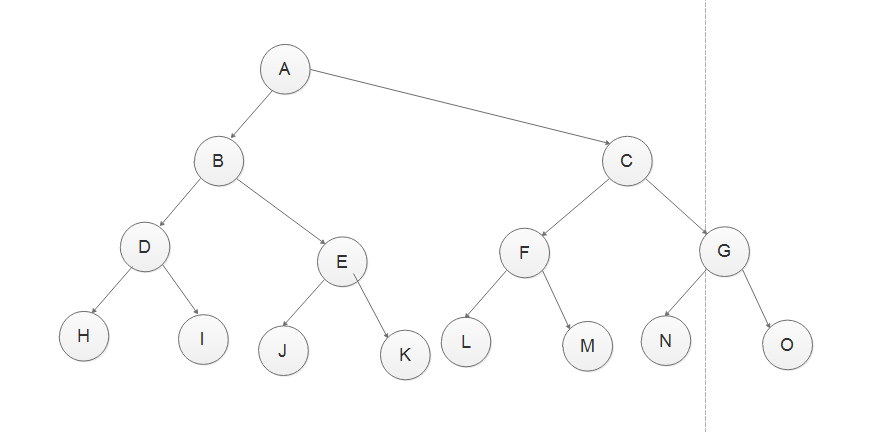
完成二叉树图。
posted on 2020-07-03 23:36 Nicholas-- 阅读(584) 评论(0) 收藏 举报



 浙公网安备 33010602011771号
浙公网安备 33010602011771号