算法漫游指北（第十二篇）:二分查找、树、树的相关概念、树的种类

一、二分查找

二分查找又称折半查找，优点是比较次数少，查找速度快，平均性能好；其缺点是要求待查表为有序表，且插入删除困难。因此，折半查找方法适用于不经常变动而查找频繁的有序列表。

二分查找操作的数据集是一个有序的数据集。开始时，先找出有序集合中间的那个元素。如果此元素比要查找的元素大，就接着在较小的一个半区进行查找；反之，如果此元素比要找的元素小，就在较大的一个半区进行查找。在每个更小的数据集中重复这个查找过程，直到找到要查找的元素或者数据集不能再分割。

二分查找的实现与分析

二分查找法实质上是不断地将有序数据集进行对半分割，并检查每个分区的中间元素。在以下介绍的实现方法中，有序数据集存放在sorted中，sorted是一块连续的存储空间。参数target是要查找的数据。

此实现过程的实施是通过变量left和right控制一个循环来查找元素（其中left和right是正在查找的数据集的两个边界值）。首先，将left和right分别设置为0和size-1。在循环的每次迭代过程中，将middle设置为left和right之间区域的中间值。如果处于middle的元素比目标值小，将左索引值移动到middle后的一个元素的位置上。即下一组要搜索的区域是当前数据集的上半区。如果处于middle的元素比目标元素大，将右索引值移动到middle前一个元素的位置上。即下一组要搜索的区域是当前数据集的下半区。随着搜索的不断进行，left从左向右移，right从右向左移。一旦在middle处找到目标，查找将停止；如果没有找到目标，left和right将重合。

二分查找图示

动图

二分法查找实现

非递归方式实现

# 非递归方式
def binary_search(nums,target):

    if len(nums) == 0:
        return False
    left = 0 
    right = len(nums) - 1
    while left <= right:
        middle = (left + right)//2
        if nums[middle] == target:
            return True
        elif nums[middle] < target:
            left = middle + 1
        elif nums[middle] > target:
            right = middle - 1
    return False

li = [10,14,21,38,45,47,53,81,86,99]        
print(binary_search(li,47))
print(binary_search(li,9))

递归方式实现

def binary_search(nums,target):
    n = len(nums)
    if n > 0:
        middle = len(nums) // 2
        if nums[middle] == target:
            return True
        elif nums[middle] > target:
            return binary_search(nums[:middle],target)
        elif nums[middle] < target:
            return binary_search(nums[middle+1:],target)
    return False

二分查找复杂度

时间复杂度

最优时间复杂度：O(1)
最坏时间复杂度：O(logn)

二分查找虽然性能比较优秀，但应用场景也比较有限。底层必须依赖数组，并且还要求数据是有序的。对于较小规模的数据查找，我们直接使用顺序遍历就可以了，二分查找的优势并不明显。二分查找更适合处理静态数据，也就是没有频繁的数据插入、删除操作。

二、树

树的定义

树（英语：tree）是一种抽象数据类型（ADT）或是实作这种抽象数据类型的数据结构，用来模拟具有树状结构性质的数据集合。它是由n（n>=1）个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

举个例子，每个人都有家族树，家族树一般长这样：

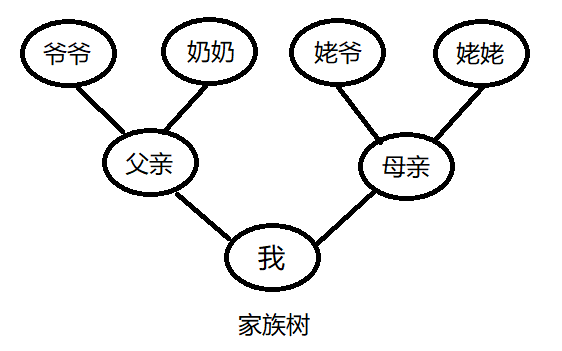
家族树的样子看起来像一颗正常的树，而数据结构中的树则像是一颗倒过来的树：

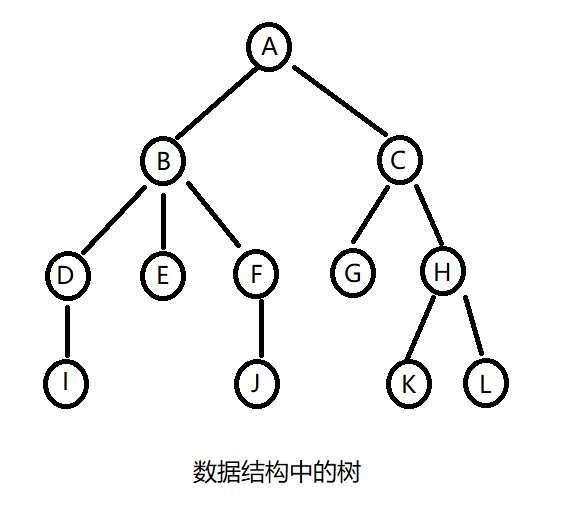
可以看出，一棵树有多个节点，上图中带〇的字母就是一个节点。

它具有以下的特点：

每个节点有零个或多个子节点；
没有父节点的节点称为根节点；
每一个非根节点有且只有一个父节点；
除了根节点外，每个子节点可以分为多个不相交的子树；

树的相关概念术语

1)节点<node> 树中每个元素都叫节点
2)根节点或树根<root> 树顶端的节点称之为根节点，也叫树根
3)子树<subTree> 除根节点之外，其他节点可以分为多个树的集合，叫做子树，在上图中，K这个节点可以称之为一颗子树，而H、K、L三个节点组合起来也可以叫做一颗子树
4)节点的度一个节点直接含有的子树的个数，称之为节点的度。比如上图中B节点的度为3，C节点的度是2，I、J、K、L节点的度是0
5)叶子节点、叶节点、终端节点度为0的节点叫做叶子节点，也叫叶节点、终端节点，其实就是没有子节点的节点，或者说没有子树的节点
6)双亲节点、父节点父节点就是一个节点上头的那个节点，如果一个节点包含若干子节点，那么这个节点就是这些子节点的父节点，也叫双亲节点
7)兄弟节点拥有相同父节点的节点互称为兄弟节点
8)树的度一棵树中最大节点的度称之为树的度，即树中哪个节点的子节点最多，那么这个节点的度也就是树的度
9)节点的层次

从根这一层开始，根算1层，根的子节点算2层，一直到最下面一层
10)树的高度、深度树的深度是从根节点开始、自顶向下逐层累加（根节点的高度是1）助记：深度从上到下树的高度是从叶节点开始、自底向上逐层累加（叶节点的高度是1）助记：高度由下向上虽然树的高度和深度一样，但是具体到某个节点上，其高度和深度通常是不一样的。
11)堂兄弟节点堂兄弟节点是同一层，父节点不同，或者说双亲节点在同一层的节点称之为堂兄弟节点
12)节点的祖先从根节点到某一节点一路顺下来的除了该节点的所有节点都是该节点的祖先节点
13)节点的子孙以某节点为根的子树中，任何一个节点都是其子孙，也就是说这个节点下面与这个节点有关的节点都是这个节点的子孙
14)森林由m棵不相交的树组成的集合，叫做森林

树的种类

无序树：树中任意节点的子节点之间没有顺序关系，这种树称为无序树，也称为自由树；
有序树

：树中任意节点的子节点之间有顺序关系，这种树称为有序树；
- 二叉树：每个节点最多含有两个子树的树称为二叉树；
  - 完全二叉树：对于一颗二叉树，假设其深度为d(d>1)。除了第d层外，其它各层的节点数目均已达最大值，且第d层所有节点从左向右连续地紧密排列，这样的二叉树被称为完全二叉树，其中满二叉树的定义是所有叶节点都在最底层的完全二叉树;
  - 平衡二叉树（AVL树）：当且仅当任何节点的两棵子树的高度差不大于1的二叉树；
  - 排序二叉树（二叉查找树（英语：Binary Search Tree），也称二叉搜索树、有序二叉树）；
- 哈夫曼树（用于信息编码）：带权路径最短的二叉树称为哈夫曼树或最优二叉树；
- B树：一种对读写操作进行优化的自平衡的二叉查找树，能够保持数据有序，拥有多余两个子树。

树的存储与表示

顺序存储：

将数据结构存储在固定的数组中，然在遍历速度上有一定的优势，但因所占空间比较大，是非主流二叉树。二叉树通常以链式存储。

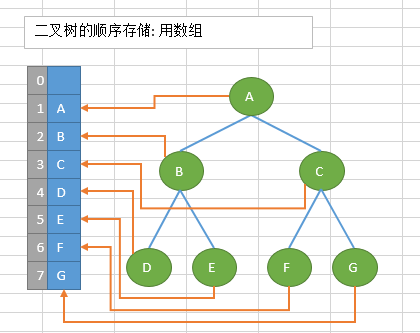
将树按照从根到叶节点，从左到右的顺序依次存储到数组里。

链式存储：

将树的数据结构存储到链表中，由于对节点的个数无法掌握，常见树的存储表示都转换成二叉树进行处理，子节点个数最多为2。

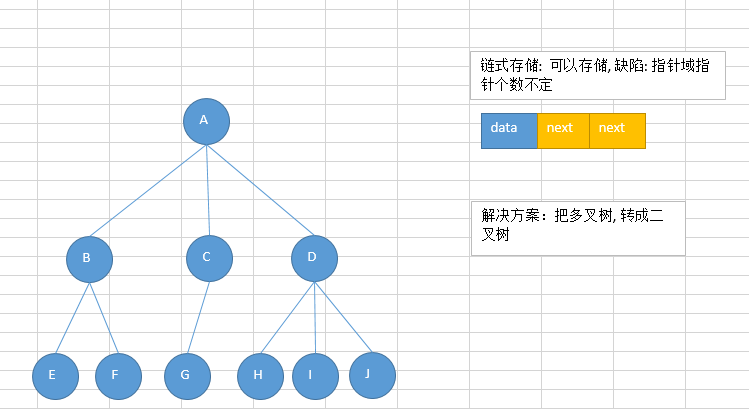
常见的一些树的应用场景

xml，html等，那么编写这些东西的解析器的时候，不可避免用到树
路由协议就是使用了树的算法
mysql数据库索引
文件系统的目录结构
所以很多经典的AI算法其实都是树搜索，此外机器学习中的decision tree也是树结构

参考资料

[1]https://www.cnblogs.com/idreamo/p/9000762.html

[2]https://segmentfault.com/a/1190000014741176

posted on 2020-06-30 23:24 Nicholas-- 阅读(821) 评论(0) 编辑收藏举报

刷新页面返回顶部

Nicholas--Altshuler