算法漫游指北（第八篇）插入排序算法描述、动图演示、代码实现、过程分析、时间复杂度和希尔排序算法描述、动图实现、代码实现、过程分析、时间复杂度

一、插入排序

插入排序（英语：Insertion Sort）是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

算法描述

一般来说，插入排序都采用in-place在数组上实现。具体算法描述如下：

从第一个元素开始，该元素可以认为已经被排序；
取出下一个元素，在已经排序的元素序列中从后向前扫描；
如果该元素（已排序）大于新元素，将该元素移到下一位置；
重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；
将新元素插入到该位置后；
重复步骤2~5。

选择排序动图演示

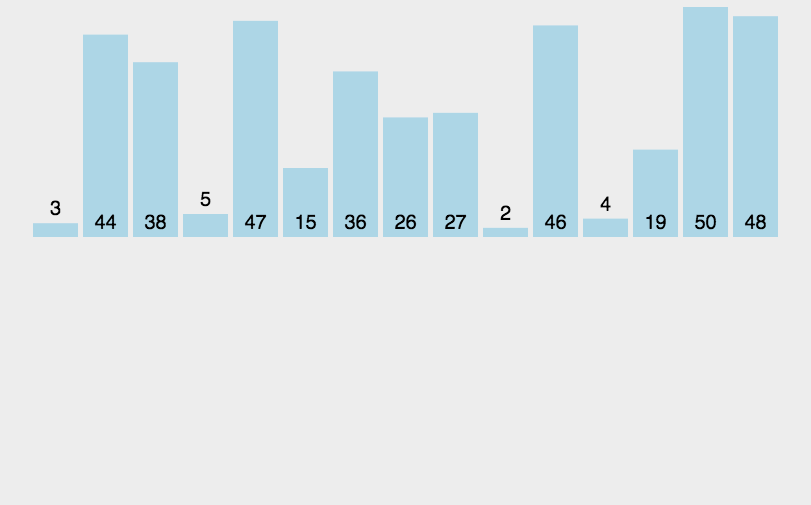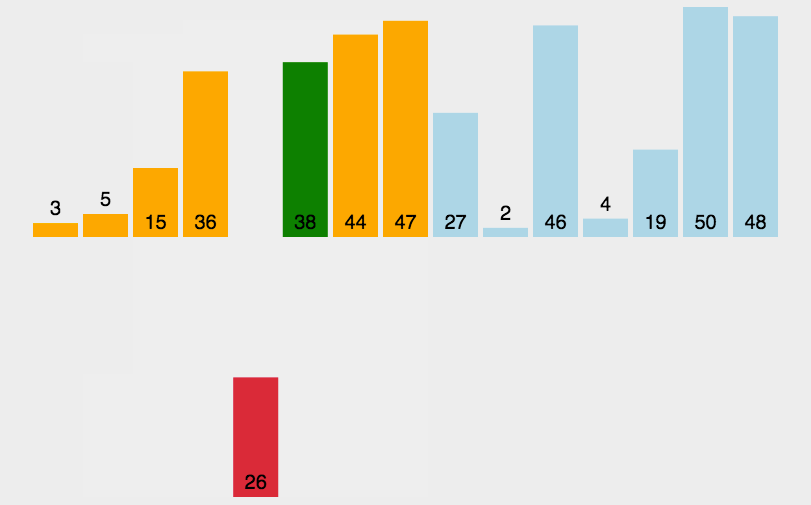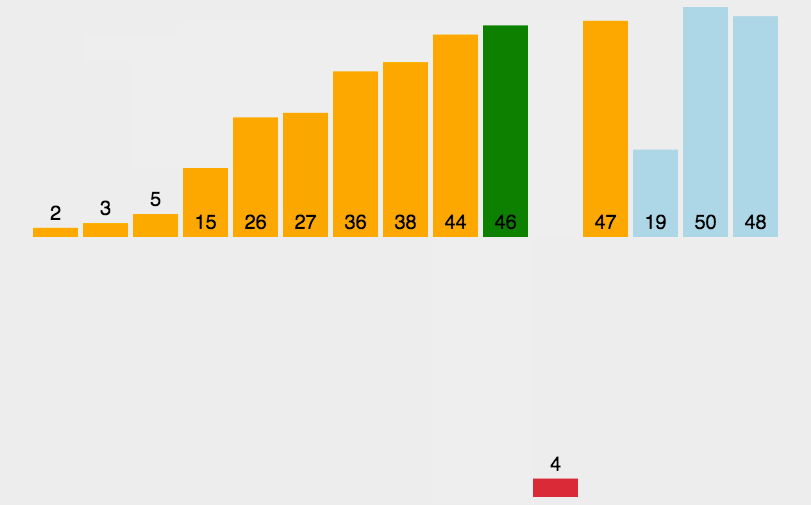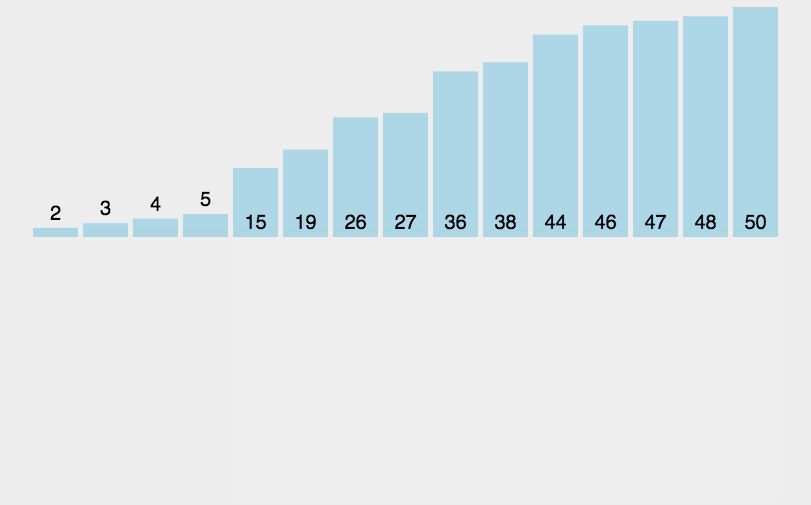
选择排序代码实现

def insert_sort(alist):
    """插入排序"""
    n = len(alist)
    # 从右边的无序序列中取出多少个元素执行这样的过程
    for j in range(1, n):
        # j = [1, 2, 3, n-1]
        # i 代表内层循环起始值
        i = j
        # 执行从右边的无序序列中取出第一个元素，即i位置的元素，然后将其插入到前面的正确位置中
        while i > 0:
            if alist[i] < alist[i-1]:
                alist[i], alist[i-1] = alist[i-1], alist[i]
                i -= 1
            else:
                break

选择排序过程分析

待排序：　　　　[49,38,65,97,76,13,27,49]

这里就是内层的while循环，进行比较大小，交换位置。

1、第1个元素和第0个元素进行比较，第1个元素（38）与之前的元素进行比较，发现38较小，进行交换

[38,49,65,97,76,13,27,49]

2、第2个元素（65）和之前的元素38，49进行比较，65大，不用交换位置，break

[38,49,65,97,76,13,27,49]

3、第3个元素97和之前的元素38，49，65进行比较，97比较大，不用交换，break

[38,49,65,97,76,13,27,49]

4、第4个元素76与97进行比较，76小，交换位置

[38,49,65,76,97,13,27,49]

76与之前的65进行比较，76大，不用交换位置，break

[38,49,65,76,97,13,27,49]

5、第五个元素13与之前的元素进行比较，

13与97比较，13小，交换位置

[38,49,65,76,13,97,27,49]

13与76比较，13小，交换位置

[38,49,65,13,76,97,27,49]

13与65比较，13小，交换位置

[38,49,13,65,76,97,27,49]

13与49进行比较，13小，交换位置

[38,13,49,65,76,97,27,49]

13与38进行比较，13小，交换位置

[13,38,49,65,76,97,27,49]

最后完成第五个元素13的插入过程

6、进行第6个元素27插入过程，与上面类似

得到结果

[13,27,38,49,65,76,97,49]

7、进行第7个元素49插入过程，与上面类似

得到结果

[13,27,38,49,49,65,76,97]

分析：

        while i > 0:
            if alist[i] < alist[i-1]:
                alist[i], alist[i-1] = alist[i-1], alist[i]
                i -= 1
            else:
                break

上面执行具体过程是执行的内层while循环，这里内层循环执行直到i=0，

但是遇到要插入的元素比最后一个已经确定的元素值还大，那么就可以直接break，结束循环，节省了时间。

外层循环要循环整个列表的长度，以保证每个元素都进行插入操作。

插入排序时间复杂度

最优时间复杂度：O(n) （升序排列，序列已经处于升序状态）
最坏时间复杂度：O(n^2)
稳定性：稳定

二、希尔排序（Shell Sort）

希尔排序按其设计者希尔（Donald Shell）的名字命名，该算法由1959年公布。第一个突破O(n2)的排序算法，是简单插入排序的改进版。它与插入排序的不同之处在于，它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。

希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因DL．Shell于1959年提出而得名。希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

算法描述

先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，具体算法描述：

选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；
按增量序列个数k，对序列进行k 趟排序；
每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m 的子序列，分别对各子表进行直接插入排序。仅增量因子为1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

希尔排序动图实现

希尔排序代码实现

def shell_sort(alist):
    """希尔排序"""

    n = len(alist)
    gap = n // 2
    
    # gap变化到0之前，插入算法执行的次数
    while gap > 0:
        # 插入算法，与普通的插入算法的区别就是gap步长
        for j in range(gap, n):
            i = j
            while i > 0:
                if alist[i] < alist[i-gap] and i-gap >= 0:
                    #注意and i-gap >= 0条件
                    alist[i], alist[i-gap] = alist[i-gap], alist[i]
                    i -= gap
                else:
                    break
        # 缩短gap步长
        gap //= 2

希尔排序过程分析

希尔排序首先选择一个元素选择步长将数组划分为若干小组，对各个小组分别进行排序，然后不断将步长缩小，不断分组和排序，直到后的步长为1，对所有的元素进行排序，此时，经过前期的排序工作，能够减少全体元素插入排序的对比次数，大大降低了排序的时间复杂度。

假设有这样一组数

li=[68,17,88,98,19,1,12,53,93,6,79,2,25,15,11,73,20,5,33,75,51,38,26,24,56,

36,61,60,36,27,80,66,76,6,56,29,23,14,44,21,15,59,60,33,14,41,87,47,89,80]

使用默认的n/2步长序列进行希尔排序

1、

第一遍

步长为gap = len(li)//2 = 25

将第0个元素和第25个元素68，36取出来进行比较，36小，与第0个元素进行交换

列表变为

[36,17,88,98,19,1,12,53,93,6,79,2,25,15,11,73,20,5,33,75,51,38,26,24,56,68，

61,60,36,27,80,66,76,6,56,29,23,14,44,21,15,59,60,33,14,41,87,47,89,80]

将第1个元素和第26个元素17，61进行比较，61大，不用互换位置

将第2个元素和第27个元素88，60进行比较，60小，互换位置

列表变为

[36,17,60,98,19,1,12,53,93,6,79,2,25,15,11,73,20,5,33,75,51,38,26,24,56,68，61,88,36,27,80,66,76,6,56,29,23,14,44,21,15,59,60,33,14,41,87,47,89,80]

... ...

依次类推，直到完成

第25个元素和第50个元素56，80进行比较，

第一遍比较互换位置后，

此时列表为

[36, 17, 60, 36, 19, 1, 12, 53, 6, 6, 29, 2, 14, 15, 11, 15, 20, 5, 33, 14, 41, 38, 26, 24, 56,

68, 61, 88, 98, 27, 80, 66, 76, 93, 56, 79, 23, 25, 44, 21, 73, 59, 60, 33, 75, 51, 87, 47, 89, 80]

可以看出列表已经有了一定的顺序

2、第二遍

gap =gap//2 = 12

将第0个元素、第12个元素,、第24个元素、第36个元素、第48个元素取出来

36，14，56，23，89取出来进行插入排序

得到结果

[14, 17, 60, 36, 19, 1, 12, 53, 6, 6, 29, 2,23, 15, 11, 15, 20, 5, 33, 14, 41, 38, 26, 24, 36,

68, 61, 88, 98, 27, 80, 66, 76, 93, 56, 79, 56, 25, 44, 21, 73, 59, 60, 33, 75, 51, 87, 47, 89, 80]

将第1个元素、第13个元素、第25个元素、第37个元素、第49个元素取出来

17，15，68，25，80进行插入排序

得到结果

[14, 15, 60, 36, 19, 1, 12, 53, 6, 6, 29, 2,23, 17, 11, 15, 20, 5, 33, 14, 41, 38, 26, 24, 36,

25, 61, 88, 98, 27, 80, 66, 76, 93, 56, 79, 56, 68, 44, 21, 73, 59, 60, 33, 75, 51, 87, 47, 89, 80]

以此类推，直到完成

第11个元素、第23个元素、第35个元素、第47个元素2，24，79，47进行比较，

第二遍比较插入排序互换位置后，

此时列表为

[14, 15, 11, 15, 19, 1, 12, 14, 6, 6, 26, 2, 23, 17, 44, 21, 20, 5, 33, 33, 41, 38, 29, 24, 36, 25, 60, 36, 73, 27, 60, 53, 75, 51, 56, 47, 56, 68, 61, 88, 98, 59, 80, 66, 76, 93, 87, 79, 89, 80]

3、gap =gap //2 = 6

与上面类似，进行插入排序

得到列表为

[12, 14, 6, 6, 19, 1, 14, 15, 11, 15, 20, 2, 23, 17, 41, 21, 26, 5, 33, 25, 44, 36, 29, 24, 36, 33, 60, 38, 56, 27, 56, 53, 61, 51, 73, 47, 60, 66, 75, 88, 87, 59, 80, 68, 76, 93, 98, 79, 89, 80]

4、gap = 3

与上面类似，进行插入排序

得到列表为

[6, 14, 1, 12, 15, 2, 14, 17, 5, 15, 19, 6, 21, 20, 11, 23, 25, 24, 33, 26, 27, 36, 29, 41, 36, 33, 44, 38, 53, 47, 51, 56, 59, 56, 66, 60, 60, 68, 61, 80, 73, 75, 88, 80, 76, 89, 87, 79, 93, 98]

5、gap =1

与上面类似，进行插入排序

得到列表为

[1, 2, 5, 6, 6, 11, 12, 14, 14, 15, 15, 17, 19, 20, 21, 23, 24, 25, 26, 27, 29, 33, 33, 36, 36, 38, 41, 44, 47, 51, 53, 56, 56, 59, 60, 60, 61, 66, 68, 73, 75, 76, 79, 80, 80, 87, 88, 89, 93, 98]

希尔排序时间复杂度：

在最优的情况下，根据步长序列的不同而不同,

步长为n/2最优时间复杂度为：O（n ^ (1.3) ）（经数学统计验证）

在最差的情况下，时间复杂度为：O（n ^ 2）；

空间复杂度：

O(1)

希尔排序没有快速排序算法快 O(n(logn))，因此中等大小规模表现良好，对规模非常大的数据排序不是最优选择。但是比O()复杂度的算法快得多。并且希尔排序非常容易实现，算法代码短而简单。

此外，希尔算法在最坏的情况下和平均情况下执行效率相差不是很多，与此同时快速排序在最坏的情况下执行的效率会非常差。专家们提倡，几乎任何排序工作在开始时都可以用希尔排序，若在实际使用中证明它不够快，再改成快速排序这样更高级的排序算法.

本质上讲，希尔排序算法是直接插入排序算法的一种改进，减少了其复制的次数，速度要快很多。原因是，当n值很大时数据项每一趟排序需要移动的个数很少，但数据项的距离很长。当n值减小时每一趟需要移动的数据增多，此时已经接近于它们排序后的最终位置。正是这两种情况的结合才使希尔排序效率比插入排序高很多。Shell算法的性能与所选取的分组长度序列有很大关系。

希尔排序中对于增量序列的选择十分重要，直接影响到希尔排序的性能。我们上面选择的增量序列{n/2,(n/2)/2...1}(希尔增量gap)，其最坏时间复杂度依然为O(n^2)，一些经过优化的增量序列如Hibbard经过复杂证明可使得最坏时间复杂度为O(n^3/2)。

步长序列

步长的选择是希尔排序的重要部分。只要最终步长为1任何步长序列都可以工作。算法最开始以一定的步长进行排序。然后会继续以一定步长进行排序，最终算法以步长为1进行排序。当步长为1时，算法变为普通插入排序，这就保证了数据一定会被排序。

Donald Shell最初建议步长选择为为n/2,并且对步长取半直到步长达到1。虽然这样取可以比O(n^2)类的算法（插入排序）更好，但这样仍然有减少平均时间和最差时间的余地。

已知的最好步长序列是由Sedgewick提出的(1, 5, 19, 41, 109,...)

Sedgewick 增量序列的通项公式为：

h_i = max (9 * 4^j - 9 * 2^j + 1, 4^k - 3 * 2^k + 1)

Sedgewick 增量序列的最坏时间复杂度为 O(N^4/3)O(N^4/3)；平均时间复杂度约为 O(N^7/6)O(N^7/6)。

参考资料

[1]https://www.cnblogs.com/onepixel/p/7674659.html

[2]https://blog.csdn.net/rosyhuan/article/details/77944478

posted on 2020-06-06 23:56 Nicholas-- 阅读(467) 评论(0) 编辑收藏举报

刷新页面返回顶部

Nicholas--Altshuler