算法漫游指北（第六篇）双端队列、排序算法分类、排序算法的稳定性、排序算法复杂度

一、双端队列

双端队列

双端队列（deque，全名double-ended queue），是一种具有队列和栈的性质的数据结构。

双端队列中的元素可以从两端弹出，其限定插入和删除操作在表的两端进行。双端队列可以在队列任意一端入队和出队。

 

双端队列（Deque），是一种类似于队列的元素的有序集合。它拥有两端，队首和队尾，并且元素保持在当前的位置。双端队列的一个不同点就是，添加和删除元素的位置不受限制。新元素可以在队首或者队尾添加。同样地，双端队列中的元素可以从两端弹出。在某种意义上，这种混合的线性结构同时具有栈和队列的性质。

 

 

方法

• Deque() 创建一个空的双端队列

• add_front(item) 从队头加入一个item元素

• add_rear(item) 从队尾加入一个item元素

• remove_front() 从队头删除一个item元素

• remove_rear() 从队尾删除一个item元素

• is_empty() 判断双端队列是否为空

• size() 返回队列的大小

 

Python实现双端队列

在Python中，有两种方式可以实现上述的双端队列ADT：使用内建类型list、使用标准库collections.deque（其实collections.deque就是Python中双端队列的标准实现）。

两种方式的不同主要体现在性能上（具体参考 collections.deque | TimeComplexity）：

用列表实现双端队列

class Deque(object):
    """双端队列"""
    def __init__(self):
        self.items = []
 
    def is_empty(self):
        """判断队列是否为空"""
        return self.items == []
 
    def add_front(self, item):
        """在队头添加元素"""
        self.items.insert(0,item)
 
    def add_rear(self, item):
        """在队尾添加元素"""
        self.items.append(item)
 
    def remove_front(self):
        """从队头删除元素"""
        return self.items.pop(0)
 
    def remove_rear(self):
        """从队尾删除元素"""
        return self.items.pop()
 
    def size(self):
        """返回队列大小"""
        return len(self.items)
 
if __name__ == "__main__":
    deque = Deque()
    deque.add_front(1)
    deque.add_front(2)
    deque.add_rear(3)
    deque.add_rear(4)
    print('队列长度',deque.size())
    print(deque.remove_front())
    print(deque.remove_front())
    print(deque.remove_rear())
    print(deque.remove_rear())
    print('队列长度',deque.size())
​

　　

分析：list作为容器，在双端队列的任何一端执行添加（append）和删除(pop)操作,时间复杂度为O(1),

但是当list遇到pop(0)和insert(0, v)这样既改变了列表的长度又改变其元素位置的操作时，其时间复杂度变为O(n)了。

 

使用标准库collections.deque

Python的deque模块，它是collections库的一部分。deque实现了双端队列，意味着你可以从队列的两端加入和删除元素。

append(x)：把元素x添加到队列的右端
appendleft(x)：把元素x添加到队列的左端
pop()：移除并返回deque右端的元素，如果没有元素抛IndexError
popleft()：移除并返回deque左端的元素，如果没有元素抛IndexError
​
​
index(x[, start[, stop]])：返回x元素在队列中的索引，放回第一个匹配，如果没有找到抛ValueError
insert(i, x)：在队列的i索引处，插入x元素
remove(value)：删除第一个匹配value的元素，如果没有找到抛ValueError
​
​
clear()：清空队列中所有元素
copy()：创建队列的浅拷贝
count(x)：计算队列中等于x元素的个数
​
extend(iterable)：在队列右端通过添加元素扩展
extendleft(iterable)：在队列左端通过添加元素扩展
​
reverse()：在原地反转队列中的元素
rotate(n)：把队列左端n个元素放到右端，如果为负值，右端到左端。如果n为1，等同d.appendleft(d.pop())
maxlen：只读属性，队列中的最大元素数

　　

简单示例

​
​

from collections import deque
​
# 实例化一个deque对象
d = deque()
​
# 在队列尾插入元素
d.append(1)
d.append(2)
d.append(3)
d.append(4)
print(d)  #deque([1, 2, 3, 4])
​
# 在队列头插入元素
d.appendleft(5)
print(d)      # deque([5, 1, 2, 3, 4])
​
# 长度
print(len(d)) #5
# 队列按索引取值
print(d[0])   #5
print(d[-1])  #4
​
print('-'*10)
​
#在右侧删除一个元素
d.pop()
print(d)      # deque([5, 1, 2, 3])
​
# 在左侧删除一个元素
d.popleft()
print(d)      # deque([1, 2, 3])
​
# 扩展元素,类似列表的扩展，直接通过列表进行扩展，在deque右端插入多个元素
d.extend([4,5,6])
print(d)    # deque([1, 2, 3, 4, 5, 6])
​
# 扩展元素，在deque左端插入多个元素，注意最后插入元素的顺序与插入的列表相反
d.extendleft([7,8,9])
print(d)    # deque([9, 8, 7, 1, 2, 3, 4, 5, 6])

　　

​

也可以重写，实现用列表方式调用形式的统一

# 使用标准库collections.deque
from collections import deque
class Deque:
​
  def __init__(self):
    self.items = deque()
​
  def addFront(self, item):
    self.items.appendleft(item)
​
  def addRear(self, item):
    self.items.append(item)
​
  def removeFront(self):
    return self.items.popleft()
​
  def removeRear(self):
    return self.items.pop()
​
  def is_empty(self):
    return self.size() == 0
​
  def size(self):
    return len(self.items)
    

　　

 

 

deque各操作时间复杂度

 

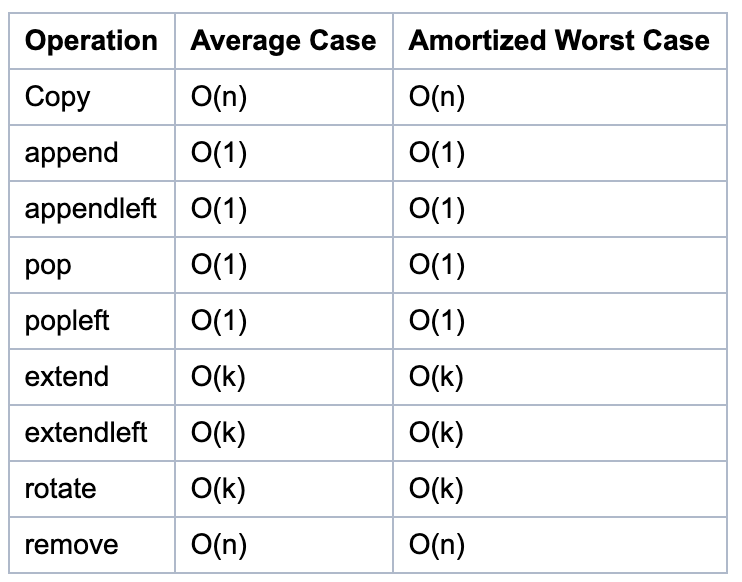
注意：pop/popleft/append/appendleft 四种操作的时间复杂度均是 O(1)。

 

 

二、排序

排序算法（英语：Sorting algorithm）是一种能将一串数据依照特定顺序进行排列的一种算法。

 

排序算法分类

1.比较类排序 通过比较来决定元素间的相对次序，由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序

2.非比较类排序（一般用于整型相关的数据类型） 不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此也称为线性时间非比较类排序。

 

 

排序算法的稳定性

稳定性：稳定排序算法会让原本有相等键值的纪录维持相对次序。也就是如果一个排序算法是稳定的，当有两个相等键值的纪录R和S，且在原本的列表中R出现在S之前，在排序过的列表中R也将会是在S之前。

稳定性的意思是对于序列中键值（Key value）相同的元素，它们在排序前后的相对关系保持不变。对于int这样的基本数据类型，稳定性基本上是没有意义的，因为它的键值就是元素本身，两个元素的键值相同他们就可以被认为是相同的。但对于复杂的数据类型，数据的键值相同，数据不一定相同，比如一个Student类，包括Name和Score两个属性，以Score为键值排序，这时候键值相同元素间的相对关系就有意义了。

 

当相等的元素是无法分辨的，比如像是整数，稳定性并不是一个问题。然而，假设以下的数对将要以他们的第一个数字来排序。

(4, 1)  (3, 1)  (3, 7)（5, 6）

在这个状况下，有可能产生两种不同的结果，一个是让相等键值的纪录维持相对的次序，而另外一个则没有：

(3, 1)  (3, 7)  (4, 1)  (5, 6)  （维持次序）
(3, 7)  (3, 1)  (4, 1)  (5, 6)  （次序被改变）

不稳定排序算法可能会在相等的键值中改变纪录的相对次序，但是稳定排序算法从来不会如此。不稳定排序算法可以被特别地实现为稳定。做这件事情的一个方式是人工扩充键值的比较，如此在其他方面相同键值的两个对象间之比较，（比如上面的比较中加入第二个标准：第二个键值的大小）就会被决定使用在原先数据次序中的条目，当作一个同分决赛。然而，要记住这种次序通常牵涉到额外的空间负担。

 

 

 

排序算法复杂度

 

初级排序（O(n^2)时间复杂度）

1.选择排序

每次找最小值，然后放到待排序数组的起始位置

2.插入排序 从前到后 逐步构建有序序列；对于未排序的数列，在已排序序列中从后向前扫描，找到相应位置并插入。

3.冒泡排序 嵌套循环，每次查看相邻元素，如果逆序，那么交换、

 

 

高级排序（O(nlogn)时间复杂度，重点考察）

• 快速排序 数组取标杆pivot，将小元素放pivot左边，大元素放右边，然后，依次对左边和右边的子数组继续快排；以到达这个序列有序。

• 归并排序（分治思想） 1.把长度为n的输入序列分成两个长度为n/2的子序列 2.对这两个子序列分别采用归并排序 3.将两个排序好的子序列合并成一个最终的排序序列。

归并与快排具有相似性，但步骤顺序相反。

归并：先排序左右子数组，然后合并两个有序子数组 快排：先调配出左右子数组，然后对于左右子数组进行排序

 

• 堆排序

  • 堆插入O(logN)，取最大/小值O(1) 1.数组元素依次建立小顶堆 2.依次取栈顶元素，并删除

 

其他排序（了解）

• 计数排序 计数排序要求输入的数据必须是有确定范围的整数。将输入的数据值转化为键存储在额外开辟的数组空间中；然后依次把计数大于1的填充回原数组。

• 桶排序 桶排序的工作原理：假设输入数据服从均匀分布，将数据分到有限数量的桶里面，每个桶在分别排序。

• 基数排序 基数排序是按照低为先排序，然后收集，再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序的，再按高优先级排序。

   

   

 

参考资料

[1]https://www.cnblogs.com/onepixel/p/7674659.html