[luogu5022][NOIP2018] 旅行
这个思路在考场上就想出来了,但是没有写出来很可惜。
对于一棵树来说,求其最小字典序的dfs序非常简单,每次从小到大遍历出边即可。对于边我们考虑事先进行排序,然后再插入到邻接表里。时间复杂度为\(O(N\log N)\)
对于一个图,并且\(N=M\),就可以保证有且只有一个环。那么会出现一种神奇的情况,如果按照树的做法进行dfs:
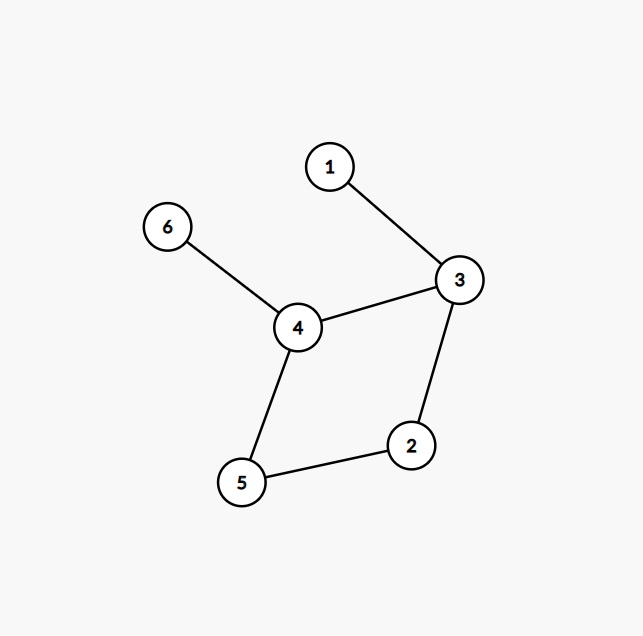
你的dfs序是132546,但是答案是132456,也就是在2-5这里,直接返回了,从环的另一短继续遍历。
这个过程可以理解为:把2-5这条边删了,然后跑树的遍历
所以我们考虑枚举删边,然后进行dfs
但是会超时啊……所以需要剪枝:当前的dfs序和之前的比已经不会更优了,就直接退出
#include <cstdio>
#include <cstring>
#include <algorithm>
#define MAXN 5005
struct edge {
int u,v;
}E[MAXN],A[MAXN<<1];
struct table {
int v,next;
}G[MAXN<<1];
int head[MAXN];
bool vis[MAXN];
int ans[MAXN],temp[MAXN];
int N,M,tot = 0;
inline int read() {
int num = 0; char ch = getchar();
while(ch<'0'||ch>'9') ch = getchar();
while(ch>='0'&&ch<='9') num = num*10+ch-48,ch = getchar();
return num;
}
inline void add(int u,int v) {
G[++tot].v = v; G[tot].next = head[u]; head[u] = tot;
}
int step = 1;
int flag = 0;
void dfs(int u,int opt,int fa) {
if(ans[step]==0) ans[step] = u;
else if(ans[step]>u) ans[step] = u,flag = 1;
else if(flag==1) ans[step] = u;
else if(ans[step]==u);
else if(ans[step]<u) {
flag = -1;
return;
}
step++;
vis[u] = 1;
for(int i=head[u];i;i=G[i].next) {
int v = G[i].v;
if(v==fa||vis[v]) continue;
if(E[opt].u==u&&E[opt].v==v) continue;
if(E[opt].v==u&&E[opt].u==v) continue;
dfs(v,opt,u);
if(flag==-1) return;
}
}
inline bool cmp(edge a,edge b) {
return a.v>b.v;
}
int work(int u,int opt,int fa) {
int size = 1;
vis[u] = 1;
for(int i=head[u];i;i=G[i].next) {
int v = G[i].v;
if(v==fa||vis[v]) continue;
if(E[opt].u==u&&E[opt].v==v) continue;
if(E[opt].v==u&&E[opt].u==v) continue;
size += work(v,opt,u);
}
return size;
}
int main() {
N = read(); M = read();
for(int i=1;i<=M;++i) {
E[i].u = read(); E[i].v = read();
A[(i<<1)-1] = E[i];
A[i<<1] = (edge) {E[i].v,E[i].u};
}
std::sort(A+1,A+1+(M<<1),cmp);
for(int i=1;i<=M<<1;++i) {
add(A[i].u,A[i].v);
}
std::memset(vis,0,sizeof(vis));
std::memset(ans,0,sizeof(ans));
step = 1;
flag = 1;
if(M==N-1) dfs(1,0,1);
else {
for(int i=1;i<=M;++i) {
std::memset(vis,0,sizeof(vis));
if(work(1,i,1)!=N) continue;
std::memset(vis,0,sizeof(vis));
step = 1; flag = 0;
dfs(1,i,1);
}
}
for(int i=1;i<N;++i) printf("%d ",ans[i]);
printf("%d",ans[N]);
return 0;
}
这里再提供一种做法,虽然没写出来可能有错……
因为环只有一个,如果我们能找到环,是否只需要求出删哪条边最优就好了,那么怎么求这个最优边呢?
环上的起点一定有两条出边,那么我们先选较优的一直走下去,如果下一个点不如起点的另一个点优,那么此时就应该回溯,所以这条边就是我们要的边。

