unsigned 整型实现无溢出运算
普通的 int 整型能表示的范围很有限,所以刷题时很多时候不得不用 long long 来存更大的数据。或者找出数列中某个只出现一次(或奇数次)的数(其余的数均出现两次 / 偶数次),用异或运算的经典题目,然而,如果数据范围不大的话,O(n) 的复杂度下,把第一次出现的所有数全加 / 乘起来,然后再减 / 除去第二次出现的 n - 1 个数(缺少的那个就是要求的数),原理是可以的,只是一般 OJ 出这样的题目必然不会让你用这种小学生的思维去做,所以会把数据设置得奇大,让你一累加必然溢出,更不用说乘了;然而,我发现,用无符号的整数貌似能避免这样的问题,因为它溢出后自动环回,就像自动取模一样,比如 unsigned int,对于溢出的运算,都会将结果对 1<<32 取模(实际上我也解释不清楚,组成原理没学好 o(╯□╰)o ),我写了个类似的程序发现好像真的是这样,虽说没有严格测试过:

1 #include<cstdio> 2 #include<cstring> 3 typedef unsigned int ui; 4 const ui inf = 0x3fffffff; 5 6 int main() { 7 ui sum = 0, n, x; 8 printf("inf = %u\n",inf); 9 10 n = 300; 11 while(n--) { 12 sum += inf; 13 sum += inf / 2; 14 sum += inf - inf / 3; 15 } 16 printf("sum = %u\n",sum); 17 18 for(int i = 1; i <= 300; ++i) { 19 sum -= inf - inf / 3; 20 sum -= inf / 2; 21 sum -= inf; 22 } 23 printf("%u\n",sum); 24 25 return 0; 26 }
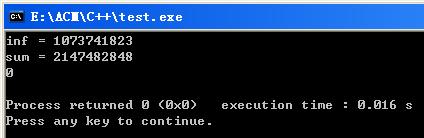
运行结果如下: