集成学习
集成学习
Category: 机器学习听课笔记
Last Edited: Nov 07, 2018 9:09 PM
Tags: 听课笔记,机器学习
集成学习(ensemble learning)概述:
- 它不是一种单独的机器学习算法,而是通过构建结合多个个体学习器(individual learner)来完成任务。又被称为多分类系统(multi-classifier)或者基于委员会的学习(committee-based learning)。
- 集成分为同质(homogeneous)集成和异质(heterogeneous)集成。同质的即集成中只包含同类的个体学习器,异质的即包含不同类的个体学习器。同质集成的个体学习器称为“基学习器”,异质集成的个体学习器称为“组件学习器”。
- 一个好的集成学习器中的个体学习器需要满足多样性和准确性。
- 多样性:个体学习器之间具有一定的差异。
- 准确性:个体学习器具有一定的准确性。
- 常见的结合策略:
-
平均法(常用于数值类的回归预测问题):
-
算术平均:对若干弱学习器的输出进行求算术平均得到最终的预测输出。

-
加权平均:给每个弱学习器一个权重ω,求其加权平均值得到最后的预测输出。
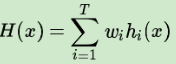
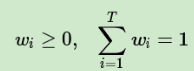
-
-
投票法(常用于分类的预测问题):
- 相对多数投票法:少数服从多数投票。
- 绝对多数投票法:在获得最高投票的同时需要票过半数。
- 加权投票法:票数✖权重,将各个类别的加权票数求和,得到的最大值为最终类别。
-
学习法:相较于上两种方法,学习法不对结果做直接的处理,而是在结果外再加一层学习器,即将各个弱学习器的结果作为输入,通过一层学习器将训练集的输出作为输出,重新学习得到一个结果。此时,弱学习器称为“初级学习器”,用于预测结果的学习器称为“次级学习器”。(数据→弱学习器(初级学习器)→次级学习器)其代表方法为:stacking
-
Stacking简介:
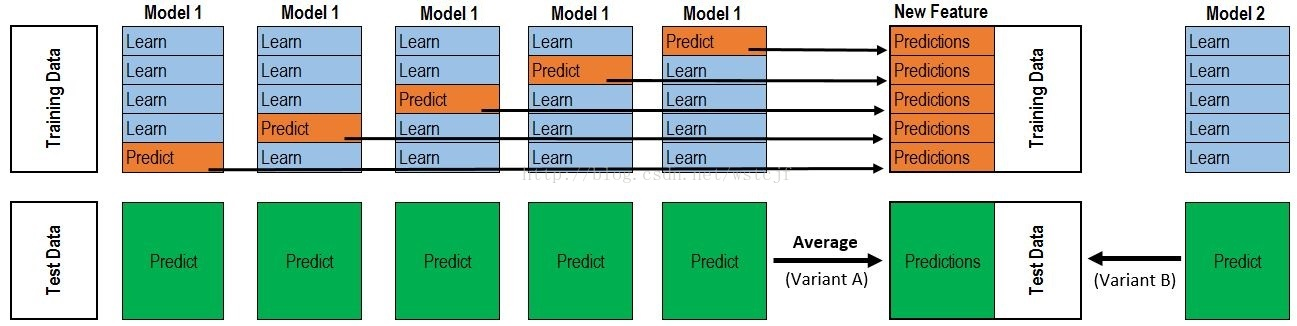
-
-
Boosting策略
-
boosting是一种集成策略,它可以将“弱学习器”提升为“强学习器”。他的特点是:个体学习器之间存在很强的依赖关系,必须串行生成序列化的方法。
- 弱学习算法:指泛化性能略优于随机猜测的分类算法
- 强学习算法:识别准确率很高并且能在多项式时间内完成的学习算法
-
boosting一族算法的基本思想:
- 提升方法主要需要解决两个问题:
-
每一轮如何改变训练数据的权值或概率分布
-
如何将弱分类器组合称为一个强分类器
先从训练集训练得到一个基学习器,再根据及学习器的表现对训练样本分布进行调整,使之前学习器中做错的训练样本在后续受到更多的关注。然后基于调整后的样本分布训练下一个基学习器。如此不断重复,直到基学习器达到事先指定的数目T,最终将这T个基学习器进行加权结合。
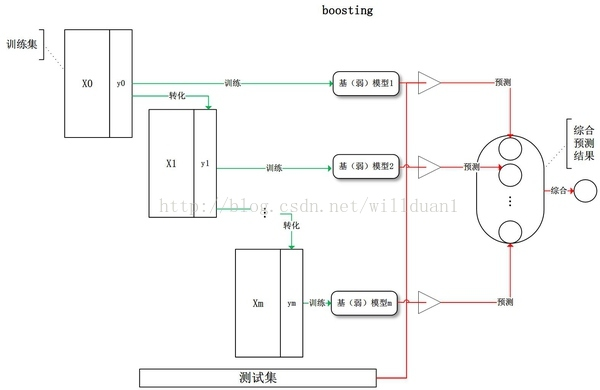
-
- 提升方法主要需要解决两个问题:
-
AdaBoost算法思想:
- 在每一轮中提高在前一轮弱分类器错误分类的样本权值,降低正确样本的权值
- 加权多数表决方法。加大误差率小的弱分类器的权值,减小误差率大的弱分类器的权值。
-
AdaBoost算法描述:
-
初始化训练数据的权值分布:
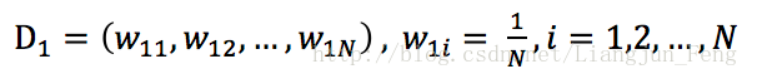
-
对数据集进行学习,得到基本分类器:
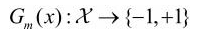
假设是一个二分类问题
-
计算Gm(x)在训练集上的分类误差率:
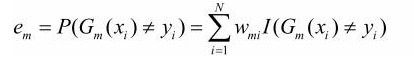
-
计算Gm(x)的系数:
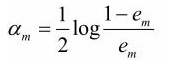
系数am表示Gm(x)在最终分类器中的重要性。按照这个计算公式,am随着em的增大而减小,说明误差率越大在最终分类器中所起的作用越小
-
更新训练数据集的权值分布:
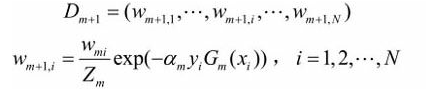
Zm是规范化因子,用于保证Dm+1是一个完整的概率分布。Wmi表示第m轮中第i个实例的权值。
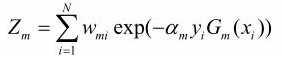
上式可以表示为:
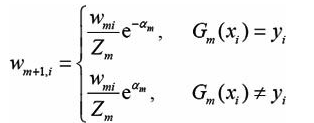
当正确分类时,Wm+1,i的值被缩小 当错误分类时,Wm+1,i的值被扩大
-
构建基本分类器的线性组合:
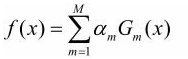
m个分类器的加权表决
-
得到最终的分类器:
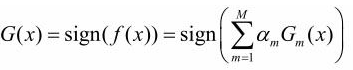
-
-
AdaBoost算法的优缺点:
- 优点:提供了一种由简单到复杂的系统思想/不需要先验知识/有效提高基分类器的精度
- 缺点:噪声数据处理效果不佳/对多分类问题没有很好的解决方案
Bagging策略
- Bagging是一种并行式的集成学习方法。在boosting中我们采用的是数据采样后从每个数据子集中训练出基学习器,并且是串行方式不断强化学习器,而Bagging采用的数据集是可以交叠的。
- Bagging策略的基本流程:
- 随机采样(自助采样→有放回),采集m个样本的采样集
- 基于每个样本训练出m个基学习器
- 将m个基学习器集合起来构成最终学习器
- 集合策略的选择:
- 分类问题→简单投票法
- 回归问题→简单平均法
- 集合策略的选择:
- Bagging策略的特点:
- 计算一个Bagging强学习器的算法复杂度和直接使用基学习器的算法复杂度同阶,效率很高。
- 相较于Boosting策略,Bagging策略可以用于多分类和回归问题。
- 由于随机采样的特性,根据随机采样公式全部样本的63.2%将会被采样。由此会得到36.8的包外数据(袋外数据)。这些包外数据可以用于:
- 包外估计(out-of-bag estimate)→估计训练器的泛化性能。
- 当基学习器是决策树时,可以用于辅助剪枝,或用于辅助对零训练样本点处理。
- 当基学习器时神经网络时,可以用于辅助早期停止来减小过拟合的风险。
随机森林算法(RandomForest)
- 随机森林算法使用决策树作为弱学习器。
- 在随机森林算法中的决策树特征选择和单决策树的特征选择有所不同,随机森林从所有特征N中随机选择n个样本,从这n个特征中选择一个最优的特征来作为决策树的划分点。这么做的好处是增强随机森林的泛化性。也就是说,n越小,随机选择的特征越少,决策树拟合就越低,随机森林越健壮。一般使用交叉验证来选择一个合适的n的值。
- 算法描述:
- 对训练集进行t次随机采样,共采集m次,得到包含m个样本的采样机Dm。
- 用采样集Dm训练出m个决策树模型Gm(x)
- 分类问题→简单投票 回归问题→算术平均


