贝叶斯分类器
贝叶斯分类器
Category: 机器学习听课笔记
Last Edited: Oct 10, 2018 9:43 PM
Tags: 听课笔记,机器学习
注:本文非完全原创,很多公式和例子借鉴于各位前辈。
先导知识

-
贝叶斯决策论:贝叶斯决策论考虑如何基于已知的概率和误判损失来选择最优的类别标记。
-
先验概率(prior probability):是指根据以往经验和分析得到的概率。即没有考虑原因,在获得数据和依据之前就对概率进行了猜测,得到了概率。
-
似然函数(likelihood function):似然用来描述已知随机变量输出结果时,未知参数的可能取值。似然函数关注的是由已知的结果和某固有属性的关系,而不是结果或者原因的概率,所以称似然是对固有属性的拟合,所以不能称之为概率。
-
后验概率(Posterior probability):是在相关证据或者背景给定并纳入考虑之后的条件概率。是由因及果的概率。
-
先验分布:根据一般的经验认为随机变量应该满足的分布
后验分布:通过当前训练数据修正的随机变量的分布,比先验分布更符合当前数据
似然估计:已知训练数据,给定了模型,通过让似然性极大化估计模型参数的一种方法
后验分布往往是基于先验分布和极大似然估计计算出来的。
-
先验、似然、后验的区分总结:
1)先验——根据若干年的统计(经验)或者气候(常识),某地方下雨的概率;
2)似然——下雨(果)的时候有乌云(因/证据/观察的数据)的概率,即已经有了果,对证据发生的可能性描述;
3)后验——根据天上有乌云(原因或者证据/观察数据),下雨(结果)的概率;
后验 ~ 先验*似然 : 存在下雨的可能(先验),下雨之前会有乌云(似然)~ 通过现在有乌云推断下雨概率(后验);
或者:
设定背景:酒至半酣,忽阴云漠漠,骤雨将至。
情景一:“天不会下雨的,历史上这里下雨的概率是20%”----先验概率“但阴云漠漠时,下雨的概率是80%”----后验概率
情景二:“飞飞别急着走啊,历史上酒桌上死人的概率只有5%“----先验概率”可他是曹操啊,梦里都杀人“----后验概率
-
最大似然估计(Maximum Likelihood Estimation):最大似然估计是利用已知的样本的结果,在使用某个模型的基础上,反推最有可能导致这样结果的模型参数值。
-
贝叶斯公式:
-
在通常情况下,“事件A在事件B发生的条件下的概率”与“事件B在事件A发生的条件下的概率”是不一样的,但两者的关系是确定的,贝叶斯公式研究的就是这种关系。 -
公式:
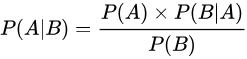
-
解释:
- P(A|B)为后验概率,即指事件B发生的条件下事件A发生的概率,因为该概率得自于B的取值而称为A的后验概率。
- P(A)为先验概率(边缘概率),即A的发生不用考虑B的任何方面的因素。
- P(B|A)为条件概率(类条件概率密度),即指在事件A发生的条件下事件B发生的概率,和1一样被称为B的后验概率。
—>称为似然 - P(B)为”用于归一化的证据因子(evidence)“可以当成一个已知的量,在贝叶斯分类器种P(B)的值与分类无关。
-
-
正态分布(高斯分布):

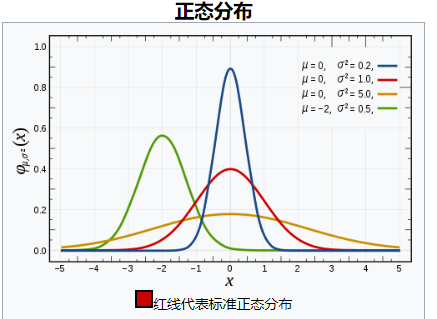
-
多源正态分布:
- 个人理解:将二分类的高斯分布扩展为多个分类的问题。定义详见:https://www.cnblogs.com/bingjianing/p/9117330.html
- 包含了标准化、归化等过程。
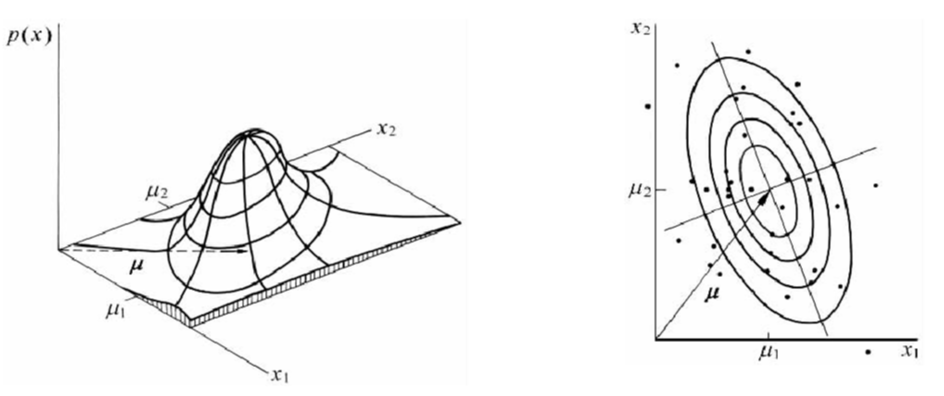
左图为多源高斯分布示意 右图为多远高斯分布的归化过程
(以上为先导概率论知识)
贝叶斯分类器
-
贝叶斯决策论:
- 前提:所有相关概率已知
- 关注点:误判损失
-
期望损失(风险):在N种可能的标记种,λij是指将Cj误分为Ci时所产生的损失。基于后验概率:
P(ci|x)得到误分为Ci时所产生的期望损失,这个损失也叫做”风险“,当我们制定一个准则h使得对于每一个样本x风险最小时(此时整个样本的总体风险R(h*)(贝叶斯风险)也达到最小),称h为贝叶斯最优分类器。
期望损失(风险)表达式
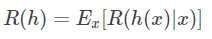
总体风险表达式
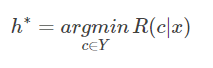
使每个样本的风险最小
-
后验概率最大化与风险最小化:对于二分类问题,λ要么等于0要么等于1
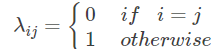
-
此时所以条件风险(该条件下的风险)为
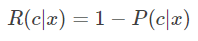
-
所以当分类错误率达到最小时,需要后验概率P最小,继而使后验概率最大化就是使风险最小化。即:
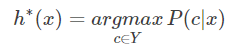
-
-
由3和贝叶斯公式得到,想获得最小风险需要获得最大的后验概率,想获得最大的后验概率需要获得最大的似然。以此引导出——>最大似然估计。
最大似然估计(Maximum Likelihood Estimation)
-
首先,我们的目标是:
P(x|c)这一似然概率,根据频率学派的观点:参数虽然未知,当存在客观的固定值。
我们假设似然概率被一个确定的θc控制,你那么我们的目标就是通过训练集来确定θ c的值,从而确定似然概率的值。
-
假设Dc表示训练集D上的第c类样本的集合,他们满足条件:样本服从独立分布,则参数θc对于数据集Dc的似然可以表示为:
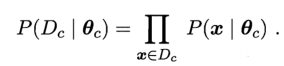
形如:P(A|B)=P(AB)/P(B)
两边取对数(对数似然):
此时,θc最大时的最大似然估计表达式为:
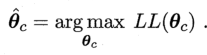
不足:该方法严重依赖假设:存在客观的固定值。
-
MLE估计结果的有偏和无偏性:
- 对于均值:无偏
- 对于反差:有偏,1/n要改为1/(n-1)
-
最大似然估计在样本不足的情况下会出现一个问题:假设我抛10次硬币,有7次是正面朝上,那么我的最大似然估计的概率就是0.7,但是根据常识我们的概率应该靠近0.5才对,这里就需要考虑先验概率。——>引出最大后验概率估计。
最大后验概率(Maximum a posteriori estimation)
-
MAP和MLE的区别:最大似然估计是求参数θ, 使似然函数P(x|θ)最大。最大后验概率估计则是想求θ使P(x|θ)P(θ)最大。求得的θ不单单让似然函数大,θ自己出现的先验概率也得大。
-
MAP的基本思想仍然是基于贝叶斯公式本身,MLE的目的是求出最大的似然估计值,而MAP的目的是求出最大的后验概率本身,在MLE的基础上加上了一个先验概率,他的表达式为:
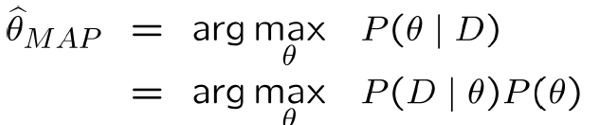
-
主要区别在于贝叶斯学派和频率学派的区别。
朴素贝叶斯分类器
- 引导:
- 如果有d个样本,每个样本有2种状态0或1,
维度为k????,那么他们的组合有2^dk-1种,但是当所有条件独立时,他们的结果有(2-1)dk-1种,使得参数大大减少。 - 所以,在该条件成立之上的朴素贝叶斯之所以叫做”朴素“是因为他需要满足”所有条件独立“这个条件。
- 如果有d个样本,每个样本有2种状态0或1,
- 朴素贝叶斯分类器所依赖的概率模型就是MAP和MLE。
- 应用:文本分类/垃圾邮件筛选等。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号