TJOI2015 day2解题报告
TJOI2015终于写完啦~~~
T1:[TJOI2015]旅游
描述:(BZ没题面只能口述了。。)一个人在一棵树上走,每次从a->b会进行一次贸易(也就是在这条路径上买入物品然后在后面卖出)然后每次经过一个点该点的物品价格会上涨v,求每次贸易的最大获利
很裸的一道树链剖分,就是题目描述太不明白了。。这样就是在某条路径上找到某个点减去后面路径的最小点的值的最大值。可以用线段树的区间合并解决。就是在求答案时的合并答案上方向搞反了查了很久。。。以前也犯过着种错误,以后不能再犯了。。
CODE:

1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<algorithm> 5 #include<vector> 6 using namespace std; 7 #define maxn 50010 8 vector<int> e[maxn]; 9 #define pb push_back 10 int add[maxn],pre[maxn],fa[maxn],pos[maxn]; 11 int n; 12 inline void bfs() { 13 static int q[maxn],s[maxn],ch[maxn]; 14 q[1]=1; 15 for (int l=1,r=1,u=q[l];l<=r;u=q[++l]) 16 for (int i=0;i<e[u].size();i++) 17 if (e[u][i]!=fa[u]) { 18 fa[e[u][i]]=u; 19 q[++r]=e[u][i]; 20 } 21 for (int i=n,u=q[n];i;u=q[--i]) { 22 s[u]++; 23 s[fa[u]]+=s[u]; 24 ch[fa[u]]=s[ch[fa[u]]]<s[u]?u:ch[fa[u]]; 25 } 26 int cnt=0; 27 for (int i=1,u=q[1];i<=n;u=q[++i]) { 28 if (add[u]!=0) continue; 29 pos[add[u]=++cnt]=u;pre[u]=u; 30 for (u=ch[u];u;u=ch[u]) { 31 pos[add[u]=++cnt]=u;pre[u]=pre[fa[u]]; 32 } 33 } 34 } 35 typedef long long ll; 36 struct b { 37 ll mx,mn,ans[2]; 38 b() {mx=mn=ans[0]=ans[1]=0;} 39 }; 40 inline b update(b l,b r) { 41 b ans; 42 ans.mx=max(l.mx,r.mx); 43 ans.mn=min(l.mn,r.mn); 44 ans.ans[0]=max(max(l.ans[0],r.ans[0]),l.mx-r.mn); 45 ans.ans[1]=max(max(l.ans[1],r.ans[1]),r.mx-l.mn); 46 return ans; 47 } 48 inline b rec(b x) { 49 swap(x.ans[0],x.ans[1]); 50 return x; 51 } 52 struct node { 53 int l,r,lz;b bo; 54 }t[maxn*8]; 55 #define lc (x<<1) 56 #define rc (lc^1) 57 #define mid ((l+r)>>1) 58 int a[maxn]; 59 void build(int x,int l,int r){ 60 t[x].l=l,t[x].r=r; 61 if (l==r) { 62 t[x].bo.mx=t[x].bo.mn=a[pos[l]]; 63 t[x].bo.ans[0]=t[x].bo.ans[1]=0; 64 return ; 65 } 66 build(lc,l,mid);build(rc,mid+1,r); 67 t[x].bo=update(t[lc].bo,t[rc].bo); 68 } 69 inline void pb(int x) { 70 if (t[x].lz==0) return ; 71 if (t[x].l!=t[x].r) { 72 t[lc].lz+=t[x].lz; 73 t[lc].bo.mn+=t[x].lz; 74 t[lc].bo.mx+=t[x].lz; 75 t[rc].lz+=t[x].lz; 76 t[rc].bo.mn+=t[x].lz; 77 t[rc].bo.mx+=t[x].lz; 78 } 79 t[x].lz=0; 80 } 81 inline b change(int x,int x1,int y1,int z) { 82 int l=t[x].l,r=t[x].r; 83 pb(x); 84 if (x1<=l&&r<=y1) { 85 t[x].lz+=z; 86 t[x].bo.mn+=z; 87 t[x].bo.mx+=z; 88 return t[x].bo; 89 } 90 b ans; 91 if (mid>=y1) ans=change(lc,x1,y1,z); 92 else if (mid<x1) ans=change(rc,x1,y1,z); 93 else ans=update(change(lc,x1,y1,z),change(rc,x1,y1,z)); 94 t[x].bo=update(t[lc].bo,t[rc].bo); 95 return ans; 96 } 97 inline b set(int x,int y,int z) { 98 int c[2]={x,y}; 99 b ans[2]; 100 bool bo[2]={0,0}; 101 while (c[0]!=c[1]) { 102 int l=add[c[1]]<add[c[0]]?0:1; 103 if (pre[c[l]]==pre[c[l^1]]) { 104 if (bo[l]) ans[l]=update(change(1,add[c[l^1]]+1,add[c[l]],z),ans[l]); 105 else ans[l]=change(1,add[c[l^1]]+1,add[c[l]],z); 106 c[l]=c[l^1]; 107 } else { 108 if (bo[l]) ans[l]=update(change(1,add[pre[c[l]]],add[c[l]],z),ans[l]); 109 else ans[l]=change(1,add[pre[c[l]]],add[c[l]],z); 110 c[l]=fa[pre[c[l]]]; 111 } 112 bo[l]=1; 113 } 114 b _ans=change(1,add[c[0]],add[c[0]],z); 115 if (bo[0]) _ans=update(rec(ans[0]),_ans); 116 if (bo[1]) _ans=update(_ans,ans[1]); 117 return _ans; 118 } 119 int main(){ 120 freopen("travel.in","r",stdin); 121 freopen("travel.out","w",stdout); 122 scanf("%d",&n); 123 for (int i=1;i<=n;i++) scanf("%d",a+i); 124 for (int i=1;i<n;i++) { 125 int x,y; 126 scanf("%d%d",&x,&y); 127 e[x].pb(y);e[y].pb(x); 128 } 129 bfs(); 130 build(1,1,n); 131 int Q; 132 scanf("%d",&Q); 133 while (Q--) { 134 int x,y,v; 135 scanf("%d%d%d",&x,&y,&v); 136 b ans=set(x,y,v); 137 printf("%d\n",ans.ans[1],ans.ans[1],ans.mx,ans.mn); 138 } 139 return 0; 140 }
T2:[TJOI2015]棋盘
就是一道状态压缩+矩阵乘法。
首先我们可以先状压一下,可以发现每次的转移都是相同的,然后就能用矩阵乘法优化了
CODE:

1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 typedef unsigned int uint; 7 struct mat{ 8 uint t[64][64]; 9 mat(){memset(t,0,sizeof(t));} 10 }d,I; 11 int m,n,p,k,w,a[24][24]; 12 mat operator *(mat x,mat y) { 13 mat ans; 14 for (int i=0;i<m;i++) 15 for (int j=0;j<m;j++) 16 for (int k=0;k<m;k++) 17 ans.t[i][j]+=x.t[i][k]*y.t[k][j]; 18 return ans; 19 } 20 mat operator ^ (mat x,int y) { 21 mat ans=I; 22 for (;y;y>>=1) { 23 if (y&1) ans=ans*x; 24 x=x*x; 25 } 26 return ans; 27 } 28 inline bool check(int x,int y){ 29 static bool b[2][24]; 30 memset(b,0,sizeof(b)); 31 for (int i=0;i<w;i++) b[0][i]=x&(1<<i); 32 for (int i=0;i<w;i++) b[1][i]=y&(1<<i); 33 for (int i=0;i<2;i++) 34 for (int j=0;j<w;j++) { 35 if (!b[i][j]) continue; 36 for (int u=0;u<3;u++) 37 for (int v=0;v<p;v++) 38 if (a[u][v]&&(u!=1||v!=k)) { 39 int x=i+u-1,y=j+v-k; 40 if (x>=0&&x<2&&y>=0&&y<w&&b[x][y]) return 0; 41 } 42 } 43 return 1; 44 } 45 int main(){ 46 freopen("chessboard.in","r",stdin); 47 freopen("chessboard.out","w",stdout); 48 scanf("%d%d%d%d",&n,&w,&p,&k); 49 for (int i=0;i<3;i++) 50 for (int j=0;j<p;j++) scanf("%d",a[i]+j); 51 m=1<<w; 52 for (int i=0;i<m;i++) I.t[i][i]=1; 53 for (int i=0;i<m;i++) 54 for (int j=0;j<m;j++) 55 d.t[i][j]=check(i,j); 56 cout<<(d^n+1).t[0][0]<<endl; 57 return 0; 58 }
这个嘛。。。先贴下官方题解吧


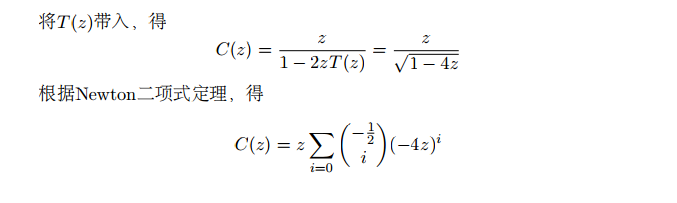

好复杂对吧,我们打个表 。。。
f[1]=1/1,f[2]=3/3,f[3]=6/5,f[4]=10/7 ...
找到了吧 f[n]=n*(n+1)/2/(2n-1)。
完了。。。
CODE:

1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 using namespace std; 6 int main(){ 7 int n; 8 scanf("%d",&n); 9 printf("%.9lf\n",n*1ll*(n+1)/2*1.0/(2*n-1)); 10 return 0; 11 }
话说BZ 350道题了。。。其实这一年几乎都在学校的oj上刷,能在这1年的时间刷多了100道题也挺自豪的。。。想想自己100时的那种兴奋,还是觉得自己挺弱智的。。。
还有3个小时就是自己的17岁生日了,回想自己的第16个年头,还是挺满意的,至少自己坚持了自己的路。在这里祝自己生日快乐,在接下来的一年里会接受越来越大的挑战,或者省队都进不了直接滚粗,或者noi胸牌滚粗,又或者侥幸成为了进队爷。。。不管自己今后咋样,希望能不忘本心吧,自己选择的路,就算跪着也要走完。
距GDOI还有4天,明天就是最后的一场模拟赛了,自己却感觉还总是找不到感觉,真的不想再发生像NOIP还有GDKOI时那黑暗的第二天了。。。自己真的很想被人敬仰膜拜一番,加油吧,再认真仔细一点吧。
以后的路会怎样,就跟我现在在听的歌一样吧。God knows,只有上帝才会知道,我们现在所能做的,只有认真过好每一分每一秒了
GDOI,God Bless!!!



